
Урок «Равносильность уравнений Проверка корней. Потеря корней при решении уравнения»

Краткое описание документа:
На прошлом уроке при решении уравнений мы использовали три этапа.
Первый этап - технический. С помощью цепочки преобразований от исходного уравнения мы приходим к достаточно простому, которое решаем и находим корни.
Второй этап — анализ решения. Анализируем преобразования, которые выполнили, и выясняем, равносильны ли они.
Третий этап – проверка. Проверка всех найденных корней их подстановкой в исходное уравнение обязательна при выполнении преобразований, которые могут привести к уравнению-следствию
Всегда ли нужно выделять три этапа при решении уравнения?
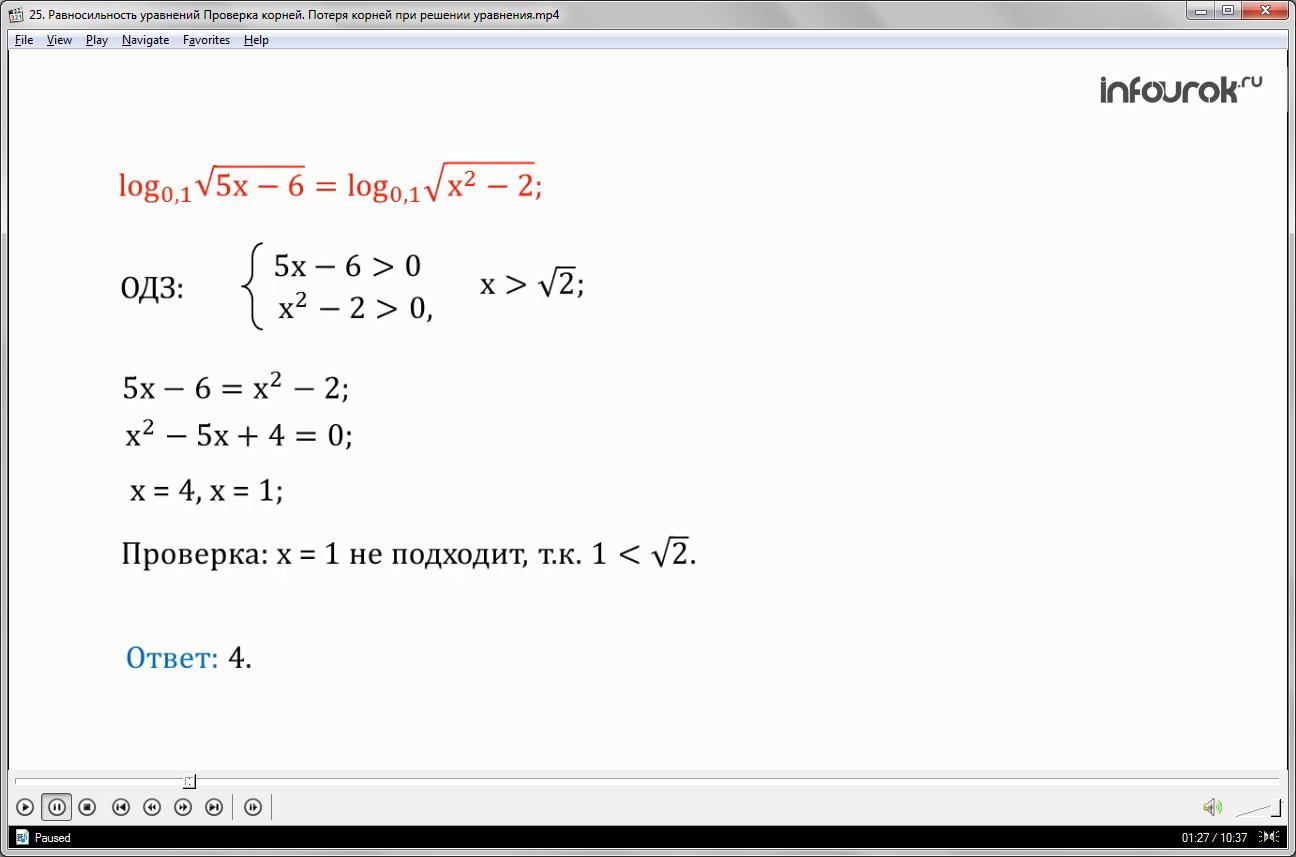
Конечно, нет. Как, например, в решении этого уравнения. В повседневной жизни их обычно не выделяют. Но все эти этапы нужно «держать в голове» и выполнять в той или иной форме. Обязательно проводить анализ на равносильность преобразований. И если анализ показал, что нужно выполнить проверку, то она обязательна. В противном случае уравнение не может считаться решенным верно.
Всегда ли только подстановкой можно выполнить проверку корней уравнения?
Если при решении уравнения использовались равносильные преобразования, то проверка не требуется. При проверке корней уравнения очень часто используют ОДЗ (область допустимых значений).Если по ОДЗ проверку сделать трудно, то выполняют ее подстановкой в исходное уравнение.
Задание 1
Решить уравнение квадратный корень из двух икс плюс три равен одному плюс икс.
Решение
ОДЗ уравнения определяется системой двух неравенств: два икс плюс три больше либо равно нулю и один плюс икс больше либо равно нулю. Решением является икс больше либо равно минус единице.
Возведем обе части уравнения в квадрат, перенесем слагаемые из одной части уравнения в другую, приведем подобные слагаемые, получим квадратное уравнение икс в квадрате равно двум. Корни его —
икс первое, второе равно плюс-минус квадратный корень из двух.
Проверка
Значение икс первое равно квадратный корень из двух является корнем уравнения, так как оно входит в ОДЗ.
Значение икс второе равно минус квадратный корень из двух не является корнем уравнения, т.к. оно не входит в ОДЗ.
Проверим корень икс равно квадратный корень из двух, подставив его в исходное равенство, получим
верное равенство, значит, икс равное квадратному корню из двух является корнем уравнения.
Ответ: квадратный корень из двух.
Задание 2
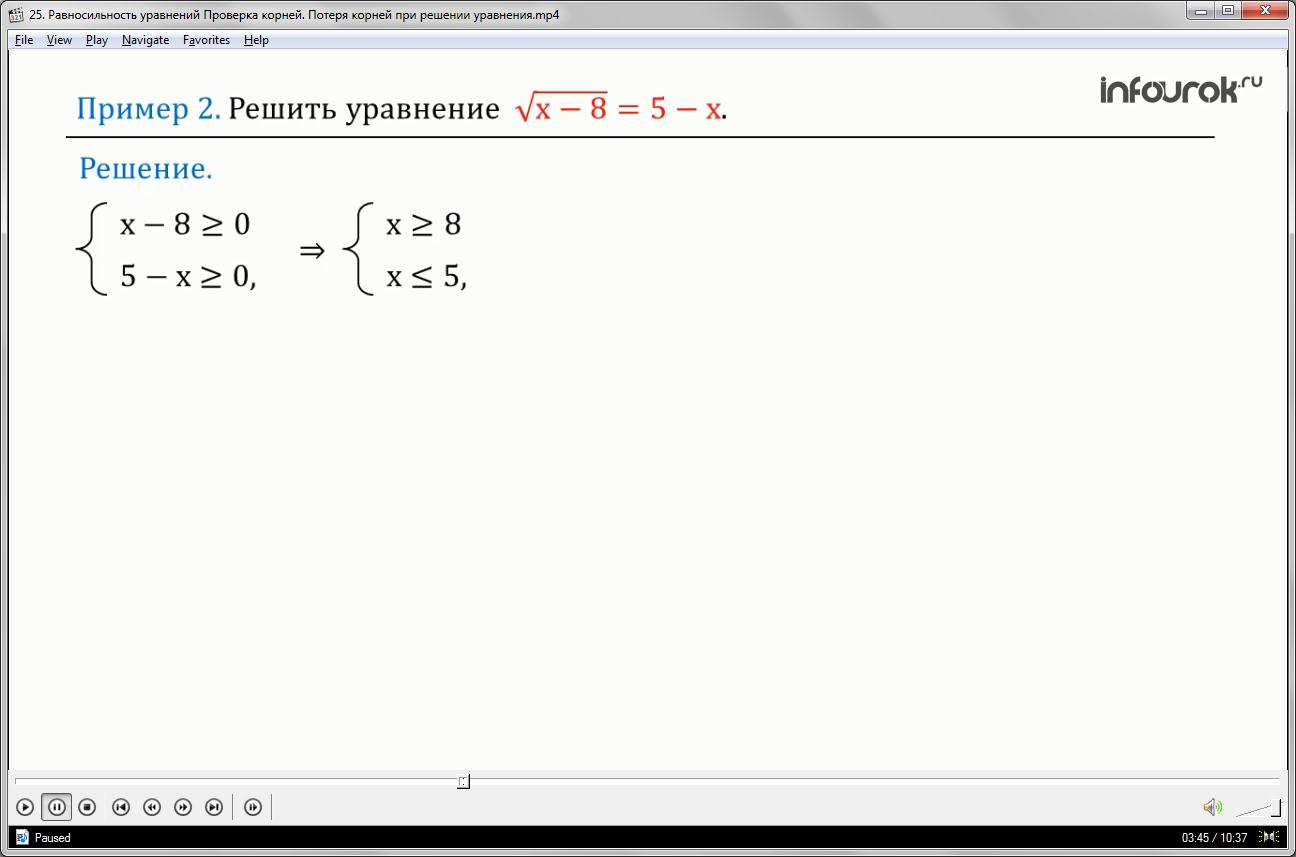
Решить уравнение квадратный корень из икс минус восемь равно пять минус икс.
Решение
ОДЗ иррационального уравнения определяется системой двух неравенств: икс минус восемь больше либо равно нулю и пять минус икс больше либо равно нулю . Решая ее, получаем, что эта система не имеет решений. Корнем уравнения не может быть ни одно из значений переменной икс.
Ответ: корней нет.
Задание 3
Решить уравнение квадратный корень из икс в кубе плюс четыре икс минус один минус восемь квадратных корней из икс в четвертой степени минус икс равно квадратный корень из икс в кубе минус один плюс два квадратных корня из икс.
Решение
Найти ОДЗ в этом уравнении довольно трудно.
Выполним преобразования: возведем обе части этого уравнения в квадрат,
перенесем все слагаемые в левую часть уравнения и приведем подобные слагаемые, два корня запишем под один, получим подобные радикалы, приводим подобные, делим на коэффициент минус 12, и раскладываем подкоренное выражение на множители, получим уравнение в виде произведения двух множителей, равное нулю. Решив его, найдем корни:
икс первое равно единице, икс второе равно нулю.
Так как мы обе части уравнения возводили в четную степень, то проверка корней обязательна.
Проверка
Если икс равен единице, то
получим верное равенство, значит, икс равный единице – корень уравнения.
Если икс равен нулю, то квадратный корень из минус единицы не определен.
Значит, икс равный нулю – посторонний корень.
Ответ: один.
Задание 4
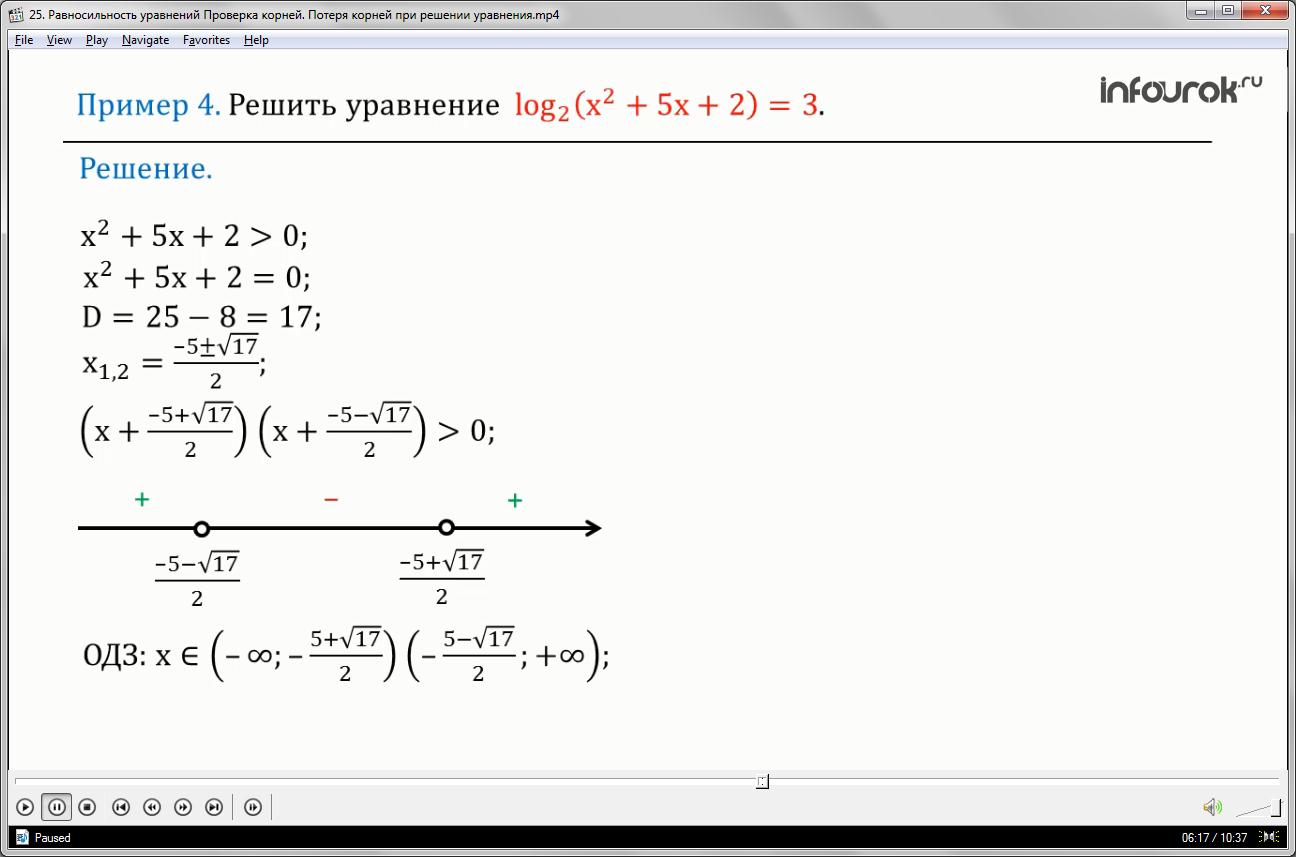
Решить уравнение логарифм выражения икс квадрат плюс пять икс плюс два по основанию два равно трем.
Решение
Найдем ОДЗ уравнения. Для этого решим неравенство икс квадрат плюс пять икс плюс два больше нуля.
Решаем неравенство методом интервалов. Для этого разложим его левую часть на множители, предварительно решив квадратное уравнение, и учитывая знак неравенства, определяем ОДЗ. ОДЗ равно объединению открытых лучей от минус бесконечности до минус дроби пять плюс квадратный корень из семнадцати, деленное на два, и от минус дроби пять минус квадратный корень из семнадцати, деленное на два, до плюс бесконечности.
Теперь приступим к поиску корней уравнения. Учитывая, что три равно логарифму восьми по основанию два, запишем уравнение в следующем виде: логарифм выражения икс квадрат плюс пять икс плюс два по основанию два равно логарифму восьми по основанию два. Потенцируем уравнение, получим и решим квадратное уравнение.
Дискриминант равен сорока девяти.
Вычисляем корни:
икс первое равно минус шести; икс второе равно единице.
Проверка
Минус шесть принадлежит ОДЗ, единица принадлежит ОДЗ, значит, оба числа являются корнями уравнения.
Ответ: минус шесть; один.
На прошлом уроке мы рассматривали вопрос о появлении посторонних корней. Мы их можем обнаружить с помощью проверки. А можно ли при решении уравнения потерять корни и как этого не допустить?
При выполнении таких действий над уравнением, как, во-первых, деление обеих частей уравнения на одно и то же выражение аш от икс (кроме тех случаев, когда точно известно, что аш от икс не равно нулю при любом икс из области определения уравнения);
во – вторых, сужение ОДЗ уравнения в процессе решения может привести к потере корней уравнения.
Запомните!
Уравнение, записанное в виде
эф от икс умноженное на аш от икс равно жэ от икс умноженное на аш от икс решается таким образом:
нужно разложить на множители вынесением за скобки общего множителя;
затем, каждый множитель приравнять к нулю, тем самым получим два уравнения.
Вычисляем их корни.
Задание 1
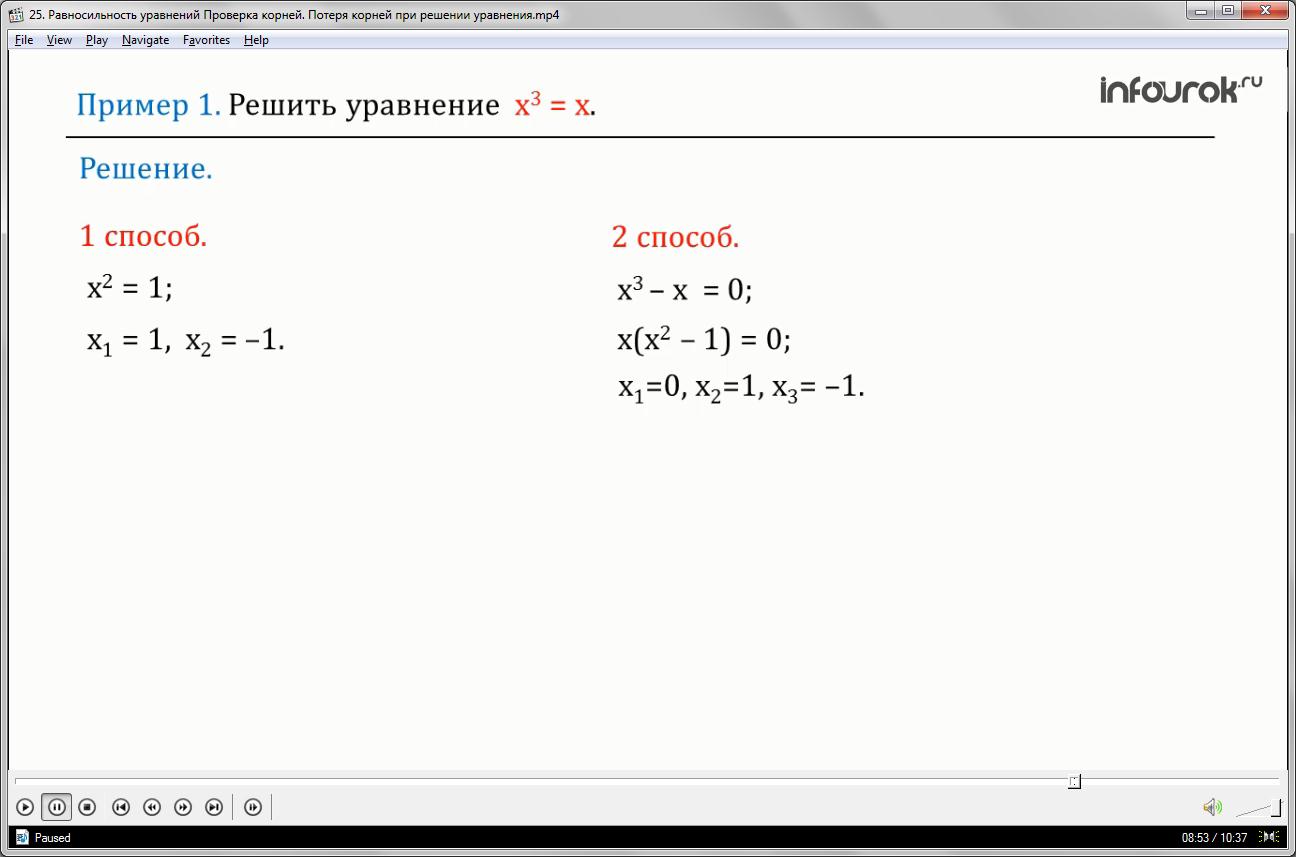
Решить уравнение икс куб равно икс.
Первый способ
Разделим обе части данного уравнения на икс, получим икс квадрат равно единице, имеющее корни икс первое равно единице,
икс второе равно минус единице.
Второй способ
Икс куб равно икс. Перенесем икс в левую часть уравнения, вынесем икс за скобки, получим: икс, умноженное на икс квадрат, минус один равно нулю.
Вычислим его корни:
Икс первое равно нулю, икс второе равно единице, икс третье равно минус единице.
Уравнение имеет три корня.
При решении первым способом мы потеряли один корень — икс равно нулю.
Ответ: минус один; ноль; один.
Запомните! Сокращение обеих частей уравнения на множитель, содержащий неизвестное, может привести к потере корней.
Задание 2
Решить уравнение десятичный логарифм икс в квадрате равен двум.
Решение
Первый способ
По определению логарифма, получим квадратное уравнение икс квадрат равно сто.
Его корни: икс первое равно десяти; икс второе равно минус десяти.
Второй способ
По свойству логарифма имеем два десятичных логарифма икс равно двум.
Его корень — икс равен десяти
При втором способе произошла потеря корня икс равен минус десяти. А причина в том, что применили неправильную формулу, сужающую область определения уравнения. Выражение десятичный логарифм икс в квадрате определено для всех икс, кроме икс равное нулю. Выражение десятичный логарифм икс — для икс больше нуля. Правильная формула десятичный логарифм икс квадрат равен двум десятичным логарифмам модуль икс.
Запомните! При решении уравнения грамотно применяйте имеющиеся формулы.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8980 |
| Номер материала | 1074 |