
Урок «Равносильность уравнений. Уравнение %U2013 следствие»

Краткое описание документа:
Для изучения сегодняшней темы нам необходимо повторить, какое уравнение называется уравнением-следствием, какие теоремы «беспокойные» и из каких этапов состоит решение любого уравнения.
Определение.Если каждый корень уравнения эф от икс равно же от икс (обозначим его цифрой один) является в то же время корнем уравнения пэ от икс, равное аш от икс (обозначим его цифрой два), то уравнение два называют следствием уравнения один.
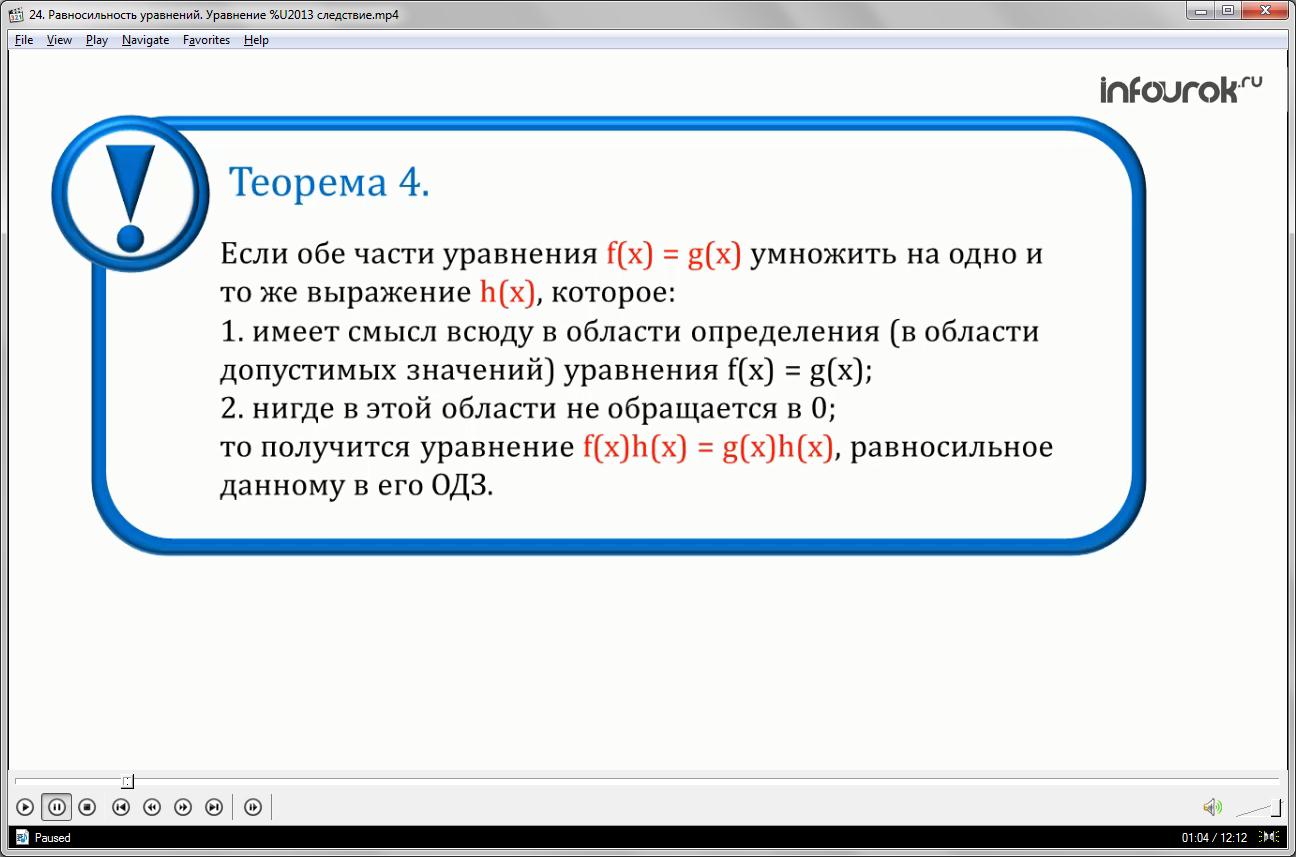
Теорема четвертая. Если обе части уравнения эф от икс равно же от иксумножить на одно и то же выражение аш от икс, которое:
Во- первых, имеет смысл всюду в области определения (в области допустимых значений) уравнения эф от икс, равное же от икс.
Во-вторых, нигде в этой области не обращается в нуль, то получится уравнение эф от икс, умноженное на аш от икс равно же от икс, умноженное на аш от икс, равносильное данному в его ОДЗ.
Следствием теоремы четыре является еще одно «спокойное» утверждение: если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Теорема пятая. Если обе части уравнения
эф от икс равно же от икснеотрицательны в ОДЗ уравнения, то после возведения обеих его частей в одну и ту же четную степень n получится уравнение эф от икс в энной степени равно же от иксв энной степени равносильное данному уравнению в его о дэ зэ.
Теорема шестая. Пусть а больше нуля, а не равное единице, и эф от икс больше нуля,
жэ от икс больше нуля,тологарифмическое уравнение логарифм эф от икс по основанию а, равное логарифму жэ от икс по основанию а,
равносильно уравнению эф от икс равно же от икс.
Как мы уже говорили, решение любых уравнений происходит в три этапа:
Первый этап — технический. С помощью цепочки преобразований от исходного уравнения мы приходим к достаточно простому уравнению, которое решаем и находим корни.
Второй этап — анализ решения. Анализируем преобразования, которые выполнили, и выясняем, равносильны ли они.
Третий этап — проверка. Проверка всех найденных корней их подстановкой в исходное уравнение обязательна при выполнении преобразований, которые могут привести к уравнению-следствию.
На этом уроке мы выясним, при применении каких преобразований данное уравнение переходит в уравнение-следствие? Рассмотрим следующие задания.
Задание 1
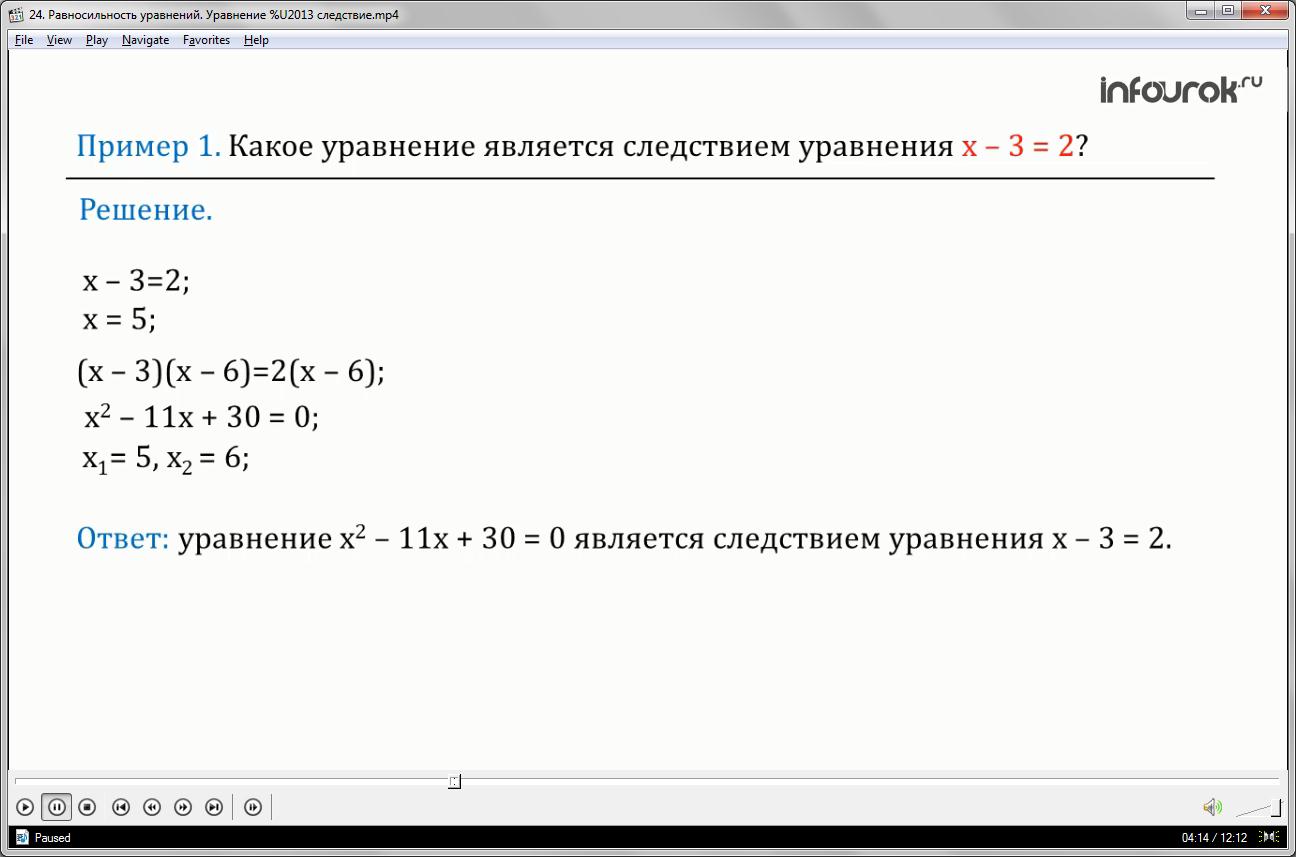
Какое уравнение является следствием уравнения икс минус три равно двум?
Решение
Уравнение икс минус три равно двум имеет единственный корень — икс равно пяти. Умножим обе части этого уравнения на выражение икс минус шесть, приведем подобные слагаемые и получим квадратное уравнение икс квадрат минус одиннадцать икс плюс тридцать равно нулю. Вычислим его корни: икс первое равно пяти; икс второе равно шести. Оно уже содержит два корня. Уравнение икс квадрат минус одиннадцать икс плюс тридцать равно нулю содержит единственный корень — икс равно пяти; уравнения икс минус три равно двум, поэтому икс квадрат минус одиннадцать икс плюс тридцать является следствием уравнения икс минус три равно двум.
Задание 2
Какое еще уравнение является следствием уравнения х-3=2?
Решение
В уравнении икс минус три равно двум возведем в квадрат его обе части, применим формулу квадрата разности, приведем подобные слагаемые, получим квадратное уравнение икс квадрат минус шесть икс плюс пять равно нулю.
Вычислим его корни: икс первое равно пяти, икс второе равно единице.
Корень икс равно единице является посторонним для уравнения икс минус три равно двум. Это получилось потому, что обе части исходного уравнения возвели в квадрат (четная степень). Но при этом его левая часть — икс минус три — может быть отрицательной (нарушены условия теоремы пять). Значит, уравнение икс квадрат минус шесть икс плюс пять равно нулю является следствием уравнения икс минус три равно двум.
Задание 3
Найти уравнение-следствие для уравнения
логарифм выражения икс плюс один по основанию три плюс логарифм выражения икс плюс три по основанию три равно единице.
Решение
Представим единицу как логарифм трех по основанию три, потенцируем логарифмическое уравнение, выполним умножение, приведем подобные слагаемые и получим квадратное уравнение икс квадрат плюс четыре икс равно нулю. Вычислим его корни: икс первое равно нулю, икс второе равно минус четырем. Корень икс равно минус четырем является посторонним для логарифмического уравнения, так как при подстановке его в логарифмическое уравнение выражения икс плюс один и икс плюс три принимают отрицательные значения — нарушены условия теоремы шесть.
Значит, уравнение икс квадрат плюс четыре икс равно нулю является следствием данного уравнения.
На основании решения этих примеров, мы можем сделать вывод: уравнение-следствие получается из данного уравнения путем расширения области определения уравнения. А это возможно при выполнении таких преобразований, как
1)избавление от знаменателей, содержащих переменную величину;
2)возведение обеих частей уравнения в одну и ту же четную степень;
3)освобождение от знаков логарифмов.
Запомните!Если в процессе решения уравнения произошло расширение области определения уравнения, то обязательна проверка всех найденных корней.
Задание 4
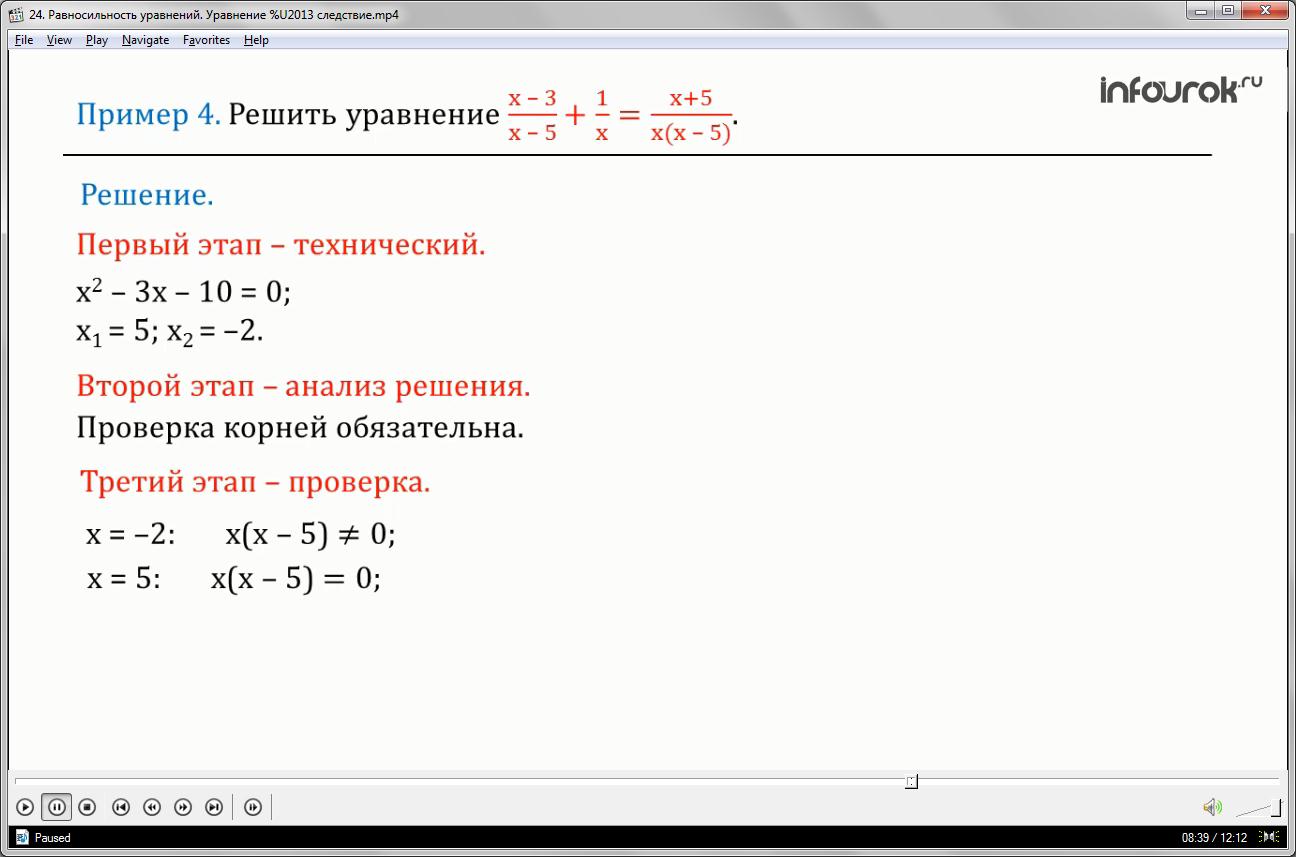
Решить уравнение икс минус три, деленное на икс минус пять, плюс один, деленное на икс, равно икс плюс пять, деленное на икс, умноженное на икс минус пять.
Решение
Первый этап - технический.
Выполним цепочку преобразований, получим наиболее простое уравнение и решим его. Для этого умножим обе части уравнения на общий знаменатель дробей, то есть на выражение икс умноженное на иксминус пять.
Получим квадратное уравнение икс квадрат минус три икс минус десять равно нулю. Вычислим корни: икс первое равно пяти, икс второе равно минус двум.
Второй этап– анализ решения.
Проверим выполненные преобразования на равносильность.
При решении уравнения, мы его обе части умножили на выражение, содержащее переменную. Значит, область определения уравнения расширилась. Поэтому проверка корней обязательна.
Третий этап – проверка.
Подставим найденные корни в исходное уравнение.
При икс равном минусдваобщийзнаменатель не обращается в нуль. Значит, икс равно минусдваявляется корнем данного уравнения.
При икс равном пяти общий знаменатель обращается в нуль. Поэтому икс равно пяти – посторонний корень.
Ответ: минус два.
Задание 5
Решить уравнение квадратный корень из икс минус шесть равно квадратному корню из четырех минус икс.
Решение
Первый этап — технический.
Для того чтобы получить простое уравнение и решить его, выполним цепочку преобразований.
Возведем в квадрат (четная степень) обе части этого уравнения, перенесем иксы в левую часть , а числа в правую часть уравнения, приведем подобные слагаемые, получим: два икс равно десяти. Икс равен пяти.
Второй этап– анализ решения.
Проверим выполненные преобразования на равносильность.
При решении уравнения, мы его обе части возвели в квадрат. Значит, область определения уравнения расширилась. Поэтому проверка корней обязательна.
Третий этап – проверка.
Подставим найденные корни в исходное уравнение.
Если икс равен пяти, выражение квадратный корень из четырех минус икс не определено, поэтому икс, равный пяти – посторонний корень. Значит, данное уравнение не имеет корней.
Ответ: уравнение корней не имеет.
Задание 6
Решить уравнение натуральный логарифм выражения икс квадрат плюс два икс минус семь равно натуральному логарифму выражения икс минус один.
Решение
Первый этап — технический.
Выполним цепочку преобразований, получим наиболее простое уравнение и решим его. Для этого потенцируем
уравнение, перенесем все слагаемые в левую часть уравнения, приведем подобные члены, получим квадратное уравнение икс квадрат плюс икс минус шесть равно нулю. Вычислим корни: икс первое равно двум, икс второе равно минус трем.
Второй этап – анализ решения.
Проверим выполненные преобразования на равносильность.
В процессе решения данного уравнения мы освободились от знаков логарифмов. Значит, область определения уравнения расширилась. Поэтому проверка корней обязательна.
Третий этап – проверка.
Подставим найденные корни в исходное уравнение.
Если икс равен двум, то получаем натуральный логарифм единицы равен натуральному логарифму единицы —
верное равенство.
Значит, икс равный двум – корень данного уравнения.
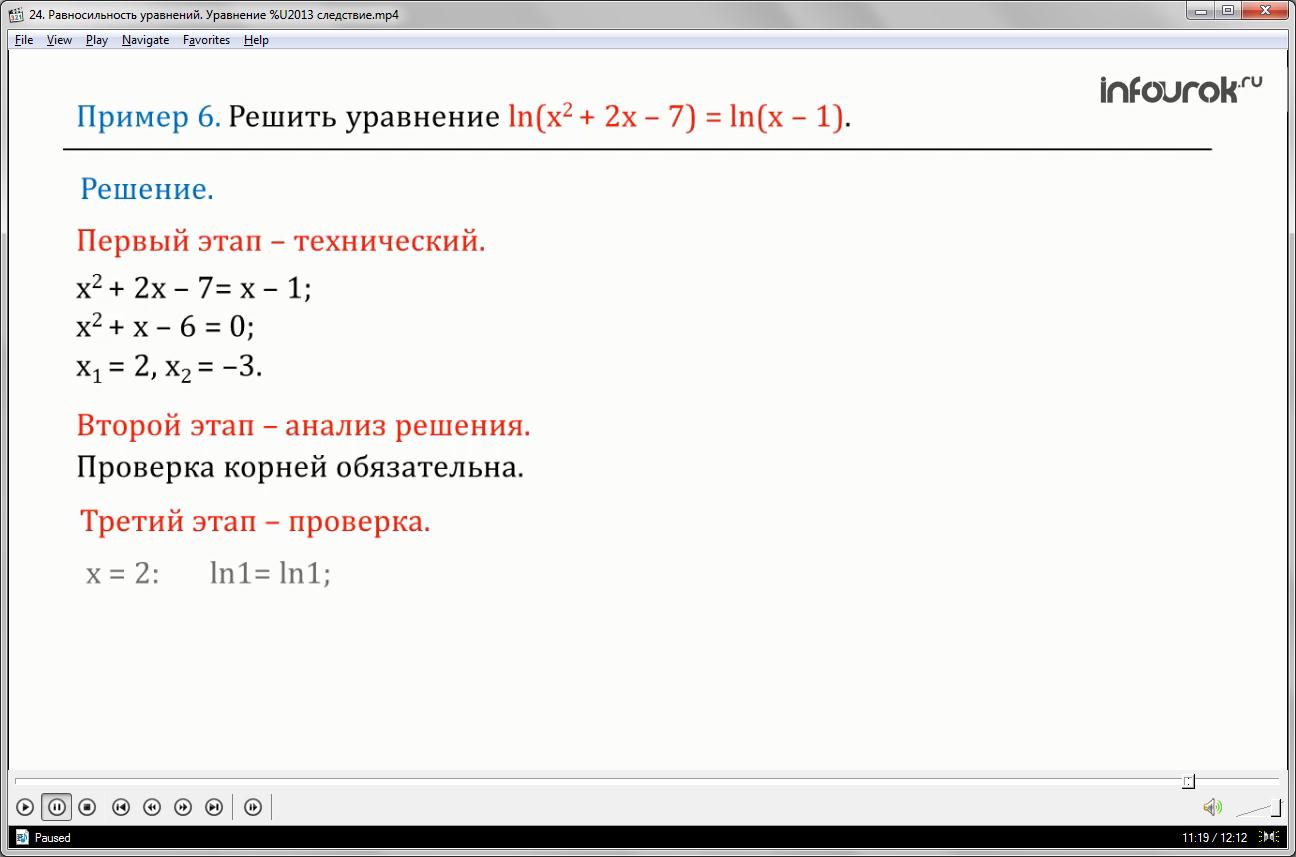
Если икс равен минус трем, то натуральный логарифм выражения икс квадрат плюс два икс минус семь и натуральный логарифм выражения икс минус один не определены. Значит, икс равный минус трем — посторонний корень.
Ответ: два.
Всегда ли нужно при решении уравнения выделять три этапа? Каким еще способом можно выполнить проверку?
Ответы на эти вопросы мы получим на следующем уроке.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5173 |
| Номер материала | 1073 |