
Урок «Разложение квадратного трехчлена на множители»

Краткое описание документа:
Данная тема изучается в системе уроков, связанных с многочленами, в курсе алгебры 9 класса. материал по теме «Разложение квадратного трехчлена на множители» позволит в дальнейшем быстрее и рациональнее решать задачи и упражнения.

Урок рассчитан на 6:12 минут. За это время автор успевает достаточно полно и подробно рассказать материал, подкрепив его примерами.
Как раз начинается урок с рассмотрения примера. Для начала автор замечает, что в данном выражении можно вынести за скобки общий множитель. Затем он применяет способ группировки и раскладывает многочлен на множители. В ходе решения данного примера была выявлена закономерность между конечным разложением трехчлена на множители и его корнями. Получается, что для того, чтобы разложить квадратный трехчлен на множители, достаточно найти его корни и записать разложение.
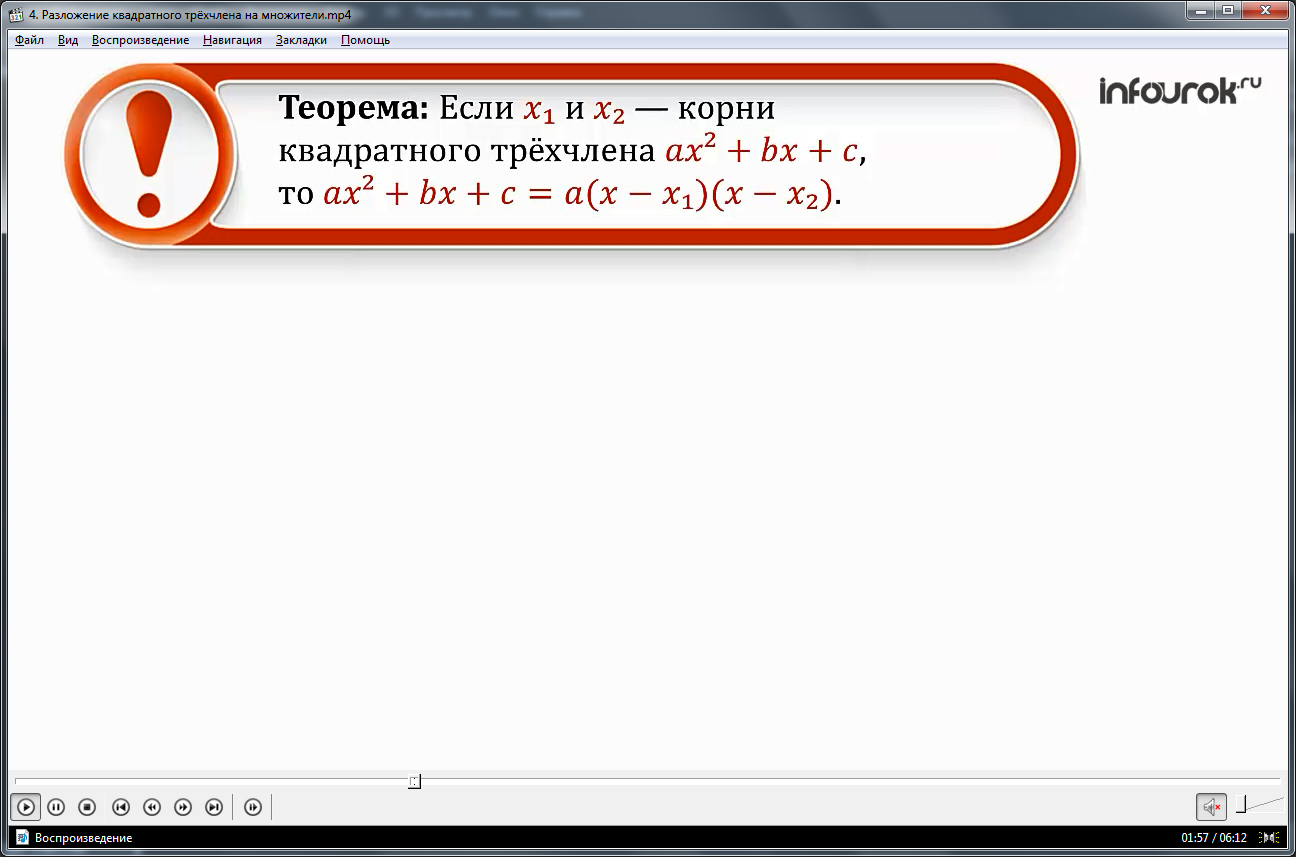
Затем автор замечает, что когда дискриминант квадратного трехчлена равен нулю, то трехчлен имеет два одинаковых корня. После этого вводится теорема, которая связывает корни квадратного трехчлена и разложение его на множители. И здесь же на экране проводится подробное доказательство этой теоремы. Автор подробно и четко ведет доказательство, при этом поясняя каждый необходимый момент.

Когда теорема доказана, автор знакомит слушателей с замечанием. В нем говорится о том, что трехчлен, не имеющий корней, нельзя разложить на множители. Это замечание доказывается. Как обычно, доказательство ведется подробно и с пояснениями. Доказательство этого замечания строится методом от противного. Предполагается, что такое разложение имеет место быть. Но в ходе доказательства автор приходит к тому, что у квадратного трехчлена есть корни. Но по условию трехчлен корней не имеет. Значит, вывод один: нельзя такой трехчлен разложить на множители.
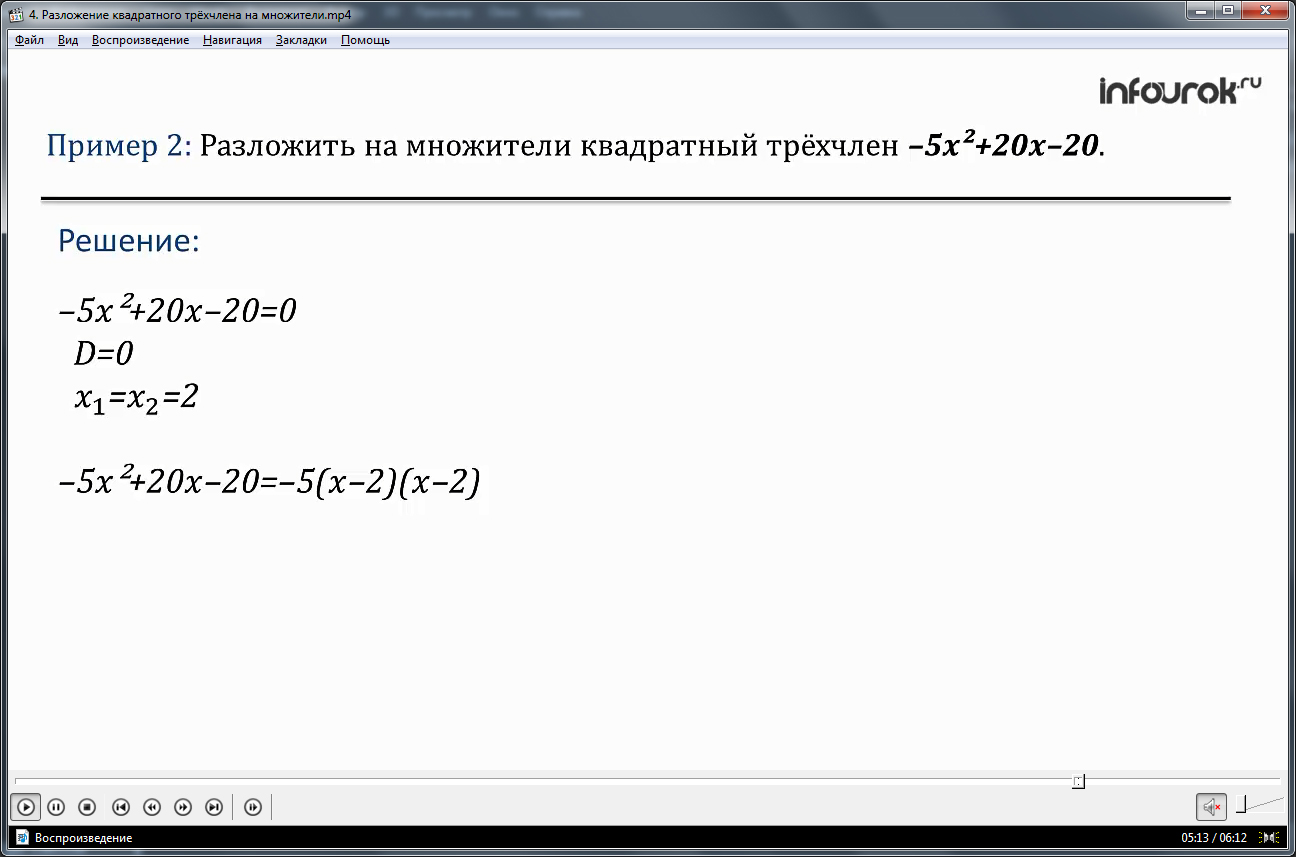
Далее следует пример, который показывает, как применяются только что полученные знания. Автор раскладывает на множители трехчлен. А для этого он находит его корни. Так как трехчлен имеет два различных корня, то его разложение имеет тот вид, о котором говорилось выше. Следующий пример показывает другое разложение, когда трехчлен имеет два одинаковых корня.
Третий пример наглядно демонстрирует, где и как можно применить правило разложения квадратного трехчлена на множители, которое только что было изучено. А именно, дана алгебраическая дробь, которую требуется сократить. Если в ее первоначальном виде сократить невозможно, то после того, как трехчлен, записанный в знаменателе, разложен на множители, появляется возможность сократить преобразованную дробь. На этом урок заканчивается. Остается только подобрать задания для закрепления.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 4408 |
| Номер материала | 675 |