
Урок «Решение неравенств с одной переменной»

Краткое описание документа:
Для изучения сегодняшней темы нам необходимо вспомнить, что называется решением неравенства эф от икс больше жэ от икс.
Значение переменной икс, при котором данное неравенство с переменной обращается в верное числовое неравенство, называется решением неравенства эф от икс больше жэ от икс.
Иногда его называют частным решением.
Множество всех частных решений дает нам общее решение. Но чаще этот термин опускают и говорят просто — решение.
Определение1
Два неравенства с одной переменной эф от икс больше жэ от икс и пэ от икс больше аш от икс называются равносильными, если их решения совпадают.
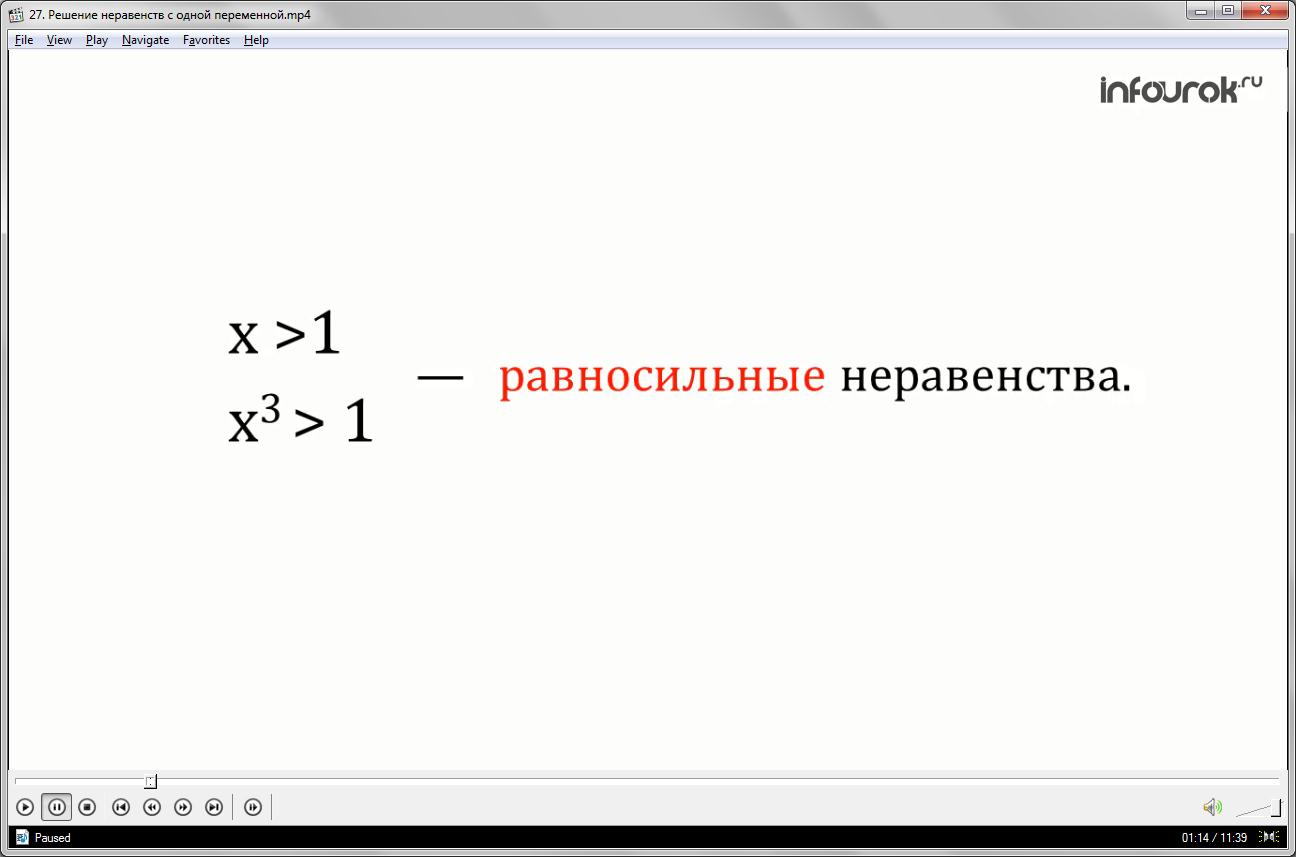
Например, неравенства икс больше одного и икс куб больше одного являются равносильными на множестве всех действительных чисел, поэтому говорят, что они равносильны.
Определение 2.
Если решение неравенства эф от икс больше жэ от икс (обозначим номером один) содержится в решении неравенства пэ от икс больше аш от икс (обозначим номером два), то неравенство второе называют следствием неравенства первого.
Решением неравенства икс минус три больше нуля является открытый числовой луч от трех до плюс бесконечности.
Решением неравенства логарифм выражения икс минус три по основанию три меньше одного является интервал от трех до шести.
Так как решение неравенства
логарифм выражения икс минус три по основанию три меньше одного содержится в решении икс минус три больше нуля, то неравенство икс минус три больше нуля является следствием неравенства логарифм выражения икс минус три по основанию три меньше одного.
Запомните! При решении неравенств необходимо выполнять только равносильные преобразования. При этом используются шесть теорем равносильности неравенств.
Теорема первая.
Если какой-либо член неравенства перенести из одной части неравенства в другую с противоположным знаком, сохранив знак неравенства, то получится неравенство, равносильное данному.
Например, неравенство икс квадрат минус семь больше либо равно девять икс равносильно неравенству икс квадрат минус девять икс минус семь больше либо равно нулю, так каквыполнили равносильное преобразование: перенесли девять икс с противоположным знаком в левую часть неравенства.
Теорема вторая.
Если обе части неравенства возвести в одну и ту же нечетную степень, оставив знак неравенства без изменения, то получится неравенство, равносильное данному неравенству.
Например, неравенство корень пятой степени из двух икс минус семь больше или равно корень пятой степени из восьми плюс икс равносильно неравенству два икс минус семь больше либо равно восемь плюс икс (обе части возвели в нечетную (пятую) степень).
Теорема третья.
Показательное неравенство а в степени эф от икс больше а в степени жэ от иксравносильно:
1) неравенству того же смысла эф от икс больше жэ от икс, если а больше одного;
2) неравенству противоположного смысла эф от икс меньше а в степени жэ от икс, если а больше нуля и меньше единицы.
Задание 1
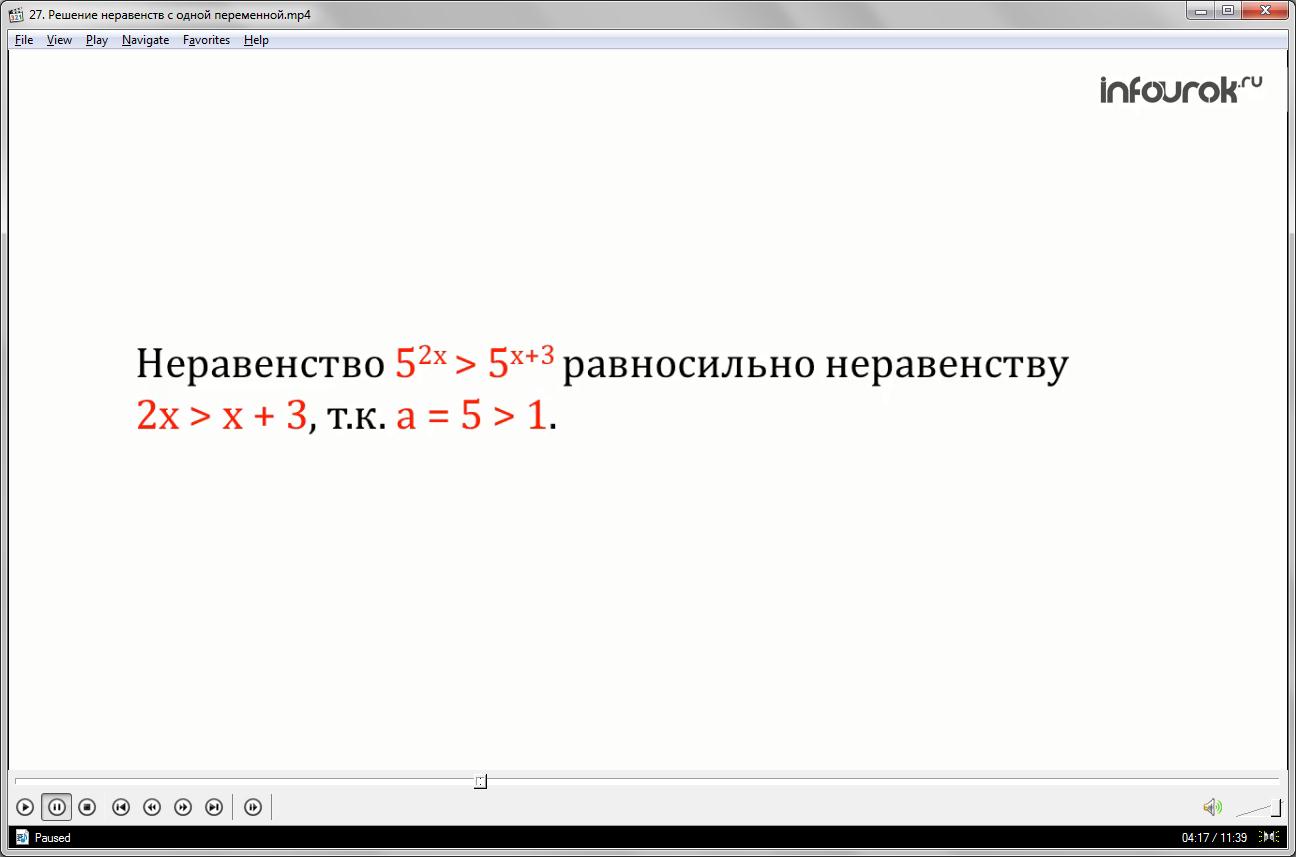
Неравенство пять в степени два икс больше пяти в степени икс плюс три равносильно неравенству два икс больше икс плюс три. Знак неравенства сохранили, так как основание степени равно пяти и больше единицы.
Задание 2
Неравенство ноль целых пять десятых в степени два икс больше нуля целых пяти десятых в степени икс плюс три равносильно неравенству два икс меньше икс плюс три.
Знак неравенства поменяли, так как основание степени равно нулю целым пяти десятым больше нуля и меньше единицы.
Теорема четвертая.
Первое. Если обе части неравенства эф от икс больше жэ от икс умножить на одно и то же выражение аш от икс, положительное при всех икс из области определения (области допустимых значений переменной) неравенства эф от икс больше жэ от икс, оставив при этом знак неравенства без изменения, то получится неравенство эф от икс умноженное на аш от икс больше жэ от икс умноженное на аш от икс, равносильное данному.
Второе. Если обе части неравенства эф от икс больше жэ от икс умножить на одно и то же выражение аш от икс, отрицательное при всех икс из области определения (области допустимых значений переменной) неравенства эф от икс больше жэ от икс, изменив при этом знак неравенства на противоположный , то получится неравенство эф от икс умноженное на аш от икс меньше жэ от икс умноженное на аш от икс, равносильное данному.
Задание 1
Неравенство — дробь, числитель которой — три икс плюс пять, а знаменатель — квадратный корень из квадрата икс плюс два больше дроби, числитель которой — икс минус три, а знаменатель — квадратный корень из квадрата икс плюс два равносильно неравенству три икс плюс пять больше икс минус три (обе части умножили на выражение квадратный корень из квадрата икс плюс два, положительное при всех значениях икс).
Задание 2
Неравенство: дробь, числитель которой — три икс плюс пять, а знаменатель — логарифм выражения икс в квадрате плюс один по основанию ноль целых четыре десятых меньше либо равно дроби, числитель которой — икс минус три, а знаменатель — логарифм выражения икс в квадрате плюс один по основанию ноль целых четыре десятых равносильно неравенству три икс плюс пять больше либо равно икс минус три (обе части умножили на выражение логарифм выражения икс в квадрате плюс один по основанию ноль целых четыре десятых отрицательное при всех значениях икс, и изменили при этом знак неравенства).
Теорема пятая.
Если обе части неравенства эф от икс больше жэ от икс неотрицательны в области его определения, то после возведения в одну и ту же четную степень эн, получится неравенство того же смысла эф от икс в энной степени больше жэ от икс в энной степени, равносильное данному неравенству.
Например, обе части неравенства модуль выражения икс минус четыре больше модуля выражения икс плюс шесть неотрицательны для любых икс. Возведем их в квадрат. Получим неравенство икс минус четыре и все в квадрате больше икс плюс шесть и все в квадрате равносильное данному неравенству. Множество его решений — открытый луч от минус бесконечности до минус единицы и является решением данного неравенства.
Теорема шестая.
Если эф от икс больше нуля и жэ от икс больше нуля, то логарифмическое неравенство логарифм эф от икс по основанию а больше логарифма жэ от икс по основанию а равносильно:
1) неравенству того же смысла эф от икс больше жэ от икс, если а больше единицы;
2) неравенству противоположного смысла
эф от икс меньше а в степени жэ от икс, если а больше нуля и меньше единицы.
Задание 1
Неравенство логарифм выражения три икс минус шесть по основанию четыре больше логарифма выражения два икс плюс четыре по основанию четыре в его ОДЗ икс больше двух равносильно неравенству
три икс минус шесть больше два икс плюс четыре, так как основание логарифма равно четырем больше единицы.
Задание 2
Неравенство логарифм выражения три икс минус шесть по основанию ноль целых четыре десятых больше логарифма выражения два икс плюс четыре по основанию ноль целых четыре десятых в его ОДЗ икс больше двух равносильно неравенству три икс минус шесть меньше два икс плюс четыре, так как основание логарифма равно ноль целых четыре десятых больше нуля и меньше единицы.

Обратите внимание! При решении неравенства следует учитывать условия применимости теорем. В противном случае возможны грубые ошибки.
Задание 3
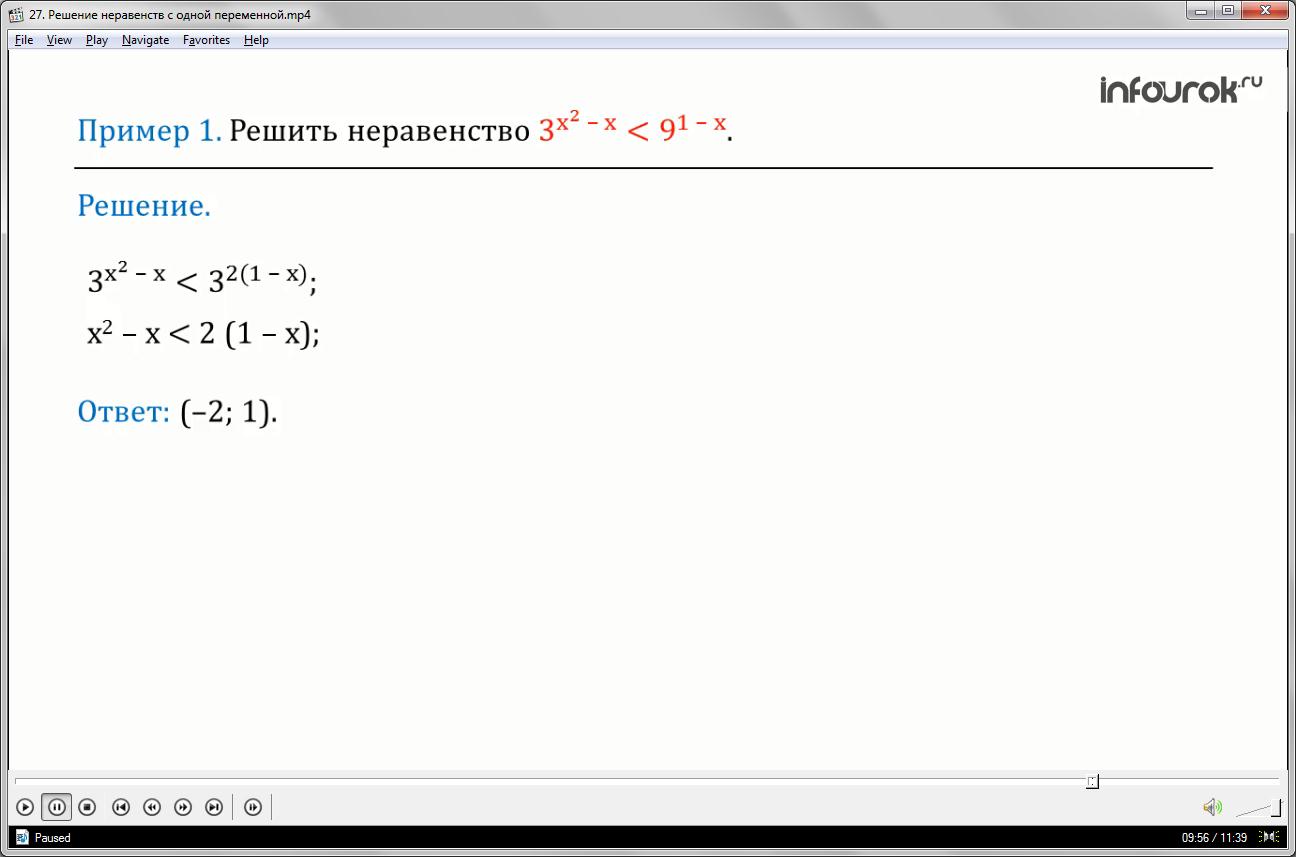
Решить неравенство три в степени икс квадрат минус икс меньше девяти в степени один минус икс.
Решение
Девять представим как три в квадрате, тогда перепишем неравенство в виде три в степени икс квадрат минус икс меньше трех в степени два умноженное на один минус икс.
Применяя теорему три (один), получим неравенство равносильное исходному неравенству, решением которого является интервал от минус двух до единицы. Следовательно, этот интервал есть множество всех решений исходного неравенства.
Ответ: интервал от минус двух до единицы.
Задание 4
Решить неравенство четыре в степени пять минус два икс меньше нуля целых двадцати пяти сотых.
Решение
Представим правую часть в виде четырех в степени минус один, получим показательное неравенство с основанием четыре.
Так как основание степени равно четырем больше одного, то по теореме шесть (один) имеем равносильное неравенство: пять минус два икс меньше минус единицы;
Выполнив равносильные преобразования, получим неравенство икс больше трех.
Наносим на координатную прямую множество решений и получаем ответ: открытый луч от трех до плюс бесконечности.
Задание 5
Решить неравенство логарифм выражения один плюс два икс по основанию ноль целых пять десятых больше минус единицы. Заменим минус один на логарифм двух по основанию ноль целых пять десятыхи, выполнив потенцирование, получим равносильное неравенство —
один плюс два икс меньше двух. Учитывая условие теоремы, получим еще одно неравенство один плюс два икс больше нуля.
Получаем и решаем систему неравенств. Решением которой, а значит, и данного неравенства является интервал от минус нуля целых пяти десятых до нуля целых пяти десятых.
Ответ: от минус нуля целых пяти десятых до нуля целых пяти десятых.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8143 |
| Номер материала | 1076 |