
Урок "Решение рациональных уравнений методом введения новой переменной"

Краткое описание документа:
Уравнение вида ax4 + bx2 + c = 0 называется биквадратным уравнением. Абсолютно любое уравнение такого типа можно решить при помощи ввода новой переменной и последующего решения уравнения относительно нее. После проводят обратную замену и находят искомый x.
Давайте рассмотрим, как применять этот метод при решении рациональных уравнений.

Дано уравнение: x4 – 4x2 + 4 = 0.
Решение
Для решения данного уравнения необходимо ввести новую переменную, которая имеет вид y =x2. Также справедливо следующее равенство: x4 = (x2)2 = y2. Исходное уравнение переписываем следующим образом: y2 – 4y + 4 =0. Это обычное квадратное уравнение, решив которое, вы получите корни y1 = y2 = 2. Поскольку y = x2, то решение этого задания сводится к решению еще одного уравнения, а именно: x2 = 2. Находим ответ: +-√2.
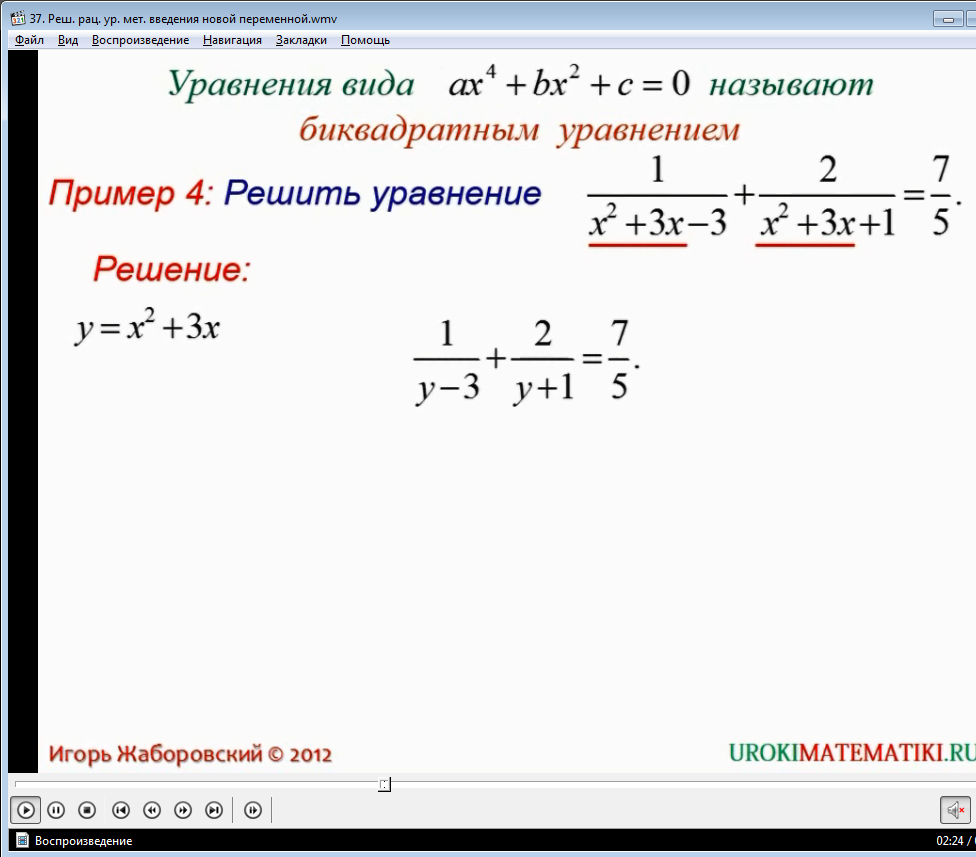
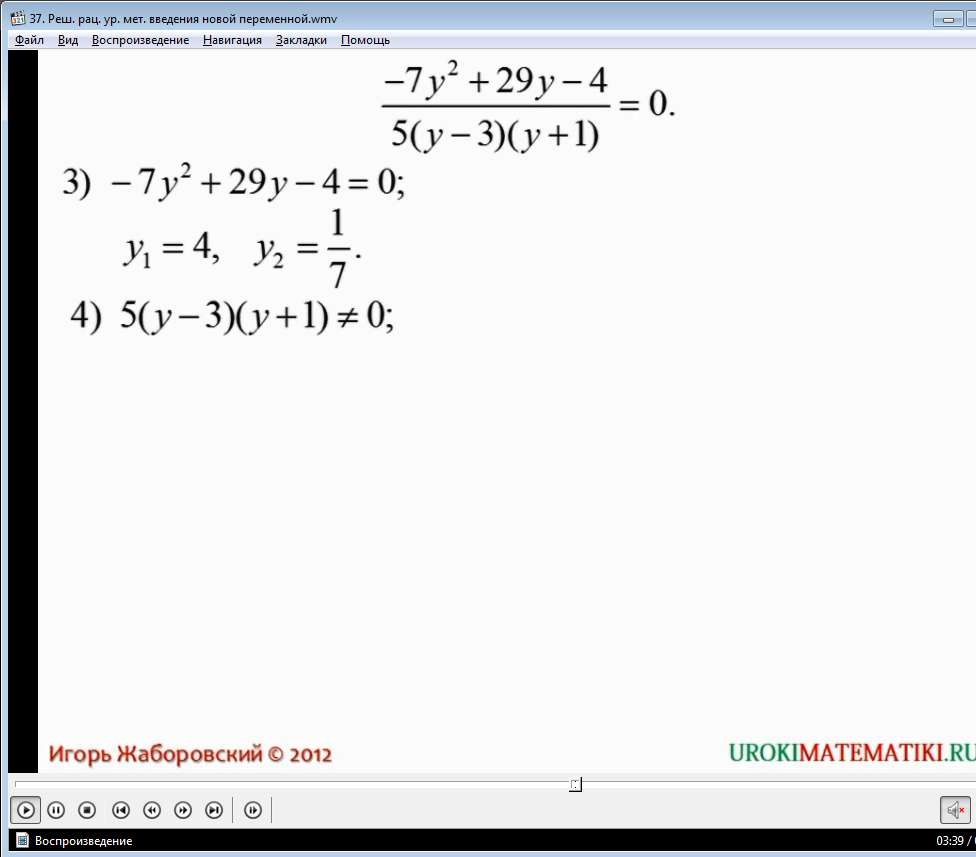
В данной ситуации, метод введения переменной был «адекватен ситуации», то есть было явно видно, какое выражение заменить новой переменной, но так бывает не всегда. В основном, выражение, которое можно заменить, проявляется только в процессе преобразования и упрощения исходного выражения. Разбор подобного примера вы можете посмотреть в видеоуроке.
Свойства функции y = k/x, при k >0
В видеоуроке вы познакомитесь с основными свойствами гиперболы, опираясь на её геометрическую модель.
1. D(f) = (-∞;0) ∪ (0; ∞) – область определения функции состоит из всех чисел, кроме 0.
2. При x > 0 => y > 0, а при x < 0 => y < 0.

3. При k > 0 функция убывает на открытом луче (-∞;0) и на открытом луче (0; ∞).
4. Функция y = k/x не имеет ограничений сверху и снизу.
5. Функция y = k/x не имеет наибольших и наименьших значений.
6. Непрерывна на промежутке(-∞;0) и (0; ∞), претерпевая разрыв при х = 0.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 4419 |
| Номер материала | 527 |