
Урок "Решение треугольников"

Краткое описание документа:
Видеоурок «Решение треугольников» демонстрирует, как в решении геометрических задач применяются полученные теоретические знания. В дальнейшем при изучении математики не раз будут возникать основные и промежуточные задачи, требующие умения применять знания из этого раздела. В видеоуроке рассматривается три вида задач по решению треугольников, а также продемонстрирован пример решения практической задачи с использованием знаний данной раздела математики. Задача видеоурока –формировать умение решать задачи по данной теме, закреплять имеющиеся знания. Ученикам может быть продемонстрирован данный материал перед тем, как начать решать задачи. Он может заменить объяснение учителя, а также может послужить наглядным пособием, сопровождающим объяснение учителя.
В видеоуроке используются анимационные эффекты, выделение цветом, голосовое сопровождение. Такое сочетание инструментов создает комплексное влияние на удержание внимания, на процессы запоминания.
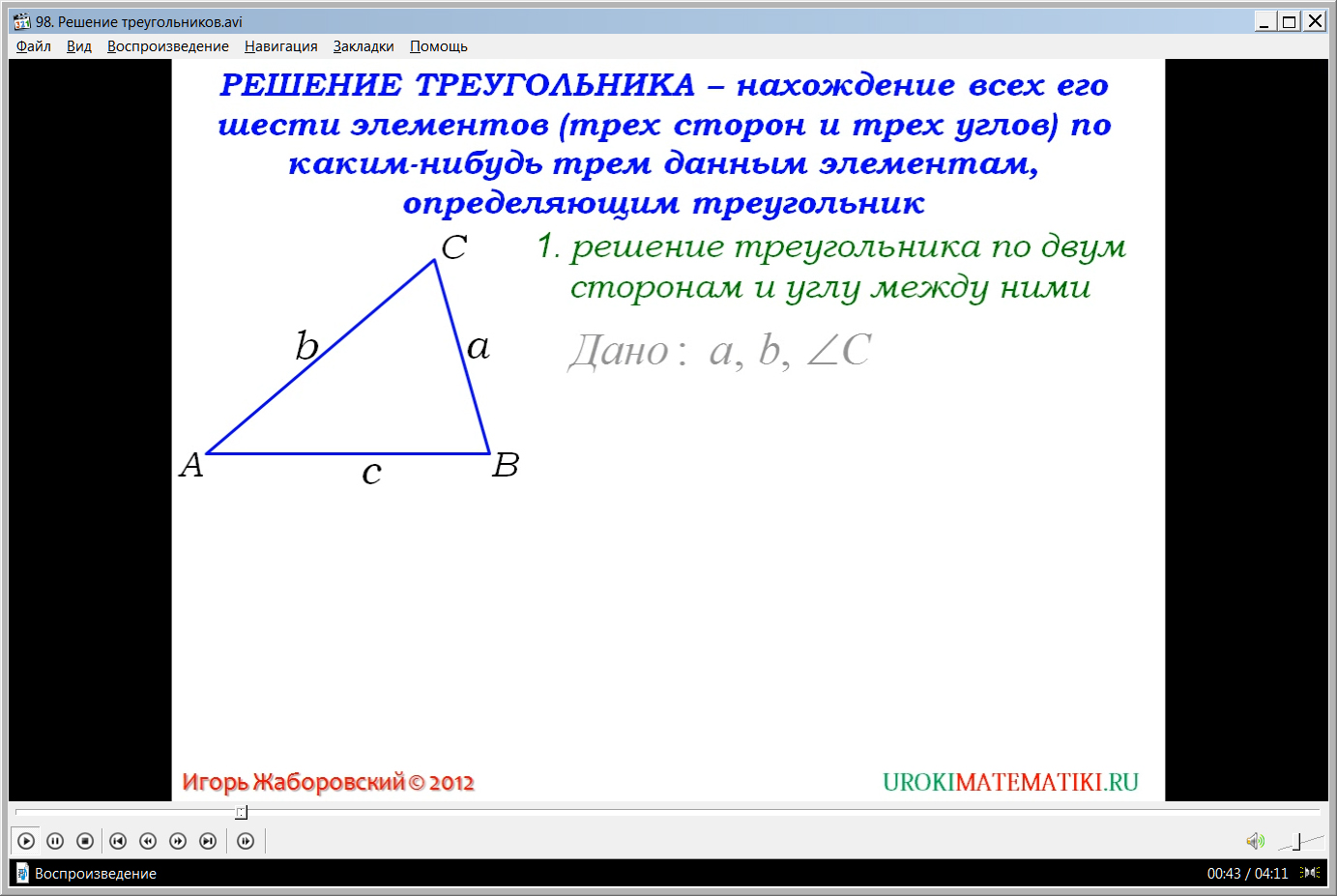
Видеоурок начинается с названия темы. Далее разъясняется смысл понятия «решение треугольника». Отмечается, что данное понятие связано с нахождением всех его шести элементов – сторон и углов по заданным некоторым элементам. Предлагается рассмотреть решение типовых задач на решение треугольника. Для этого на экране строится треугольник АВС, стороны которого обозначены АВ=с, ВС=а, СА=b. На примере этого треугольника демонстрируется решение типовых задач.
Задача первого типа – на решение треугольника по двум его сторонам и углу, образованному ими. На рисунке отмечаются и выделяются цветом заданные элементы a, b, угол C. Необходимо найти недостающие углы А и В, а также оставшуюся неизвестной сторону с. Решение данной задачи требует применения теоремы косинусов, освоенной на предыдущих уроках. Значение длины стороны с определяется по формуле с=√(а2+b2-2аbcosC). Также используя теорему косинусов определяется косинус угла А по формуле cosA=(b2+c2-a2)/2bc. Величину оставшегося угла можно найти, используя теорему о сумме углов треугольника ∠В=180°-∠А-∠С.
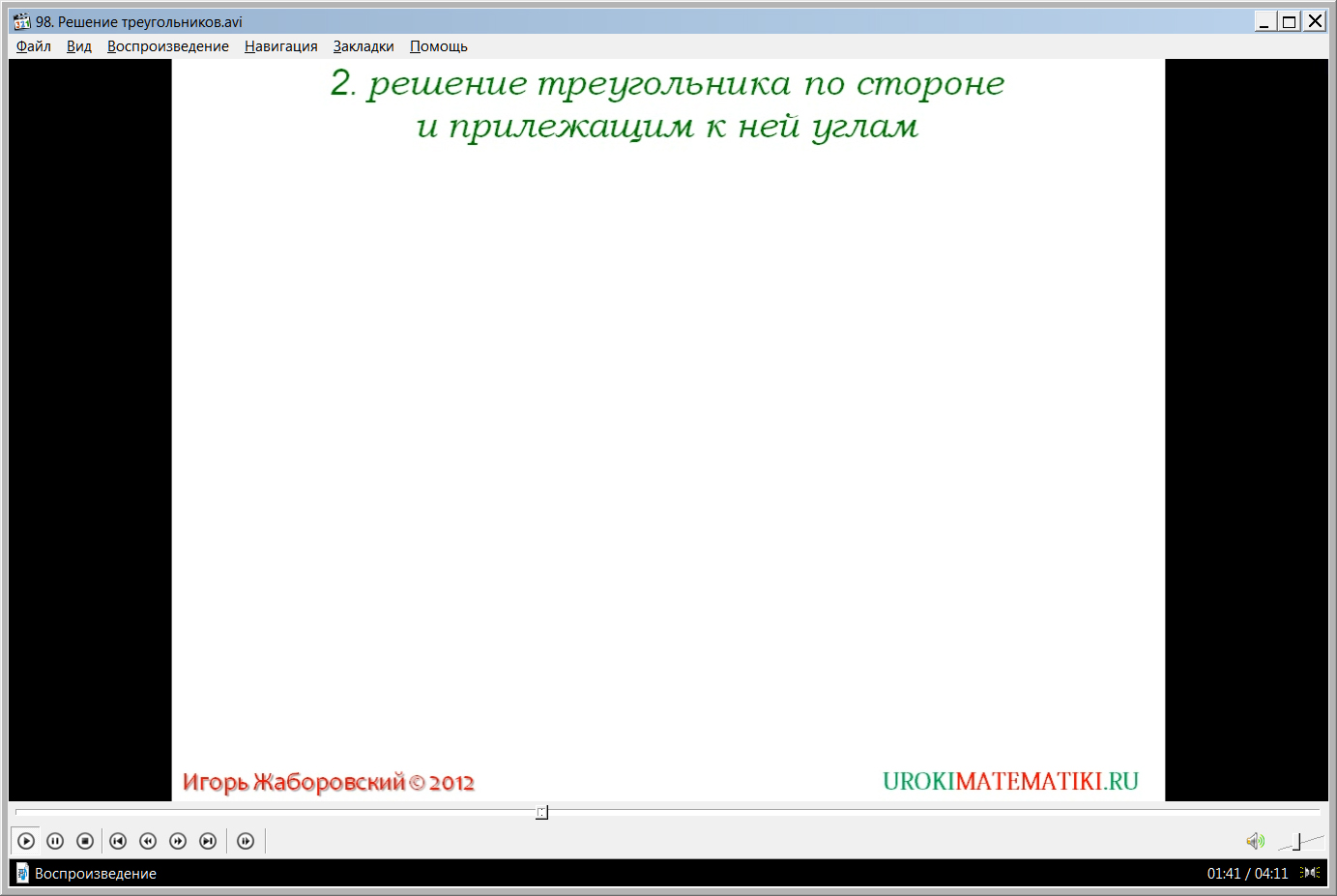
Вторая задача состоит в поиске неизвестного угла и двух сторон по известным двум углам и стороне, к которой они прилежат. На экране демонстрируется треугольник АВС, в котором выделены известная сторона а, а также углы ∠С и ∠В. Неизвестный угол легко находится по теореме суммы углов в треугольнике ∠А=180⁰-∠В-∠С. Для нахождение длин сторон можно использовать известную школьникам теорему синусов. Применяя ее, получаем b=а·sinВ/ sinА и с= а·sinС/ sinА
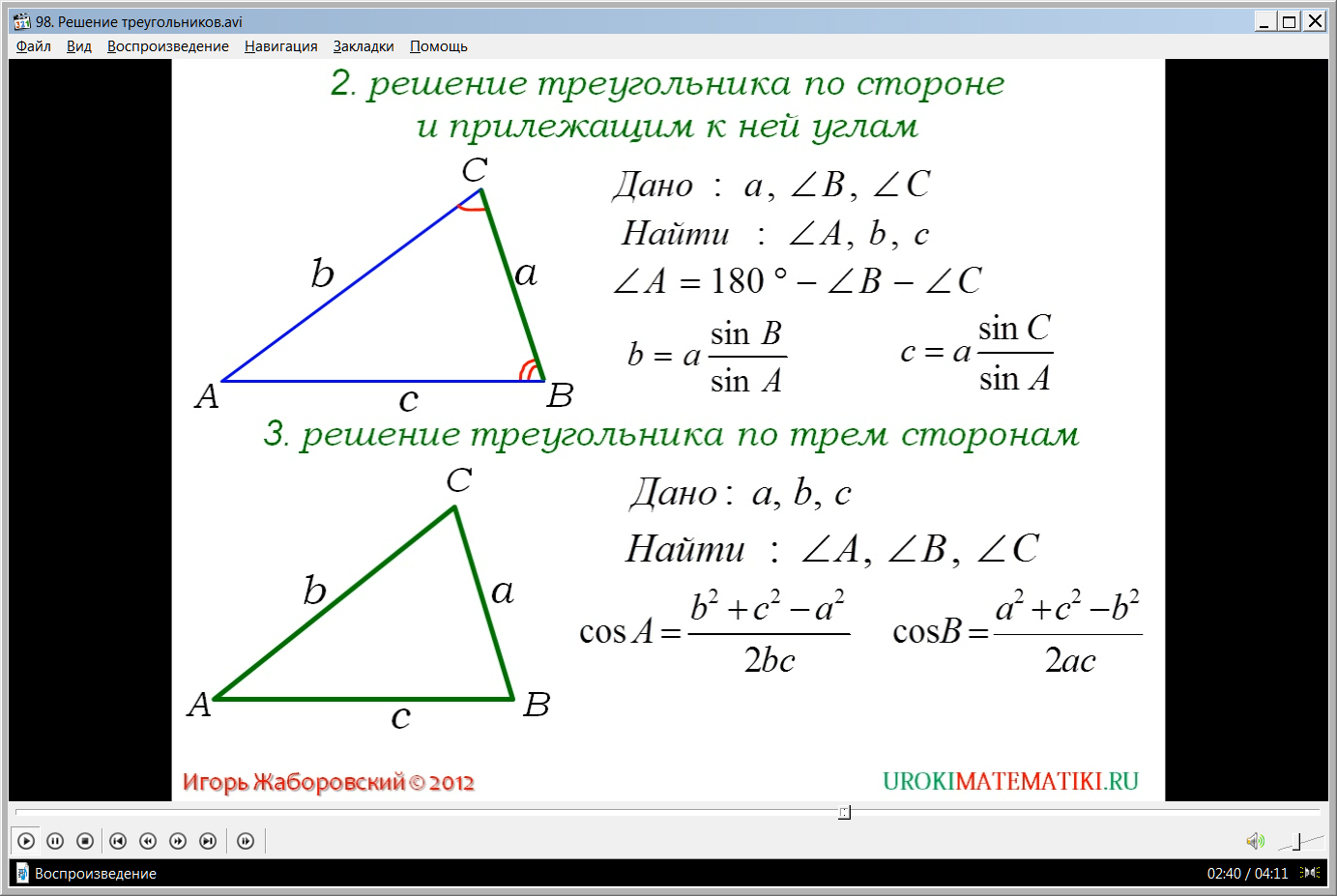
В задаче третьего вида требуется найти углы треугольника, в котором известны три его стороны. На экране построен треугольник АВС. В нем отмечены стороны а, b, c. Для вычисления величины предлагается применить теорему косинусов. Из нее следует, что cosA=(b2+c2-a2)/2bc, cosВ=( a2+c2- b2)/2аc. Для нахождения угла С можно применить теорему о сумме углов треугольника ∠С=180⁰-∠А-∠В.
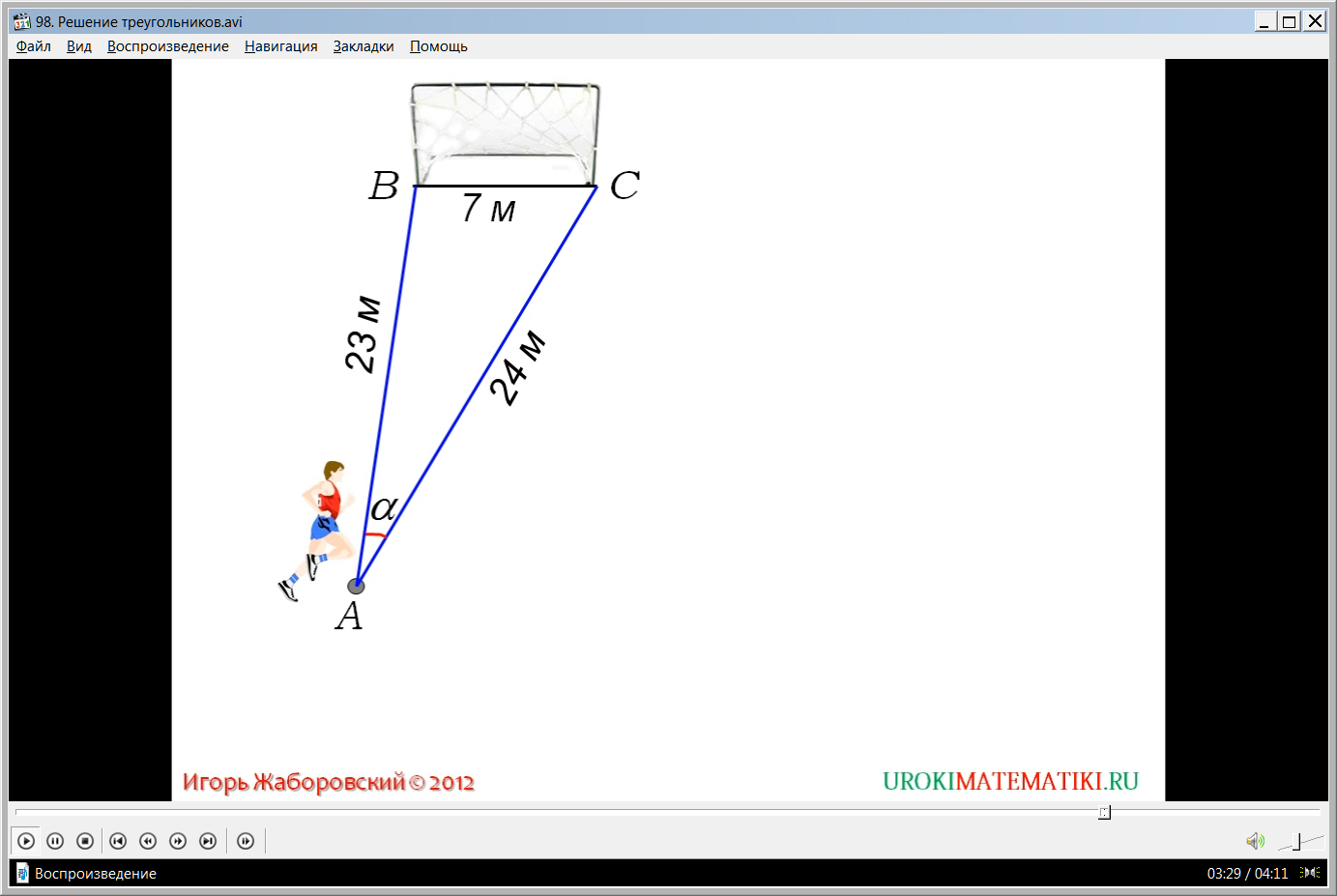
В качестве примера для закрепления материала рассматривается решение задачи, в которой футболист бьет мячом по воротам, от одного основания которых до места удара 23 м, а от второго основания – 24 м. Линия ворот вместе линиями, проведенными от игрока до снований ворот, составляет треугольник с игроком в вершине А и основаниями ворот в вершинах В и С. Известно, что ширина ворот 7 м. Необходимо найти величину угла α, который составляет угол попадания мяча в ворота. Уточняется, что сторонами данного треугольника будут с=АВ=23 м, b=АС=24 м, а=ВС=7 м. Очевидно, для решения данного треугольника следует применить теорему косинусов cosA=(b2+c2-a2)/2bc=(242+232-72)/2·24·23. По таблице косинусов находится значение угла α≈16⁰57‘.
Видеоурок «Решение треугольников» поможет поднять эффективность традиционного урока в школе. Также данный материал может помочь ученику самостоятельно освоить материал, углубить его понимание. Наглядное пособие пригодится и в ходе дистанционного обучения.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 8107 |
| Номер материала | 762 |