
Урок "Вынесение общего множителя за скобки"

Краткое описание документа:
В ходе различных математических операций при работе с уравнениями и равенствами часто появляется возможность значительно упростить все действия путем вынесения некоего общего множителя за пределы самого выражения. Это позволяет не только сократить большие группы многочлена, но и упростить сам процесс решения.
Вынесение множителя позволяет также избавиться от лишних действий и оптимизировать процесс вычислений. В данном видеоуроке мы подробно изучим возможности процедуры вынесения. Например, рассмотрим выражение следующего вида:
ах + сх
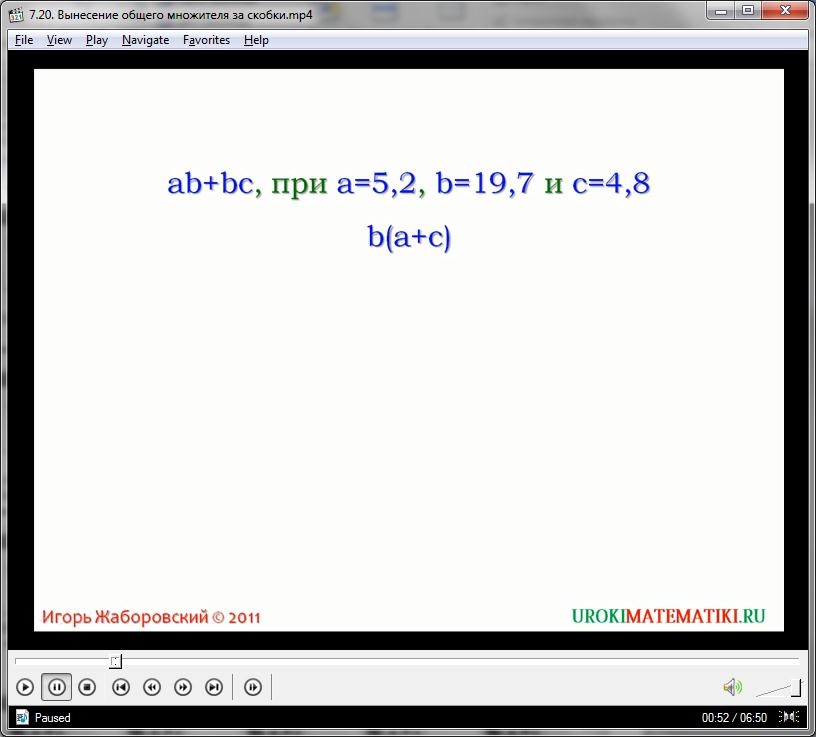
Нам необходимо его преобразовать так, чтобы при известных значениях всех переменных было легко вычислить значение всего полинома. Положим, а=1, с=2, х=5. Обратим внимание, что у обоих членов многочлена есть общая часть – множитель-переменная х. Она легко выносится за скобки, согласно распределительному закону умножения:
ах + сх = х(а + с)
Для нахождения правой части данного равенства необходимо поделить каждый одночлен исходного полинома на утвержденный общий множитель (в этом случае – х), частное записать алгебраической суммой в скобках, а сам множитель поставить перед ними. Руководствуясь заданными значениями переменных, получаем:
ах + сх = х(а + с) = 5(1 + 2) = 15
В видеоуроке сделан акцент, что вынесение множителя за скобки в представленном примере, сократило количество действий по расчету с трех до двух. В более сложных упражнениях эффект упрощения может быть ещё более значителен. А многие уравнения без применения метода вынесения множителя вообще очень сложно решить.
В общем, вынесение общего множителя за скобки в полиномах именуется процессом разложения многочлена на отдельные множители. При этом используется следующий алгоритм для обработки данных:
- Выделяется рабочая группа выражения (многочлен);
- Осуществляется поиск подходящего множителя, на который можно было бы поделить каждый одночлен;
- Производится деление мономов на выделенный множитель, при этом результаты записываются вместо одночленов, как алгебраическая сумма;
- Получившийся многочлен заключается в скобки, общий множитель ставится перед ними.
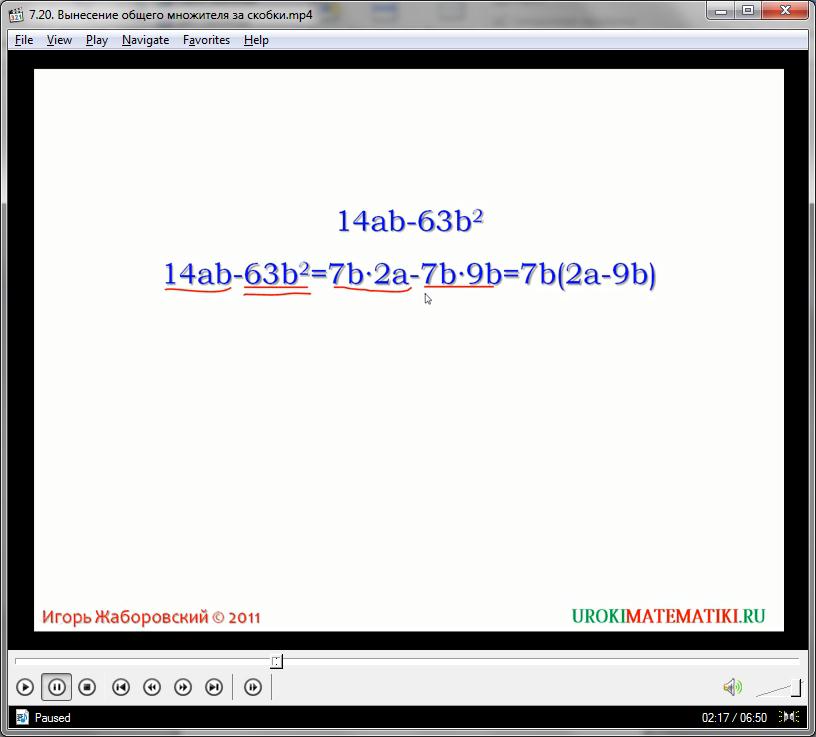
При выборе множителя часто возникают проблемы. Во-первых, он должен отвечать максимальному количеству мономов, в идеале – делить все одночлены. Во-вторых, в комплексных задачах необходимо подбирать такой множитель, чтобы он позволял провести решение всего упражнения дальше, облегчая всю процедуру. Как правило, если нет строгого условия извне (в уравнениях, к примеру), то множитель подбирается по принципам: подходящий всем мономам и являющийся наибольшим по степени и коэффициенту при переменной. Иначе говоря, множитель должен включать все переменные, наибольшую возможную степень, а также наибольший кратный числовой коэффициент. Рассмотрим пример:
2х2у – 8х2у + 4х2 +4х3у2
Вполне очевидно, что в этом выражении для всех одночленов наиболее приемлемым множителем будет переменная х, взятая во второй степени (максимально допустимой) и с числовым коэффициентом, равным 2, т.е. 2х2:
2х2у – 8х2у + 4х2 +4х3у2 = 2х2(у – 4у + 2ху2) = 2х2(2ху2 – 3у)
Производим действия в скобках, получаем итоговый ответ, представляющий собой произведение многочлена на одночлен-множитель.
Рассмотрим ещё один пример. Необходимо преобразовать выражение вида:
2х(4-у) + х(у-4)
С первого взгляда, тут трудно что-либо вынести за скобки, кроме переменной х, вынесение которой создаст двойные скобки и лишь усложнит многочлен, поэтому данный шаг нецелесообразен. Однако следуя стандартной логике и базовым правилам математического сложения, можно уверенно записать, что:
(у-4) = -(4-у)
Если минус у правого выражения внести внутрь, то все внутренние знаки сменятся на противоположные, образуя выражение, полностью идентичное левой части. Поэтому, корректно будет записать:
2х(4–у) + х(у–4) = 2х(4–у) – х(4– у)
Теперь же оба члена многочлена содержат общий множитель (4– у), который легко вынести за скобки, продолжив дальнейшие вычисления:
2х(4–у) – х(4– у) = (4– у)(2х – х) = (4– у)х = 4х – ух
Последние два этапа расчетов не относятся к общей процедуре вынесения множителя, и являются индивидуальным решением данного примера. Сам процесс вынесения дает нам произведение двух элементарных биномов.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5970 |
| Номер материала | 453 |