
Урок "Решение задач с помощью уравнений"

Краткое описание документа:
При помощи уравнений можно быстрее и легче решать различные типы задач. Но при этом надо придерживаться следующего плана:
- обозначить неизвестное в задаче число буквой и составить необходимое по условию задачи, уравнение;
- решить полученное уравнение, применив необходимые знания;
- истолковать и обобщить результат в соответствии со смыслом задачи.
Итак, попробуем на этих трёх шагах решить следующую задачу. Задача первая: в равнобедренном треугольнике одна из сторон в три раза больше другой. Какова длина сторон треугольника, если известно, что его периметр равен сто девятнадцать сантиметров?
Итак, пусть одна из сторон треугольника равна Х сантиметров, то есть неизвестное обозначаем за Х. Тогда вторая сторона равна 3Х сантиметров, потому что по условию задачи вторая сторона в три раза больше. Если первая Х, то вторая 3Х. Выразим через Х длину третьей стороны. Так как треугольник равнобедренный, то она равна либо Х, либо 3Х, потому что в равнобедренном треугольнике две стороны одинаковые. Если одна из сторон Х, а другая 3Х, то третья – равна, либо первой, либо второй; либо Х, либо 3Х. Однако третья сторона не может быть равна Х, так как в этом случае сторона треугольника оказалась бы больше суммы двух других сторон. Есть понятие того, что любая сторона треугольника не должна быть больше, чем сумма двух других сторон треугольника, поэтому третья сторона нашего треугольника будет обязательно 3Х. По условию задачи периметр треугольника равен сто девятнадцать сантиметров, значит Х + 3Х + 3Х =119. Периметр помним это сумма длин сторон треугольника. Решим составленное уравнение.
Х+3Х+3Х=7Х
7Х+119. Делим обе части на семь, получаем Х=17. Таким образом, мы нашли одну из сторон треугольника, которую обозначали за Х, её длина семнадцать сантиметров. Две оставшихся стороны равны по 3Х, то есть 3 умножить на 17, это 51 сантиметр. Записываем ответ – стороны треугольника равны 17 сантиметров, 51 сантиметр и 51 сантиметр.
Рассмотрим ещё одну задачу.
Задача два: требуется найти трёхзначное число, удовлетворяющее следующему условию: если к нему приписать справа цифру пять и из полученного четырёхзначного числа вычесть три тысячи двенадцать, то разность будет в шесть раз больше трёхзначного числа. Чему равно это число?
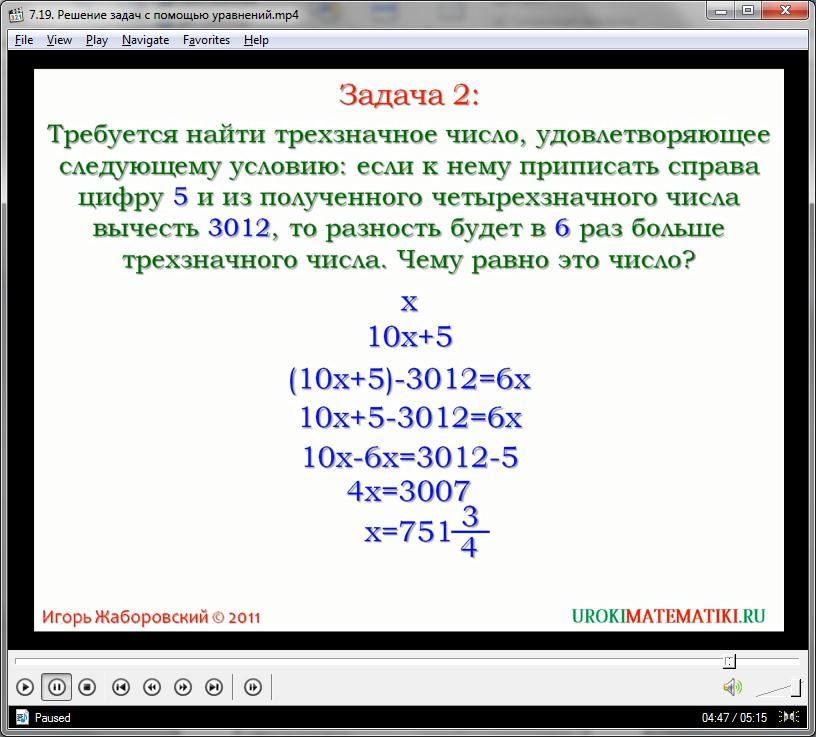
Итак, пусть Х искомое трёхзначное число, тогда приписав к нему, справа цифру пять, получим четырёхзначное число равное десять Х плюс пять. То есть Х это трёхзначное число, когда мы к трёхзначному числу приписываем какую ни будь цифру, число становится четырёхзначным, то есть оно становится большим на один десяток. Поэтому Х умножаем на десять и прибавляем пять. По условию задачи разность десять Х плюс пять минус три тысячи двенадцать в шесть раз больше числа Х. Значит, эта разность равняется 6Х. Решим составленное уравнение. Скобки опускаем, слагаемое, содержащее Х, переносим в левую часть, а не содержащее Х переносим в правую часть. Приводим подобные, делим обе части на четыре, получаем Х равно семьсот пятьдесят одна целая три четвертых. По смыслу задачи Х натуральное число, а корнем уравнения является дробное число. Значит, не существует трёхзначного числа, которое удовлетворяло бы данное условие. Поэтому запишем ответ – такого трёхзначного числа не существует.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5248 |
| Номер материала | 452 |