
Урок "Решение уравнений, сводящихся к линейным"

Краткое описание документа:
Решая уравнения, мы для того, чтобы упростить его, выполняем тождественные преобразования выражений. В уравнениях с одной переменной иногда решение уравнения можно свести к решению равносильного ему линейного уравнения с одной переменной.
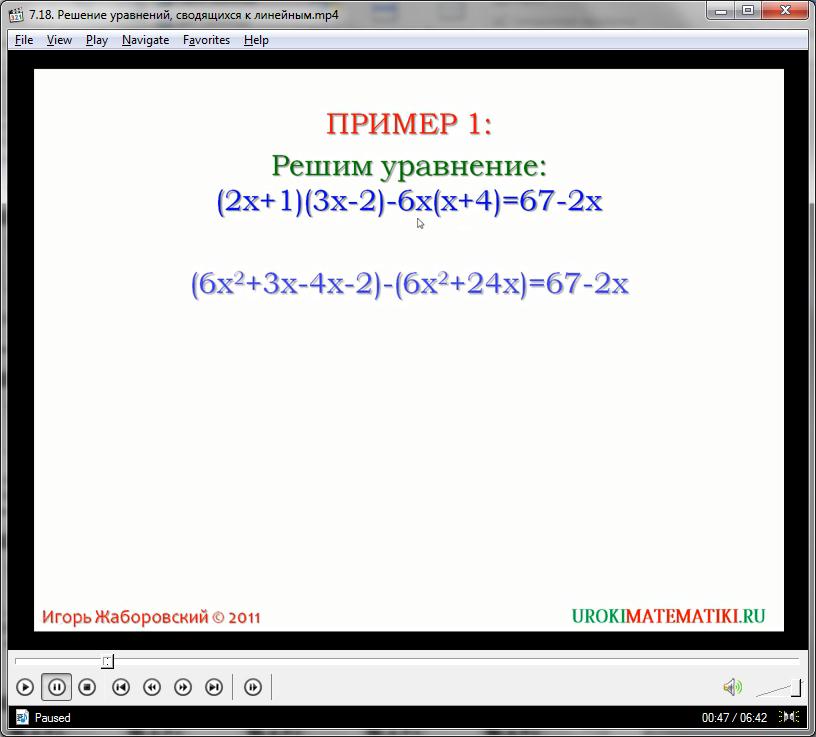
Рассмотрим на примерах. Решим уравнение (2x+1)(3x-2)-6x(x+4)=67-2x. В левой части уравнения умножим многочлен 2x+1 на многочлен 3x-2, а также одночлен 6x на многочлен x+4. После умножения многочлена 2х+1 на многочлен 3х-2 получим многочлен 6х2+3х-4х-2, а после умножения одночлена 6х на многочлен х+4 получим многочлен 6х2+24х. Наше уравнение примет вид (6х2+3х-4х-2)-(6х2+24х)=67-2х. После этого раскроем скобки и получим 6х2+3х-4х-2-6х2-24х=67-2х. Перенесем слагаемые с неизвестным в левую часть, а без неизвестного – в правую. Новое равносильное уравнение выглядит так 6х2-6х2+3х-4х+2х-24х=67+2. Приведем подобные. Получаем -23х=69. Разделим обе части уравнения на -23. Получаем х=-3. Мы последовательно заменяли уравнения равносильными. Значит исходное уравнение равносильно уравнению -23х=69 и имеет единственный корень – число -3.
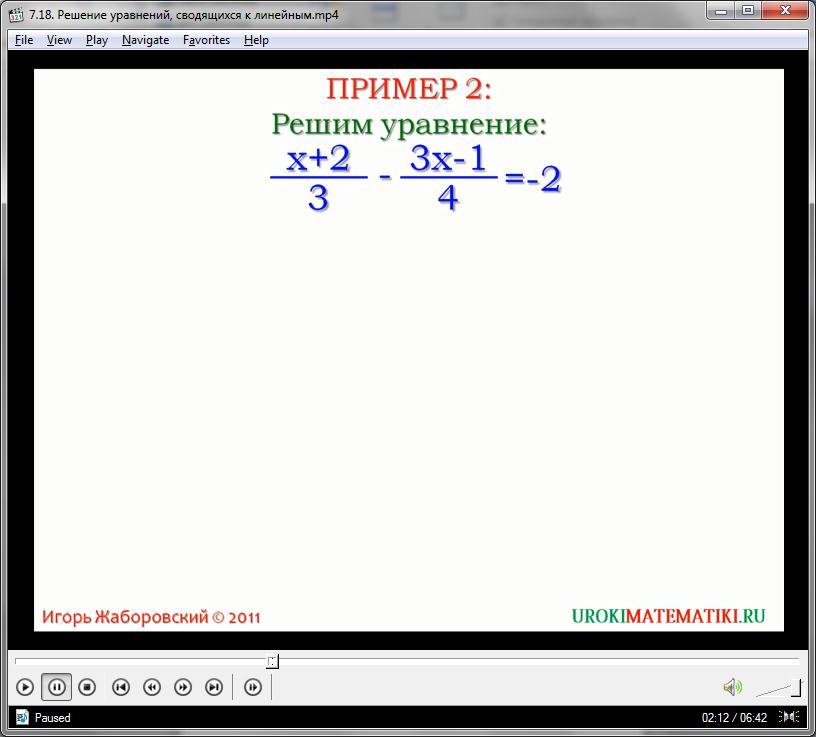
Пример второй. Решим уравнение (х+2)/3-(3х-1)/4=-2. В левой части этого уравнения находятся дроби (х+2)/3 и (3х-1)/4. Умножим обе части уравнения на наименьший общий знаменатель этих дробей – число 12. [(x+2)/3-(3x-1)4]•12=-2•12. Раскроем скобки и умножим каждую дробь на 12. Получим (х+2)12/3-(3х-1)12/4+-24. В первой дроби сократится 12 и 3, а во второй 12 и 4. После сокращения наше уравнение станет 4(х+2)-3(3х-1)=-24. Таким образом, мы освободились от знаменателей. После раскрытия скобок, получим 4х+8-9х+3=-24. Все, что содержит переменную, переносим в левую часть, а все, что не содержит переменную – в правую. Уравнение принимает вид 4х-9х=-24-8-3. Приведем подобные и получим –5х=-35. Делим обе части уравнения на -5 и выходит, что х=7. Заменяя шаг за шагом уравнение равносильным параметром, мы получили линейное уравнение -5х=-35, равносильное данному. Данное линейное уравнение имеет единственный корень – число 7.
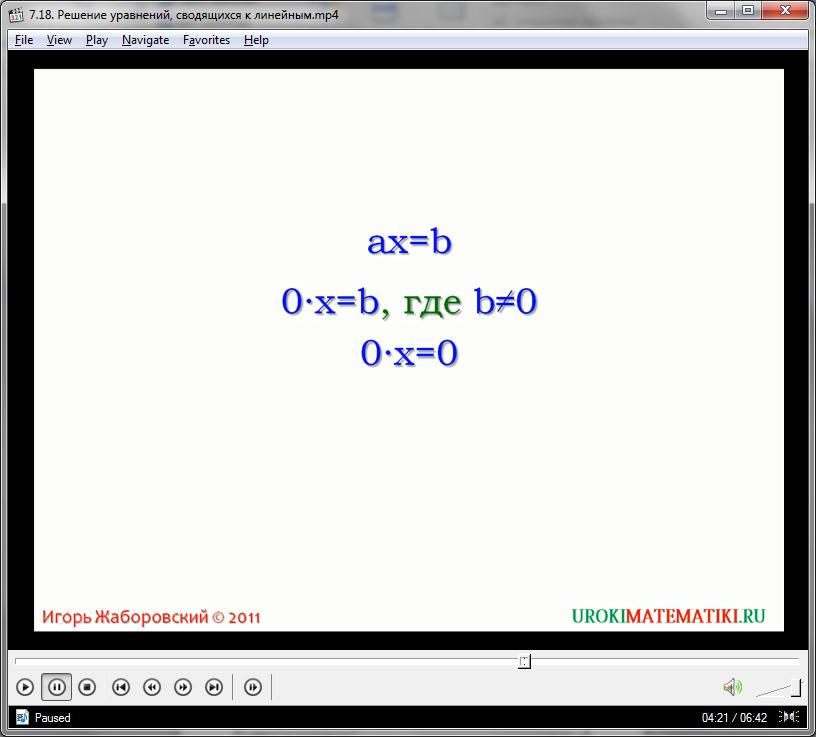
В рассмотренных примерах решение исходного уравнения сводилось к решению линейного уравнения вида ax=b, в котором коэффициент а не равен 0.
Однако может случиться и так, что заменив одно уравнение на другое, равносильное ему, мы можем получить линейное уравнение вида 0х=b, где b не равно 0 либо 0х=0. В первом случае можем сделать вывод, что исходное уравнение не имеет корней, потому что в левой части уравнения 0, а в правой число не равное 0. Во втором случае уравнение имеет бесконечное число корней, потому что в левой части уравнения всегда будет 0, а в правой тоже 0. Равенство будет выполняться всегда, вне зависимости от значения переменной.
Пример третий. Решим уравнение (2х-7)/2-(4х-1)/4=0. Снова наше уравнение содержит дроби, поэтому умножаем обе части уравнения на наименьший общий знаменатель. Это число 4. Получим [(2x-7)/2-(4x-1)/4]•4=0•4. Раскроем скобки: 4(2х-7)/2-4(4х-1)/4=0. Сократим множители и получим уравнение 2(2х-7)-(4х-1)=0. Снова раскроем скобки: 4х-14-4х+1=0. Перенесем слагаемые с неизвестным в левую часть уравнения, а без неизвестного – в правую. Уравнение примет вид 4х-4х=14-1. Приводим подобные и получаем 0х=13. Это уравнение не имеет корней, потому что 0х равно 0 при любых значениях х. Выходит, что равенство не будет достигнуто никогда, ни при каких значениях х. Значит и равносильное ему исходное уравнение не имеет корней.
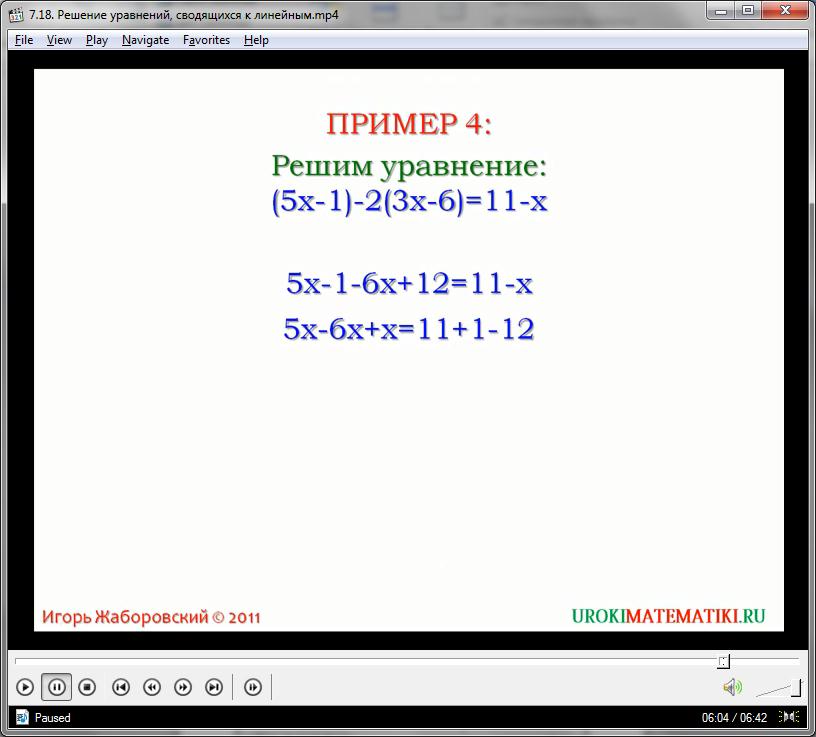
Пример четвертый. Решим уравнение (5х-1)-2(3х-6)=11-х. Раскроем скобки: 5х-1-6х+12=11-х. Перенесем слагаемые, содержащие х, в левую часть, а не содержащие х – в правую часть уравнения. Получим 5х-6х+х=11+1-12. Приведем подобные: 0х=0. Вот это уравнение 0х=0, а значит и равносильное исходное уравнение, имеет бесконечное множество корней. Так как 0, умноженный на любое число, равняется 0 то равенство выполняется при любом значении х.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8640 |
| Номер материала | 451 |