
Урок "Сфера и шар"

Краткое описание документа:
Видеоурок «Сфера и шар» предназначен для обеспечения наглядности при подаче учебного материала по данной теме на уроке геометрии. В ходе демонстрации представляются понятия сферы и шара с точки зрения стереометрии, даются сравнительные характеристики данных понятий, выводится формула для вычисления объема шара. Задача видеоурока – наглядно представить учебный материал, способствовать усвоению представляемых понятий и запоминанию определений и формул. Видеоурок может использоваться для повышения эффективности традиционного урока в качестве наглядного пособия, сопровождающего объяснение учителя или вместо объяснения учителя по новой теме.
Видеоурок активизирует процессы мышления и запоминания учеников с помощью комплекса приемов, способствующих улучшению запоминания материала и его понимания. Анимационные эффекты, используемые при построении чертежей для иллюстрации преобразований и структуры, не только удерживают внимание ученикам на изучаемом предмете, но и акцентируют внимание на важных деталях построения, углубляя понимание предмета изучения. При помощи выделения цветом и озвучивания текста определений и формул активизируется процесс запоминания изучаемого материала.
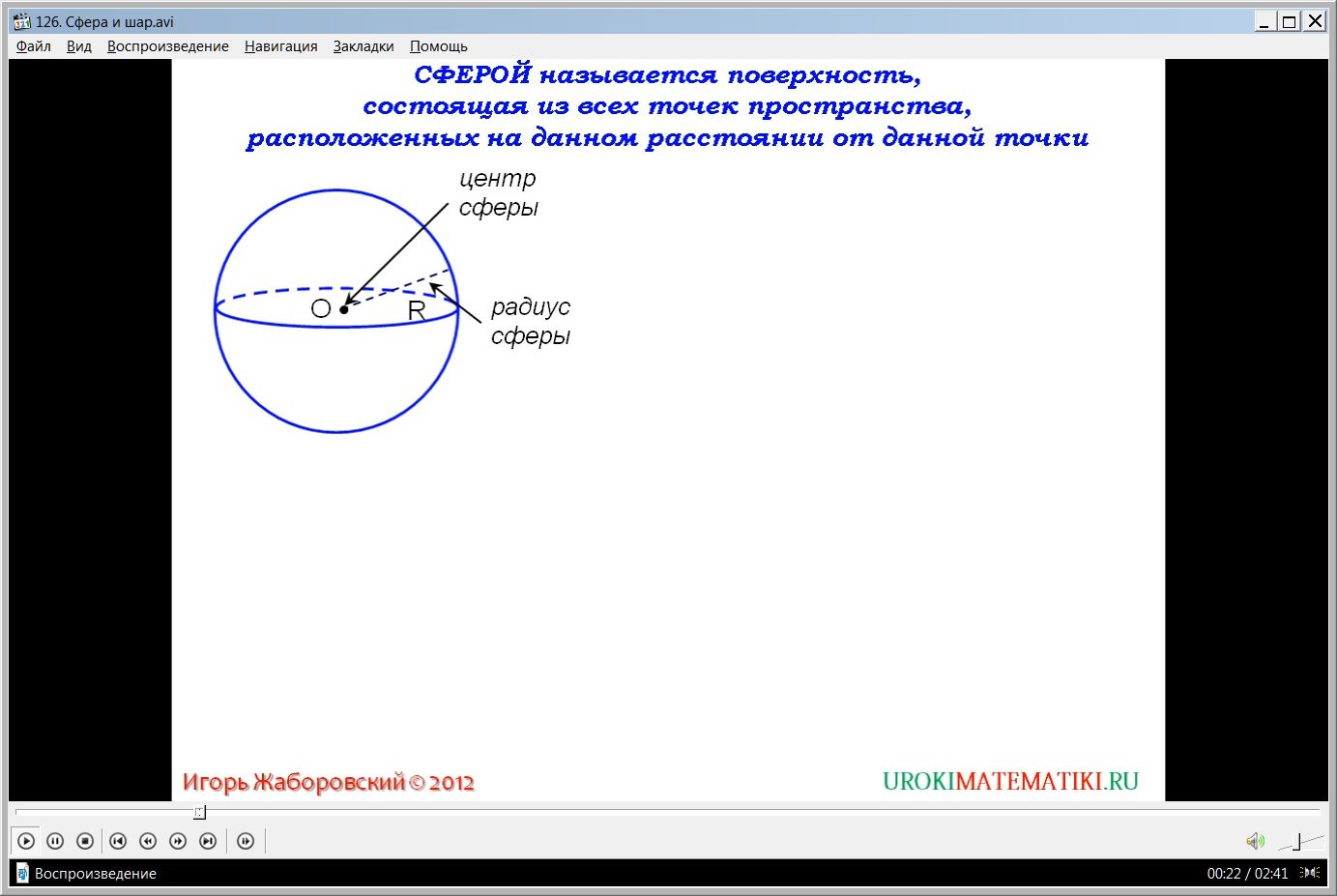
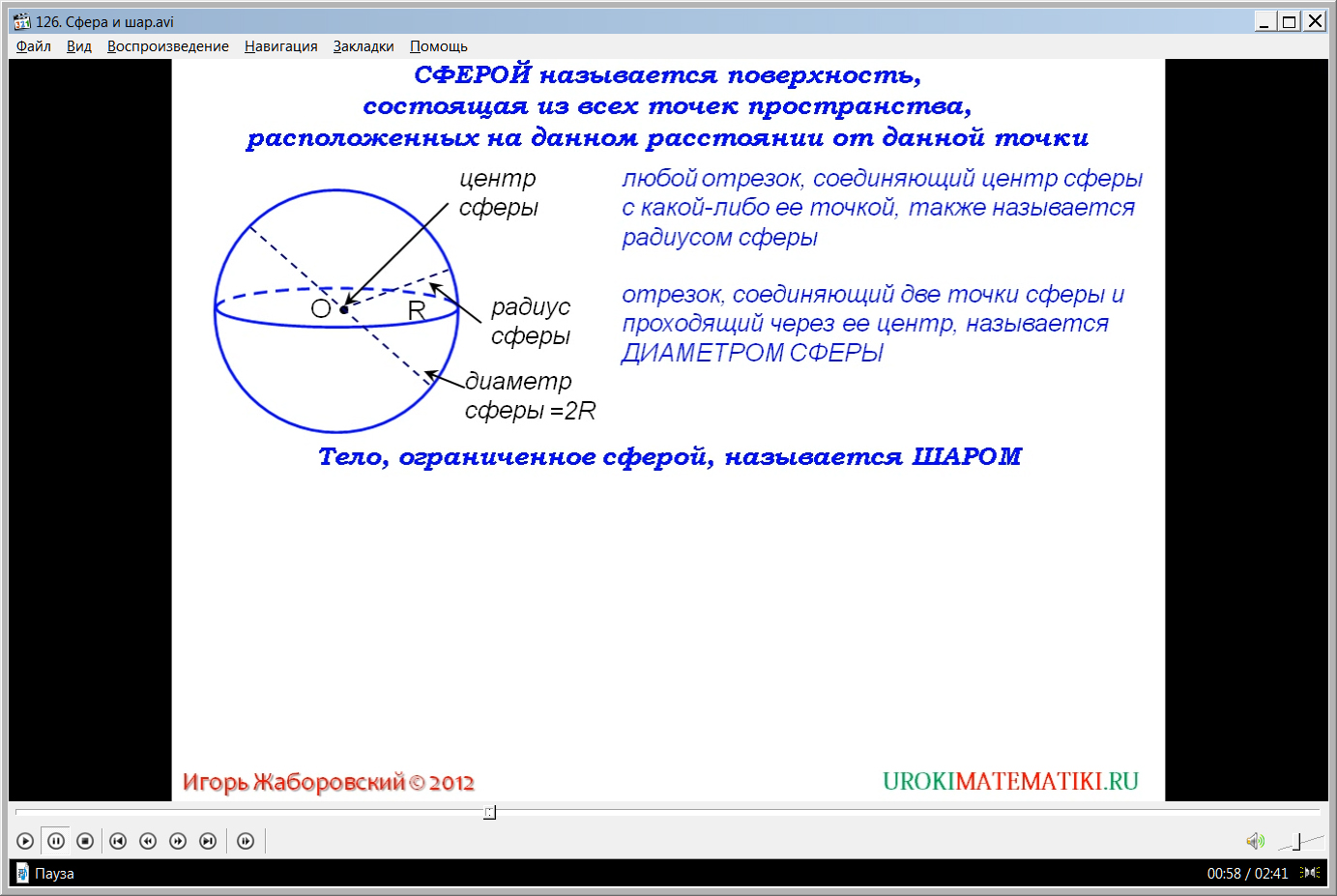
Видеоурок начинается с представления названия темы. Дается определение сферы как поверхности, состоящей из точек, равноудаленных от некоторой точки. Точку, от которой равноудалены точки сферы, называют центром сферы. На рисунке изображена сфера, отмечен ее центр, а также расстояние от центра до точек сферы, которое иначе называется радиусом сферы. Названия элементов отмечены на экране и выделены с помощью указателей. Также дано текстовое описание радиуса сферы как отрезка, соединяющего центр сферы с любой ее точкой и определение диаметра сферы как отрезка, соединяющего две ее точки и проходящий через центр. На экране строится диаметр сферы и название элемента выделяется с помощью указателя. Также отмечено, что диаметр сферы равен удвоенному ее радиусу.
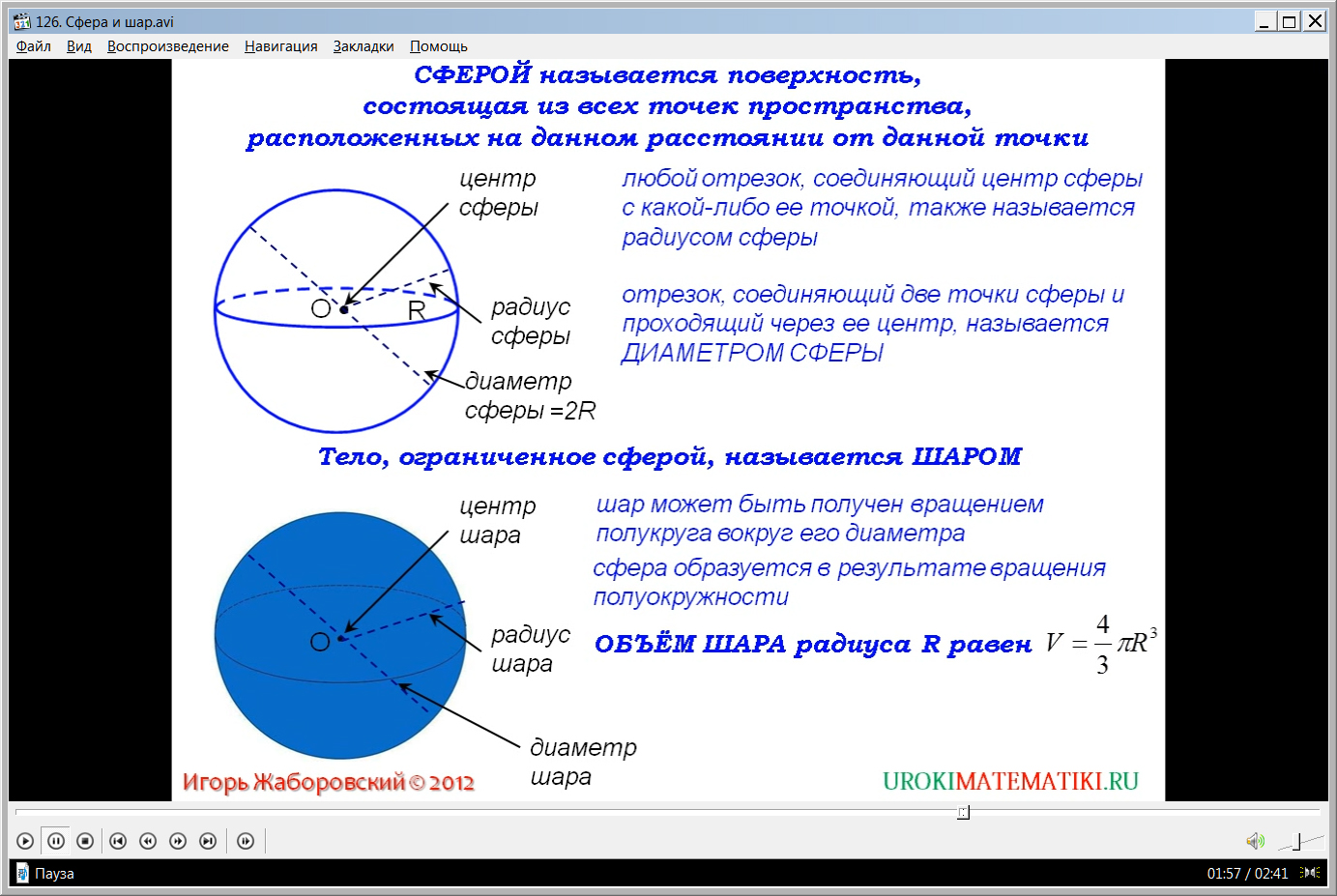
Ниже на рисунке изображается шар. Он представлен как тело, ограниченное сферой и имеющее все элементы, присущие сфере. Так, на данном шаре отмечены центр, радиус и диаметр. Замечено отличие шара от сферы – то, что он содержит не только точки, равноудаленные от центра, но и все точки, лежащие внутри сферы, то есть расстояние к которым не превышает радиуса. При этом также отмечается, что шар образуется вращением полукруга вокруг диаметра в отличие от сферы, которая образуется вращением полуокружности. Ученикам представлена формула для нахождения объема шара V=4/3(πR3). Отмечается, что для ее вывода используется принцип Кавальери
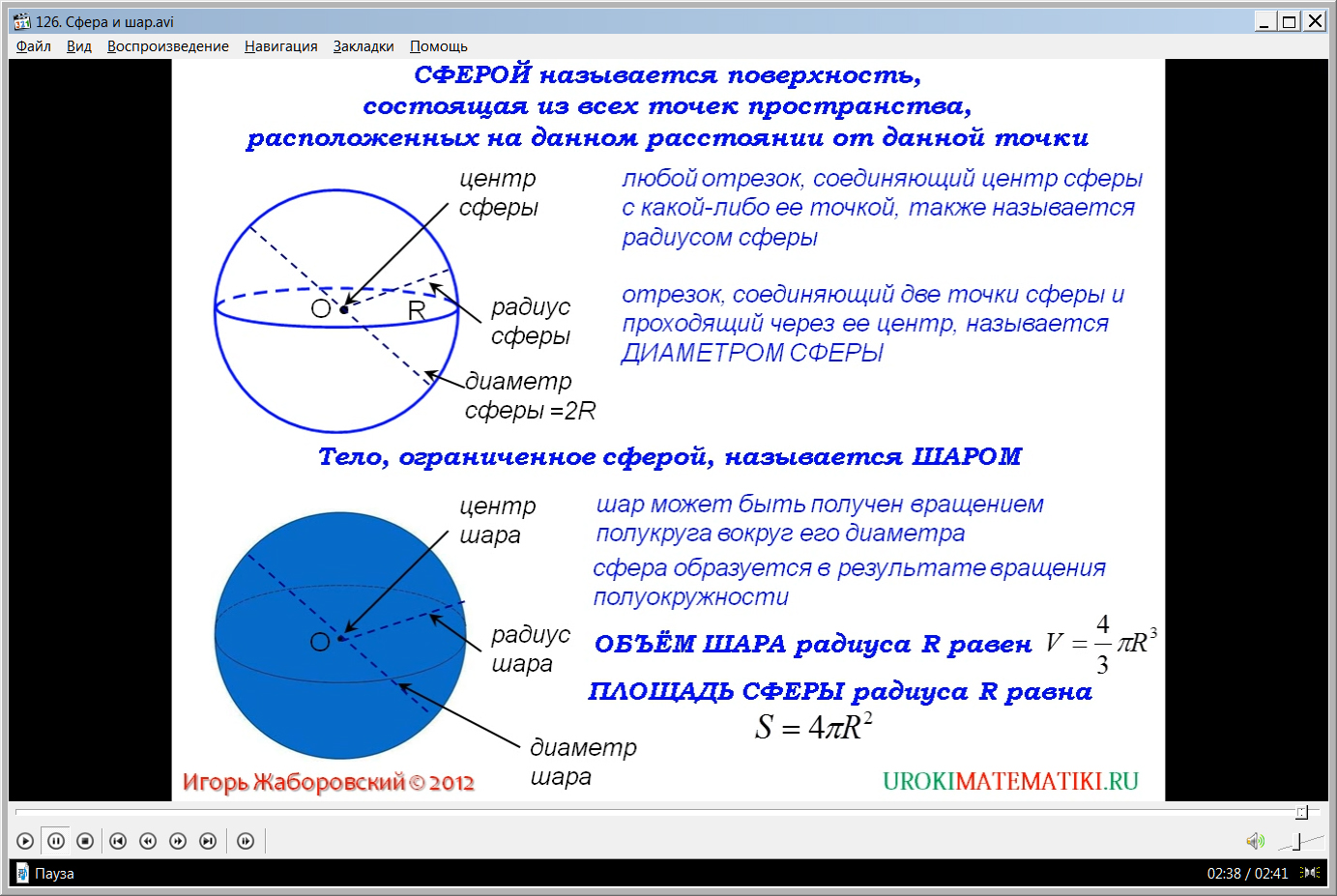
Сообщается, что для определения площади поверхности шара не может использоваться способ развертки, так как развернуть шар в плоскую фигуру сложно. Поэтому для вычисления площади поверхности шара необходимы знания, которые будут получены в курсе геометрии 11 класса. Тогда и будут предоставлены знания о том, как вычисляется площадь боковой поверхности шара. При изучении сферы в 9 классе для нахождения площади боковой поверхности дается только формула без обоснования S=4πR2.
Видеоурок «Сфера и шар» рекомендуется использовать на традиционном уроке геометрии в школе для обеспечения наглядности объяснения учителя и повышения эффективности обучения. Данный материал с успехом может быть использован при проведении дистанционного обучения. Видео также может помочь ученикам самостоятельно разобраться в особенностях предмета по данной теме.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 4863 |
| Номер материала | 734 |