
Урок "Синус и косинус суммы аргументов"

Краткое описание документа:
Видеозапись «Синус и косинус суммы аргументов» длится чуть больше 9 минут. Она имеет приятный интерфейс, который не будет раздражать восприятие школьников. Ее можно демонстрировать при проведении урока в школе. Учитель, прежде чем перейти к подробному комментированию, может включить видеозапись для просмотра учениками. Местами можно приостановить и более подробно объяснить. Это улучшит восприятие.
В курсе изучения тригонометрии школьники уже сталкивались с функциями, их основными свойствами, характером поведения. Среди них основными функциями являлись периодичные функции синуса, косинуса, тангенса и котангенса. Они имеют разные периоды и характеристики.
Школьники учились строить их графики и проводить анализ данных функций. Изучали области определения, области значений, промежутки возрастания и убывания и т. п.
В данном видеоуроке будут изучаться тригонометрические формулы, с помощью которых можно преобразовывать различные тригонометрические выражения.
Одними из основных фундаментальных формул являются синус суммы и косинус суммы, которые часто используются при решении тех или иных задач. При выполнении домашней работы, либо различных самостоятельных или контрольных работ школьники, несомненно, столкнуться с необходимостью использовать данные формулы. Поэтому является важным как следует понять данный урок, чтобы лучше и дольше запомнить.
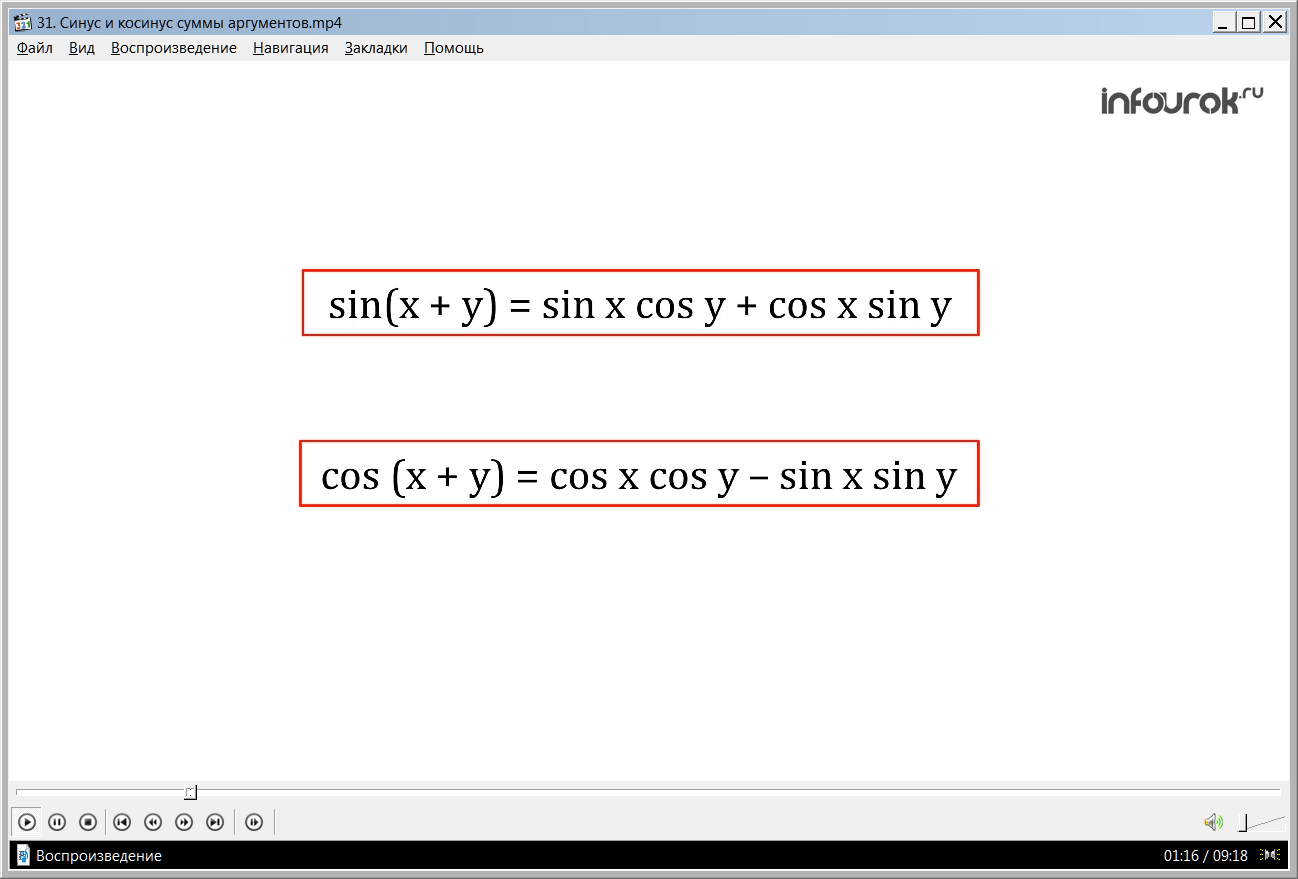
В первой части презентации будут продемонстрированы эти формулы, обведенные в красные рамки, подчеркивая тем самым важность запоминания. Мы видим, что они несколько отличаются друг от друга. Запомнить формулы не составит никакого труда, если правильно применить их на практике.
Диктор объясняет школьникам, каким образом необходимо правильно прочитать данные формулы. Некоторые учителя требуют от учеников воспроизведение в словесной форме этих формул с целью развития математической речи. Поэтому стоит внимательно прослушать речь диктора и записать при необходимости в тетради.
Далее приводится первый практический пример. Требуется найти синус 105 градуса. Диктор предлагает для решения данного примера привести уголь 105 градусов в виде суммы двух углов, а именно 45 и 60, синусы и косинусы которых школьники знают и могут вспомнить, обратившись к таблице значений тригонометрических функций.
Эти таблицы с целью напоминания выводятся на экран. Выделяются значения, которые нам необходимы. Далее напоминается формула суммы синуса аргумента, которая используется при дальнейшем решении примера. На завершающем этапе подставляются конкретные значения из таблицы, и получается ответ.
Второй пример предлагает упростить некоторое сложное выражение, содержащее тригонометрические функции. Для ее решения используются обе формулы, рассмотренные ранее. Решение демонстрируется пошагово. Чтобы школьники понимали, откуда берутся значения, выводится таблица тригонометрических значений и выделяются используемые ячейки.
В итоге, как и в предыдущем примере, выводится ответ.
Третий пример является аналогичный первому, а четвертый, приведенный далее с решением, является более сложным и интересным. Необходимо найти косинус суммы аргумента, если известны некоторые данные. Задачу предпочтительно рассмотреть с учителем либо репетитором. Если ученик является сообразительным и с хорошей математической базой, то он сможет разобраться и самостоятельно в том случае, если пропустил урок или хочет его восстановить в памяти. Для того чтобы закрепить понимание подобных примеров, можно предложить школьникам некоторые другие аналогичные примеры из школьного учебника, при решении которых им будет необходимо использовать формулы синуса и косинуса суммы аргументов.
Пятый пример по сложности занимает первое место. В нем предлагается решить тригонометрическое уравнения, для чего необходимо хорошо помнить и понимать, как необходимо использовать тригонометрические формулы.
Решение приводится очень понятным и подробным способом. Диктор объясняет каждый шаг, не упустив ни один важный момент. С правой стороны от решений приводятся выноски и формулы, которые применяются при выполнении данного задания.
С помощью данного видеоурока школьники смогут самостоятельно в домашних условиях повторить тему, которую проходили в школе, подготовиться к грядущим самостоятельным работам.
ТЕКСТОВАЯ РАСШИФРОВКА:
Мы уже познакомились с тригонометрическими функциями, их графиками, научились решать тригонометрические уравнения. А сейчас приступим к изучению тригонометрических формул, с помощью которых будем преобразовывать тригонометрические выражения.
В тригонометрии самыми важными являются формулы, которые обычно называют синус суммы и косинус суммы.
sin(x + y) = sin x cos y + cos x sin y,
cos (x + y) = cos x cos y - sin x sin y.
Эти формулы можно прочитать так: синус суммы двух углов равен сумме между произведением синуса первого угла и косинусом второго угла и произведением косинуса первого угла и синуса второго угла;
косинус суммы двух углов равен разности между произведением косинусов этих углов и произведением суммы этих углов.
Из этих формул мы сможем вывести практически все формулы тригонометрии.
Как же использовать формулы синуса суммы и косинуса суммы. Рассмотрим примеры, учитывая, что каждая формула может применятся как «слева направо», так и «справа налево».
ПРИМЕР 1. Вычислить sin 105°.
Решение. Представим сто пять градусов как сумму 105°= 45° + 60°. Нам известно, что sin 45°= cos 45°= , sin 60°= , cos 60°= .
Показать таблицу значений
Подставим эти значения в формулу синуса суммы
sin(x + y) = sin x cos y + cos x sin y,
Тогдаsin 105°= sin( 45° + 60°) = sin 45° cos 60°+ cos 45° sin 60°= ∙ + ∙ = = .
(синус ста пяти градусов равен синусу суммы сорока пяти градусов и шестидесяти градусов и равна эта сумма дроби, в числителе которой сумма корня из двух и корня из шести, а в знаменателе - четыре.)
Ответ: sin 105°=.
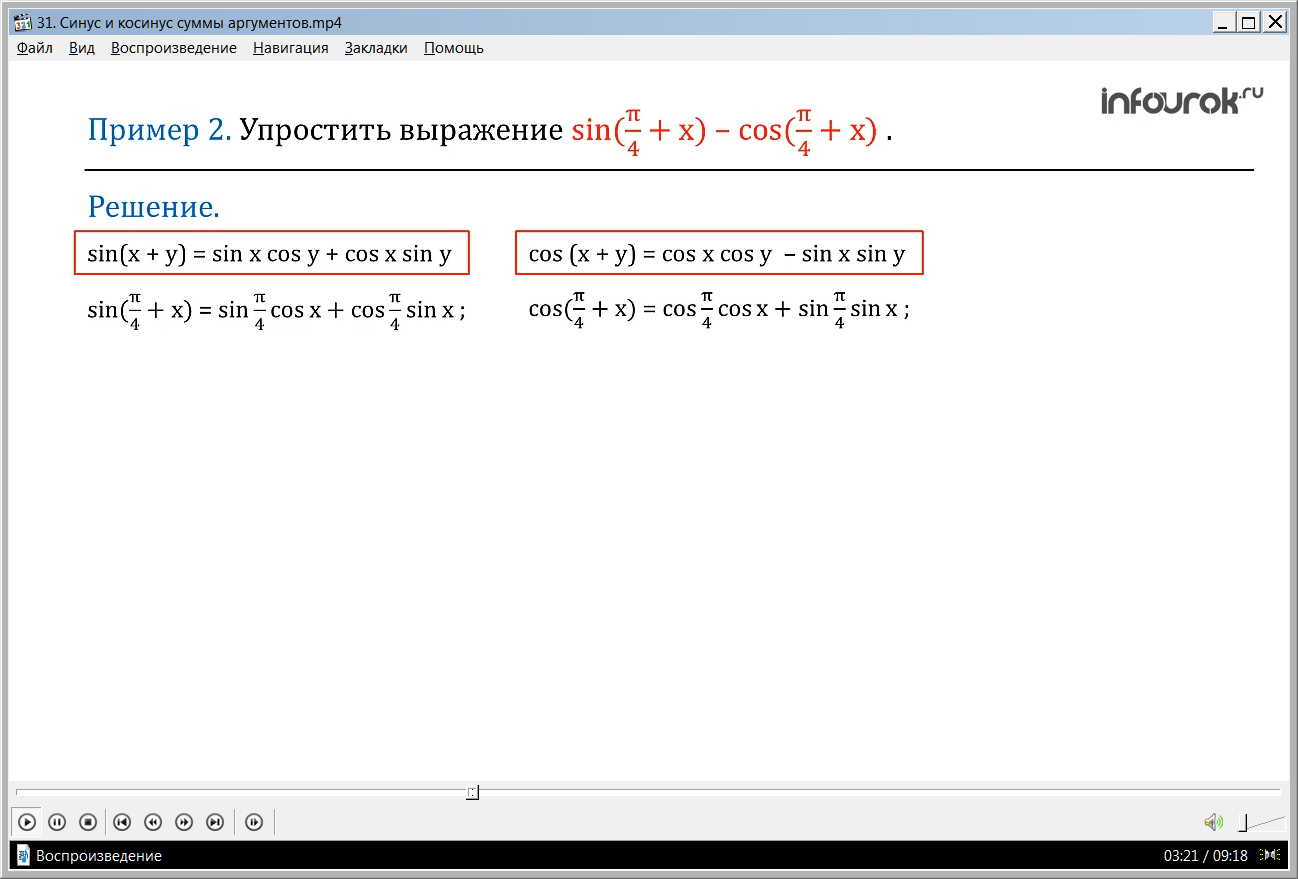
ПРИМЕР 2. Упростить выражение sin ( + х) - cos ( + х) (разность синуса пи, деленное на четыре, плюс икс и косинуса пи, деленное на четыре, плюс икс).
Решение. Применим формулу синуса суммы для уменьшаемого sin ( + х)
sin(x + y) = sin x cos y + cos x sin y,
Тогда уменьшаемое sin ( + х) = sin cosх + cos sinх .
Применим формулу косинуса суммы для вычитаемого cos ( + х)
cos (x + y) = cos x cos y - sin x sin y.
Вычитаемое cos ( + х) = cos cosх + sin sinх
Получим
sin (+ х) - cos (+ х) = sin cos х + cos sin х - cos cos х + sin sin х
Показать таблицу значений
Из таблицы значений найдем значение sin и cos
sin=, cos=, подставим эти значения в выражение и получим:
= ∙ cosх + ∙ sinх - ∙ cosх + ∙ sinх
∙ cosх – ∙ cosх = 0, остается ∙ sinх + ∙ sinх что равно 2 ∙ ∙ sinх получаем sinх.
sin ( + х) - cos ( + х) = sin cos х + cos sin х - cos cos х + sin sin х =
= ∙ cos х + ∙ sin х - ∙ cos х + ∙ sin х = 2 ∙ ∙ sin х = sin х. Это полное числовое решение.
Ответ: sin ( + х) - cos ( + х) = sinх.
ПРИМЕР 3. Вычислить sin 17° cos 13° + cos17° sin 13°. (синус семнадцати градусов, умноженный на косинус тринадцати градусов плюс косинус семнадцати градусов, умноженный на синус тринадцати градусов).
Решение. Данное выражение можно «свернуть» в синус суммы аргументов 17° и 13°(т.е. применить формулу синуса суммы «справа налево»).
sin(x + y) = sin x cos y + cos x sin y,
Получим
sin cos 13° + cos sin 13° = sin ( + 13°) = sin 30° = ( сумма произведения синуса семнадцати градусов на косинус тринадцати градусов и произведения косинуса семнадцати градусов на синус тринадцати градусов равно синусу суммы семнадцати и тринадцати градусов равно синусу тридцати градусов равно одной второй).
Ответ: .
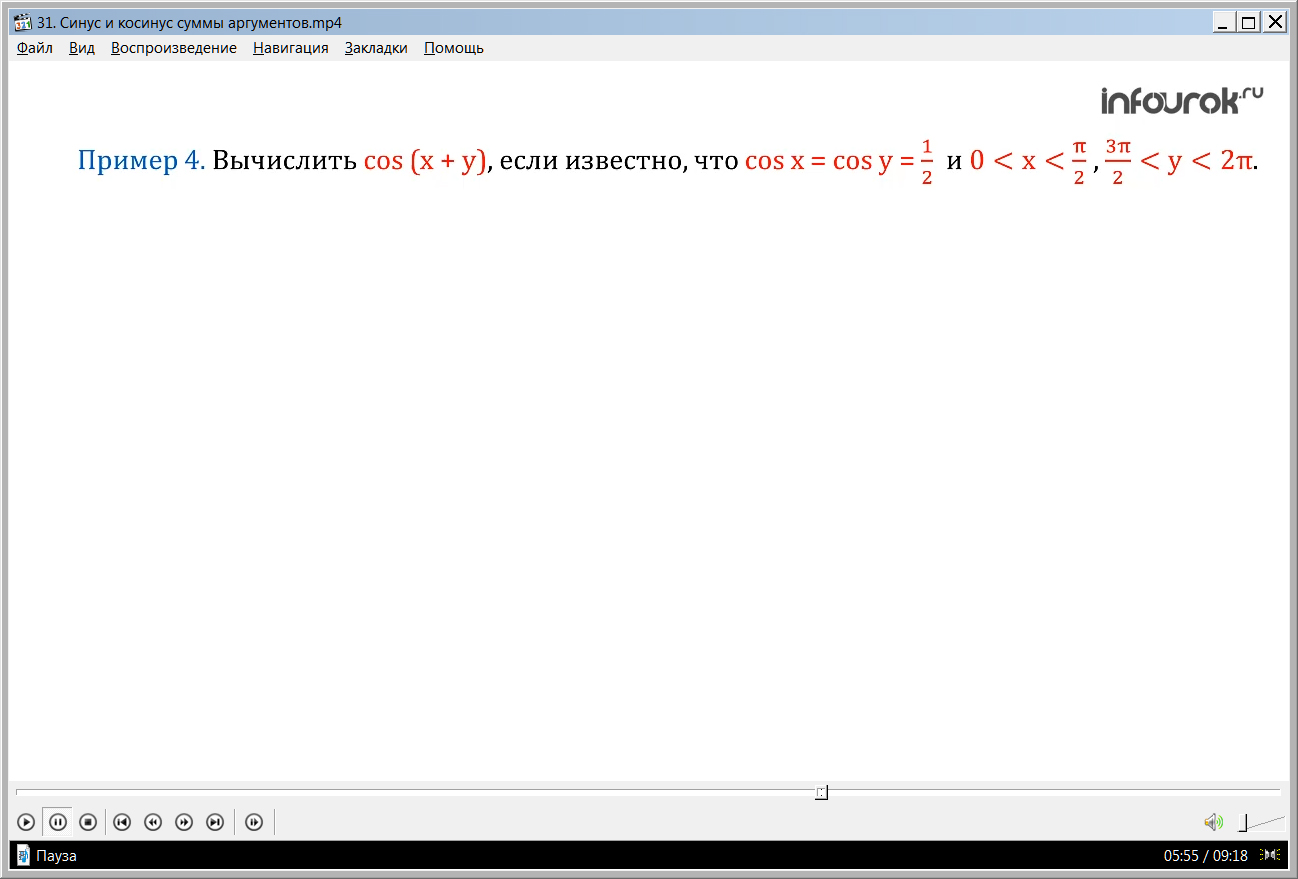
ПРИМЕР 4. Вычислить cos (х+ у), если известно, что cos х = cos у = и
0 х (икс больше нуля и меньше пи на два), у 2π (игрек больше трех пи на два, но меньше двух пи).
Решение. Воспользуемся формулой косинуса суммы:
cos (x + y) = cos x cos y - sin x sin y.
Значения cosx и cosy заданы. Вычислим значения sinx и siny. Воспользуемся основным тригонометрическим тождеством: sin2t + cos2t = 1. Имеем: sin2x = 1 - cos2х , а так как cos х = , то подставим в формулу и получим = 1 – ()2 = 1 - = .
sin2x = 1 - cos2х = 1 - = Это полное числовое решение.
По условию аргумент икс принадлежит первой четверти, а в ней синус положительный. Поэтому sinх = .
Аналогично, sin2 у = 1 - cos2у = 1 - = , но аргумент игрек принадлежит четвертой четверти, а в ней синус отрицательный, поэтому sin у = - .
Подставив полученные и заданные значения в формулу косинуса суммы, получим cos (x + y) = ∙ - ∙ = + = 1.
Ответ: 1.
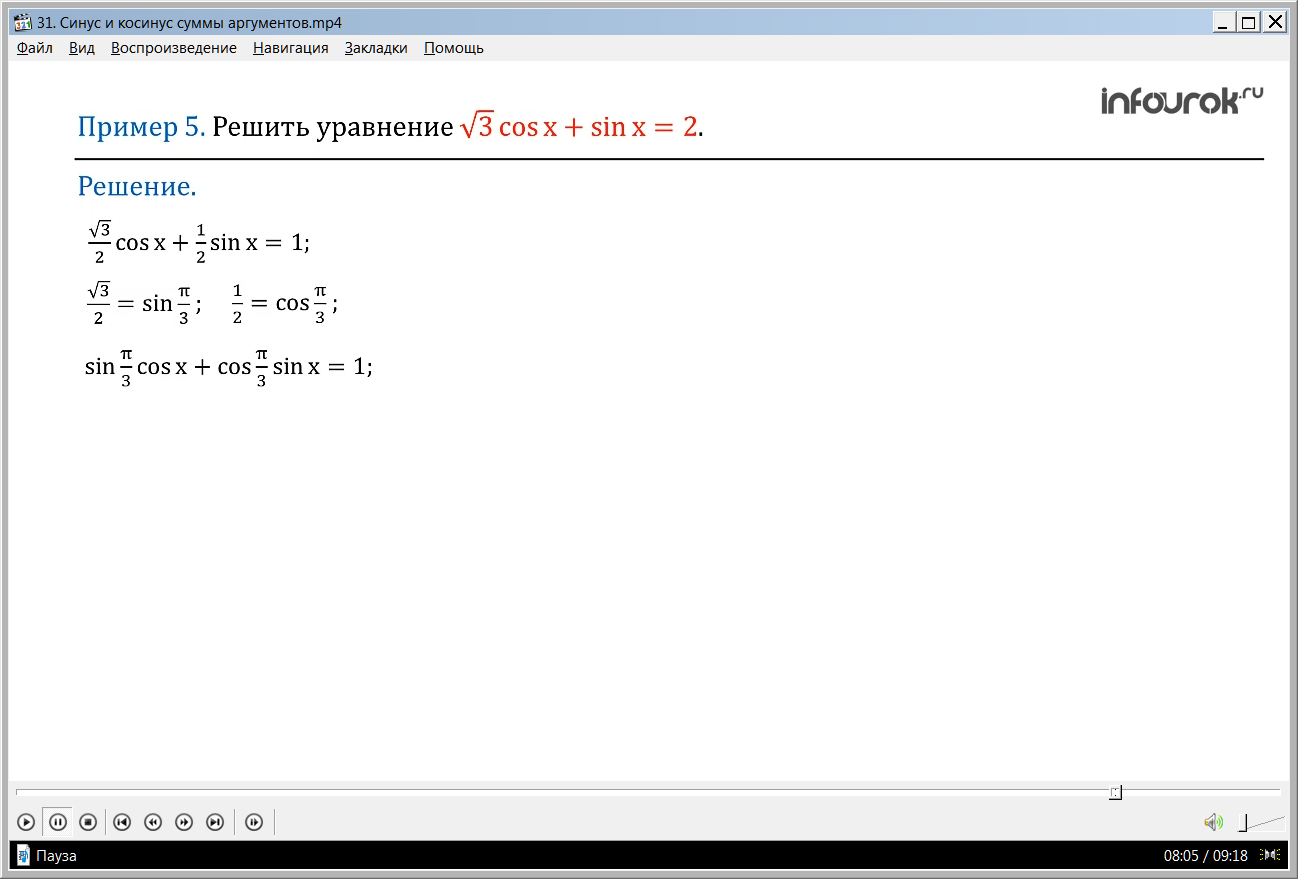
ПРИМЕР 5. Решить уравнение cosx + sinx = 2.
Решение.
Разделим обе части уравнения на два, получим cosx + sinx=1
Приведем данное уравнение к виду формулы синуса суммы двух углов:
и вспомним, что = sin , а = cos .
Показать таблицу значений
cos x + sin x = 1,
sincos x + cos sin x = 1,
Тогда выражение в левой части уравнения представляет собой правую часть формулы синус суммы для аргументов и х. Таким образом выражение левой части будет равно sin (+ х)
Преобразуем уравнение
sin ( + х) = 1,
Используя определение решения элементарного тригонометрического уравнения sint = a при а= 1, имеем t = + 2πn,
где для нашего уравнения: а=1, t= + х, получим
+ х = + 2πn,
Находим значение х
х = – + 2πn,
х = + 2πn.
Ответ: х = + 2πn.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7711 |
| Номер материала | 844 |