
Урок "Синус, Косинус, Тангенс"

Краткое описание документа:
Видеоурок «Синус, косинус, тангенс» служит наглядным пособием для представления учебного материала по данной теме. В ходе урока рассмотрены понятия синуса, косинуса, тангенса, таблица основных значений синуса, косинуса и тангенса. Усвоение данного материала является важным, так как в дальнейшем он будет использоваться во многих областях математики, и ее разделов, посвященных тригонометрическим функциям. Поэтому применение наглядного материала, способствующего более глубокому усвоению понятий, целесообразно и желательно. Задача данного видеоурока – облегчить усвоение материала, способствовать запоминанию понятий, формировать умение их применять в дальнейшем при решении задач.
В видеоуроке используются инструменты, помогающие сконцентрировать внимание ученика на изучаемом предмете. При помощи анимации выполняемые построения повторяют привычные действия у доски. При этом четкие построения хорошо видны всем ученикам. Важные детали выделяются цветом. Сочетание анимированного представления и голосового сопровождения дает возможность освободить учителя от подачи стандартного блока материала. Освободившееся время можно использовать для улучшения индивидуальной работы. Таким образом, при помощи видеоурока можно повысить эффективность обучения.
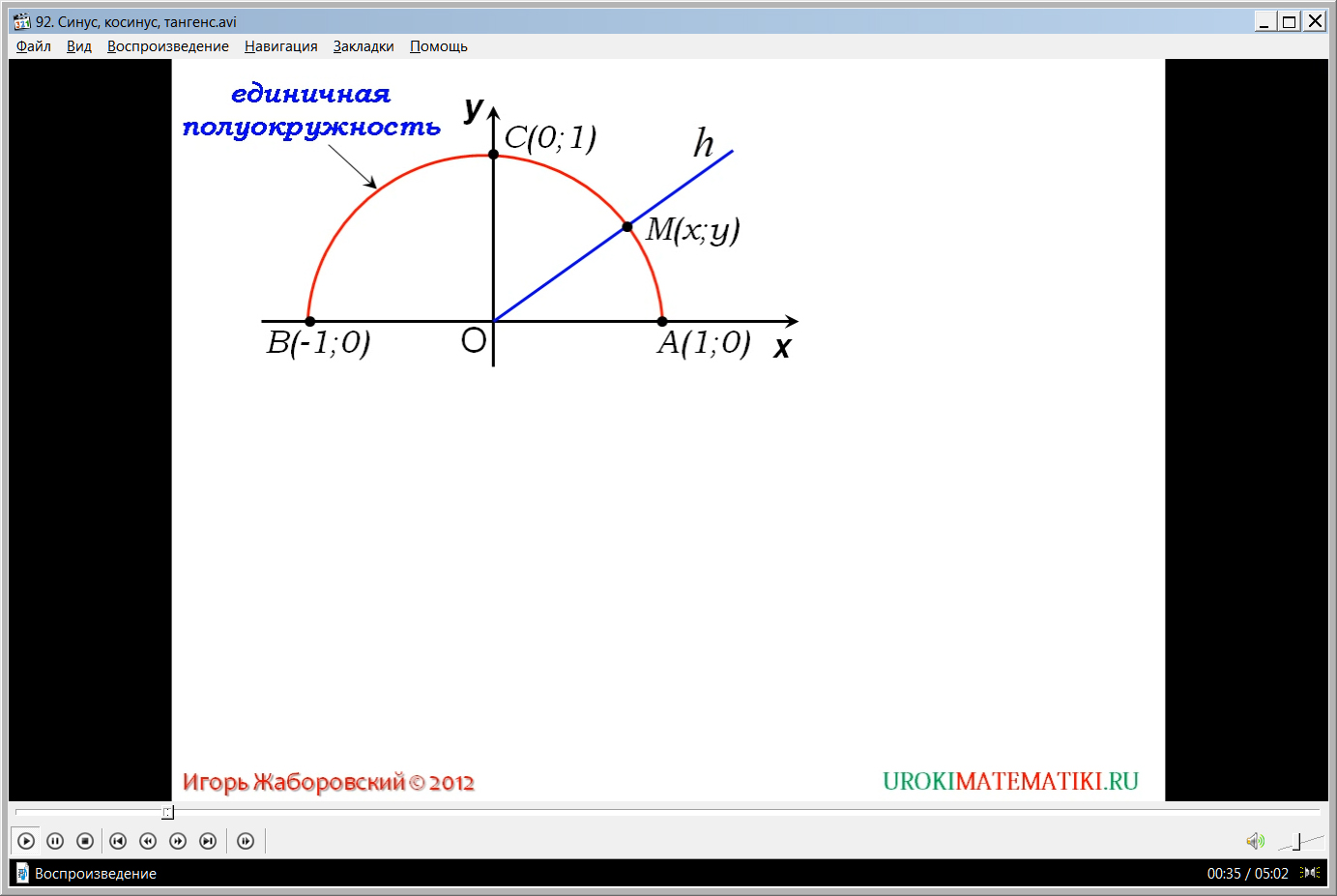
Видеоурок начинается с представления темы и построения. На экране представлена прямоугольная система координат ХОУ. В данной системе координат строится половина окружности с центром в точке (0;0). Полуокружность располагается в первой и второй четвертях координатной плоскости и пересекает оси координат в точках А(1;0), В(-1;0) и С(0;1). Окружность такого вида называется единичной окружностью. Название окружности вынесено на экран и выделено цветом для запоминания.
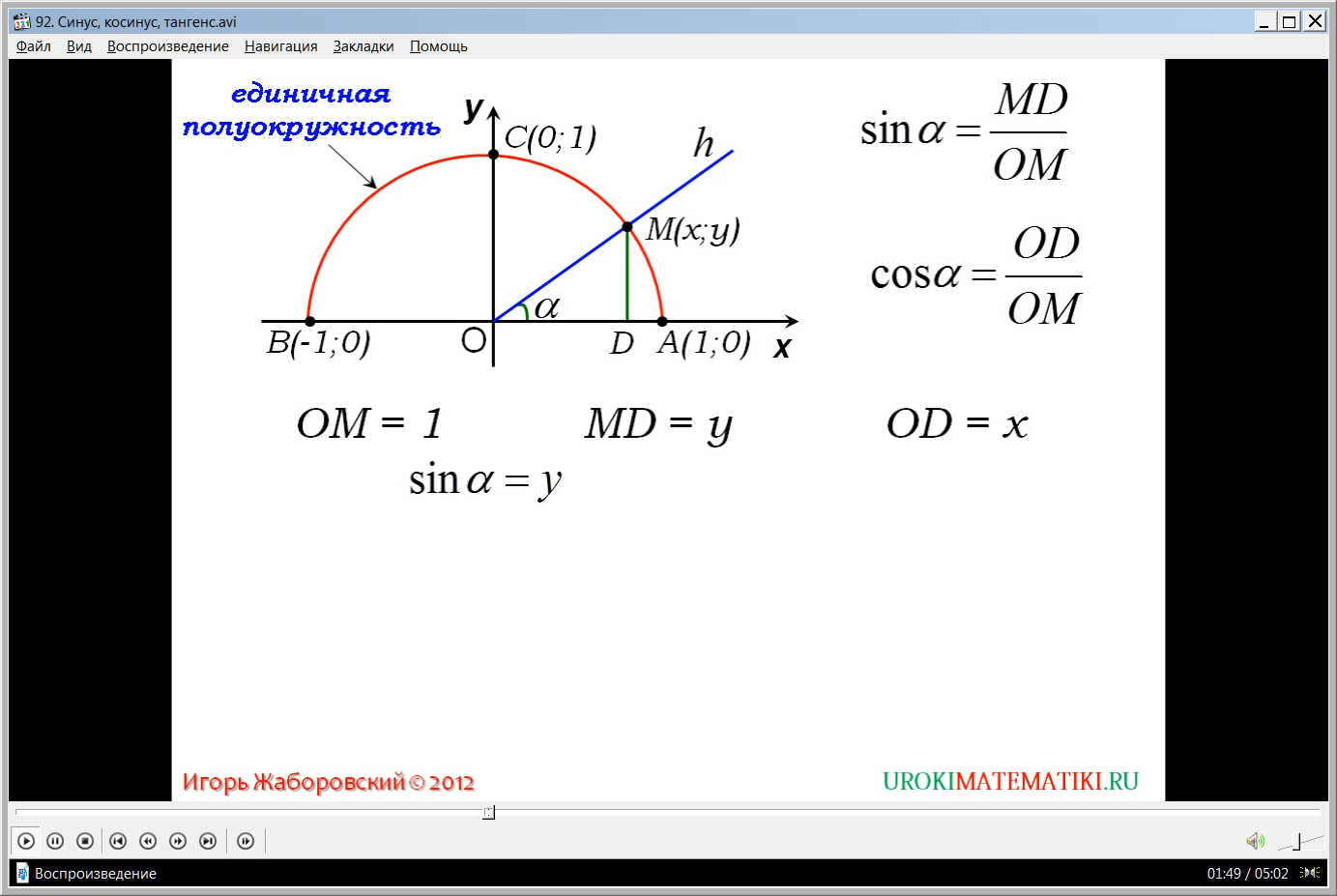
Из начала координат строится луч h, пересекающий единичную окружность в некоторой точке М(х;у). Отмечаем угол, образованный лучом h и положительной полуосью абсцисс ∠α. При совпадении луча h с положительной полуосью ОХ угол ∠α=0. Когда угол ∠α острый, можно из точки М(х;у) опустить перпендикуляр на положительную полуось ОХ. При этом синус угла ∠α будет равен отношению построенного перпендикуляра MD к радиусу ОМ, то есть sinα= MD/ОМ. Это соответствует уже имеющимся знаниям учеников о понятии синуса как отношения противолежащего катета прямоугольного треугольника к гипотенузе. Также ученикам напоминается, что косинус угла – это отношение прилежащего катета к гипотенузе. Согласно этому, косинусом угла ∠α является отношение OD к ОМ, то есть cosα= OD/ОМ.
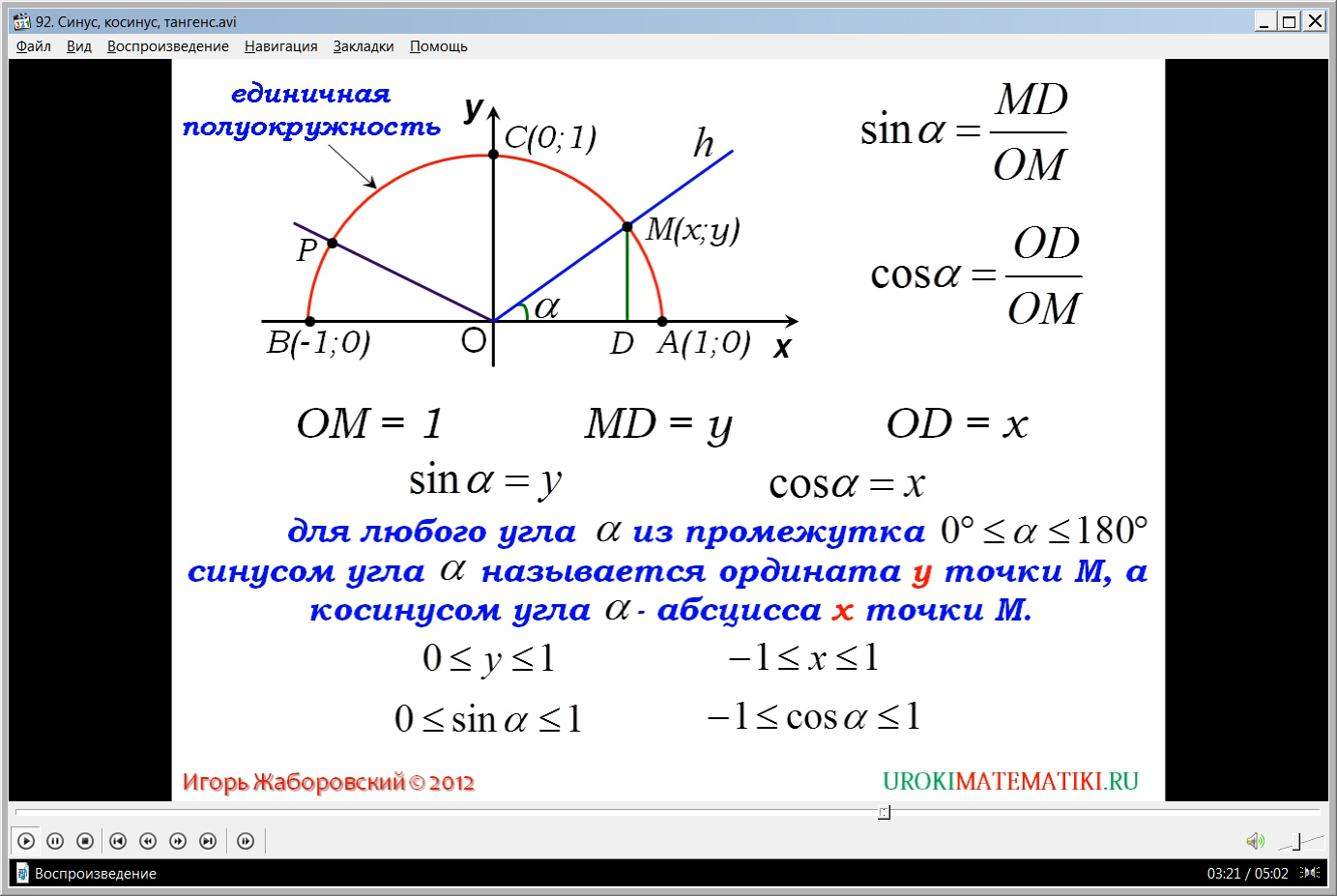
В данном случае рассматривается единичная окружность, поэтому гипотенуза, равная радиусу, равна ОМ=1. А MD и OD в данной системе координат определяются координатами точки М(х;у). Поэтому MD=у, а OD=х. после подстановки данных значений в выражения, определяющие синус и косинус угла ∠α, получим sinα=у, а cosα=х. Из этого можно сделать вывод, что синус острого угла равен ординате точки М, принадлежащей единичной окружности, а косинус острого угла равен абсциссе точки М.
В случаях, когда образованный угол является прямым или развернутым, то синус и косинус угла также может определяться данными формулами через координаты. На рисунке приводятся примеры таких углов – прямой угол ∠АОС, тупой угол ∠АОР, а также развернутый угол ∠АОВ. Общее правило для всех этих углов формулируется на экране и выделяется цветом. Оно утверждает, что для всякого угла α, входящего в промежуток 0°<= α<=180°, синус является ординатой у точки М, а косинус является абсциссой данной точки. Также рассматривается область определения ординаты у и абсциссы х. Так как мы строили единичную окружность, то в рассматриваемой части координатной плоскости у принимает значения от 0 до 1, то есть 0<=у<=1. При этом х принимает значения от -1 до 1, то есть -1<=х<=1. Поэтому для рассматриваемого множества углов, которые расположены в промежутке от 0° до 180°, можно утверждать, что синус угла принимает значения 0<= sinα <=1, а косинус принимает значения -1<= cosα <=1.
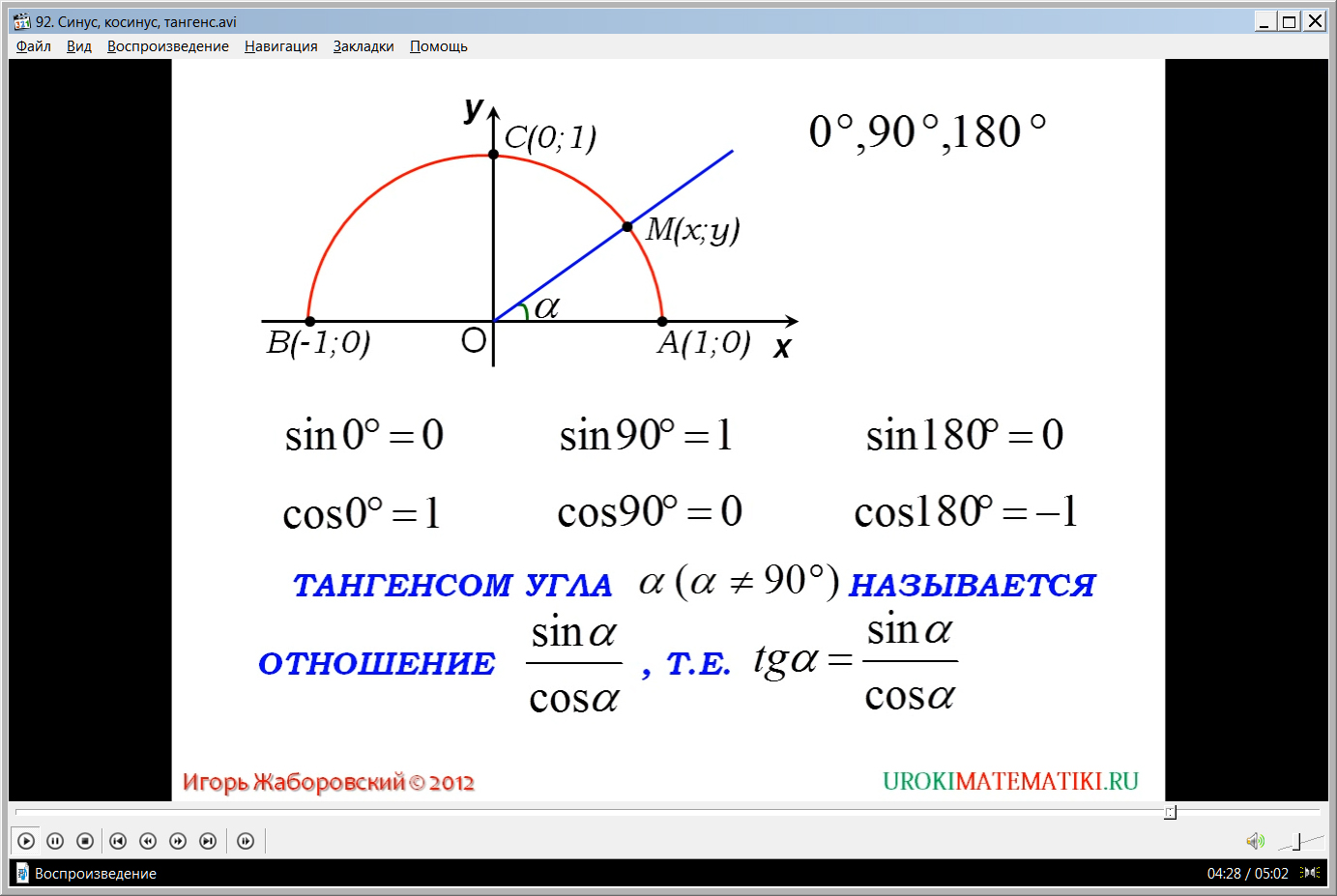
Далее рассматривается нахождение значений для углов 0°, 90°, 180°. Таким углам соответствуют углы, образованные положительной полуосью ОХ с лучами ОА, ОС, ОВ. Синусы и косинусы данных углов определяются координатами точек А, С, В. Поэтому можно говорить о том, что sin0°=0, sin90°=1, sin180°=0, cos0°=1, cos90°=0, cos180°=-1.
Также в области рассмотренных свойств рассматривается и понятие тангенса угла α, который не равен α≠90°. Отмечается, что тангенс угла α равен отношению tgα=sinα/ cosα. А в случае, когда α=90°, тангенс не определен, так как в косинус данного угла равен 0. Подставив значения синуса и косинуса в выражение, получаем запрещенное деление на ноль. Поэтому из рассматриваемого ряда углов можно говорить только о tg0°=0 и tg180°=0.
Видеоурок «Синус, косинус, тангенс» может применяться в школе при ведении традиционного урока. Также данный материал будет полезен ученикам, желающим самостоятельно освоить предмет или углубить его понимание. Наглядное пособие также поможет учителю донести особенности изучаемого предмета ученику в ходе дистанционного обучения.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 4198 |
| Номер материала | 768 |