
Урок "Система линейных уравнений с тремя переменными"

Краткое описание документа:
В математике существует определение уравнения с тремя переменными. До этого, в прошлых видеоуроках, мы рассматривали, как правило, уравнения с одной или с двумя неизвестными. В решении большинства задач подобных конструкций вполне достаточно. Однако в некоторых случаях требуется знания свойств линейных уравнений и с тремя переменными.
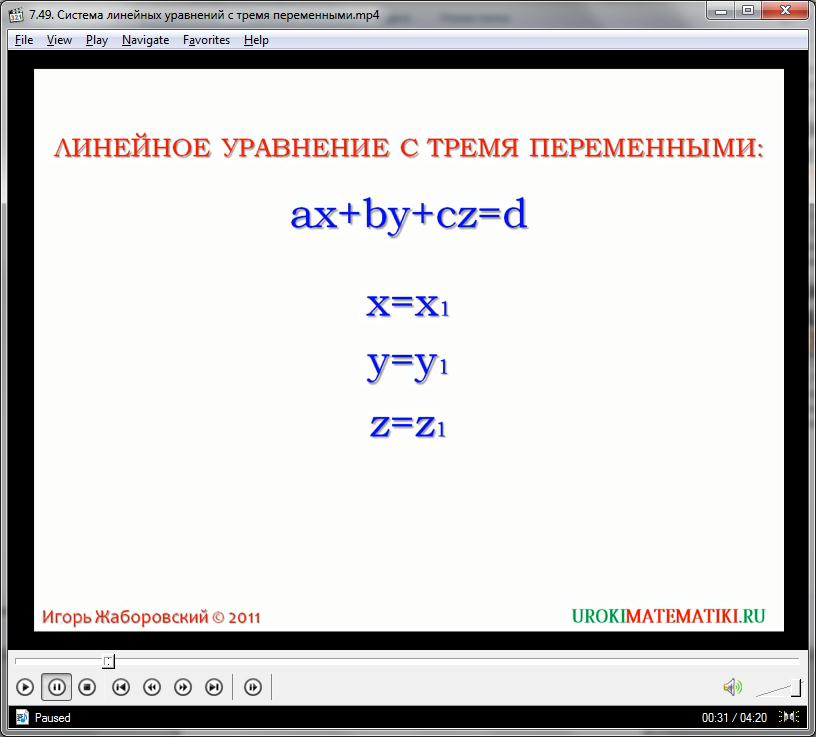
Рассмотрим абстрактный пример:
ax + by + cz = d
Это линейное уравнение с тремя переменными x, y, и z, включающее свободный член d, и коэффициенты при переменных a, b, и c. Само по себе, подобное уравнение редко когда бывает полезным. Оно не может быть представлено в виде простой функциональной зависимости, и не имеет решения напрямую, если неизвестны две, и более переменных.
Однако трехпеременные уравнения играют большую роль при решении системы линейных уравнений, состоящих из трех равенств.
Обычно, системы уравнений включают лишь два выражения, представляющих взаимосвязь между х и у в разных ракурсах. Добавление третьего уравнения позволяет ввести и третью переменную, которая связана с х и у определенной зависимостью.
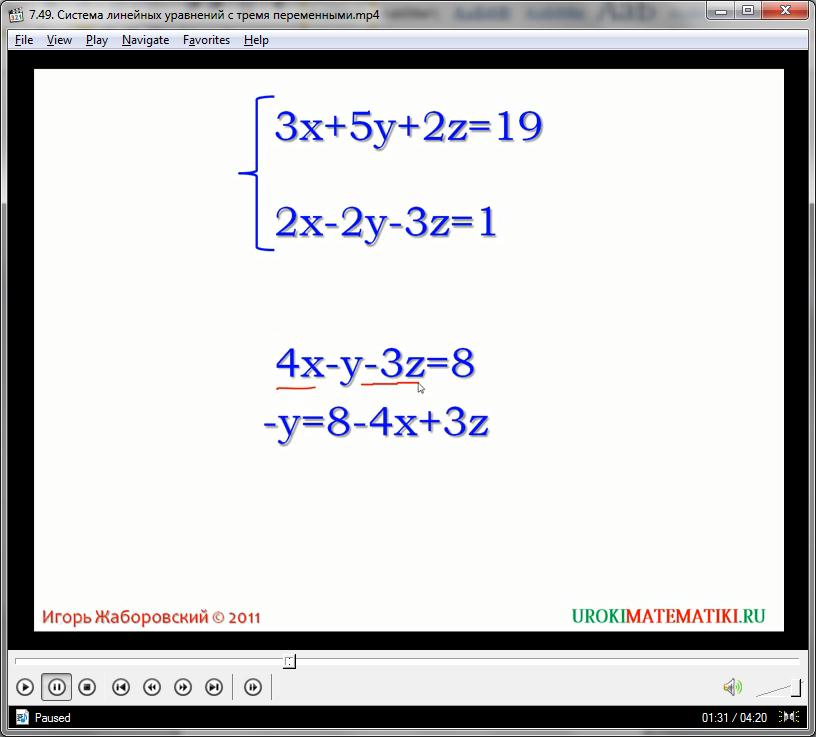
Иначе говоря, линейная система уравнений с тремя неизвестными – это три взаимосвязанных равносильных уравнения, каждое из которых содержит три неизвестные переменные. Соответственно, корнями подобной системы называется такая тройка чисел, при введении которой вместе х, у и z все три уравнения приобретут форму правильного равенства. Решение любой подобной системы проводится при помощи метода подстановки, или путем сложения. Рассмотрим практический пример. Найти корни системы уравнений вида:
3х + 5у + 2z = 19
2х – 2у – 3z = 1
4х – у – 3z = 8
Используя третье уравнение, выразим значение у через остальные переменные:
4х – у – 3z = 8
-у = 8 – 4х + 3z
у = -8 + 4х – 3z
Исключив одну переменную, определив её значение, можно подставить его в два других уравнения, получив, таким образом, систему из двух уравнений с двумя неизвестными:
3х + 5у + 2z = 19
2х – 2у – 3z = 1
у = -8 + 4х – 3z
3х + 5(-8 + 4х – 3z) + 2z = 19
2х – 2(-8 + 4х – 3z) – 3z = 1
Раскрываем скобки, приводим подобные слагаемые, сокращаем противоположные значения:
3х + 5(-8 + 4х – 3z) + 2z = 19
2х – 2(-8 + 4х – 3z) – 3z = 1
3х – 40 + 20х – 15z + 2z = 19
2х + 16 – 8х + 6z – 3z = 1
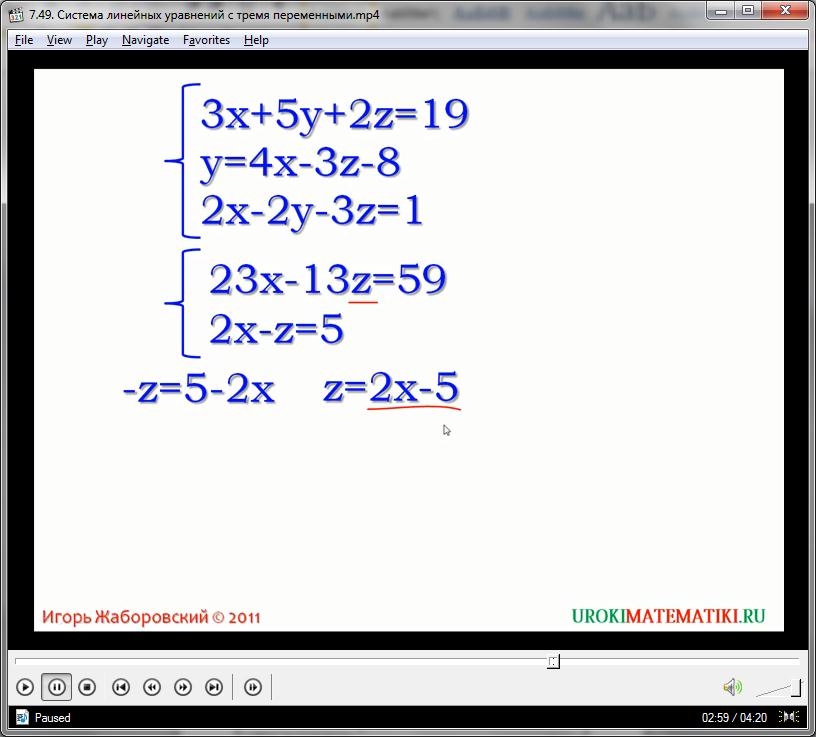
23х – 13z = 59
-6х + 3z = -15
Для упрощения второго выражения проводим деление обеих частей равенства на -3:
2х – z = 5
Откуда выражаем переменную z, как:
2х = 5 + z
z = 2х – 5
Подставляем значение z в уравнение 23х – 13z = 59, решаем его:
23х – 13z = 59
z = 2х – 5
23х – 26х + 65 = 59
-3х = -6
х = 2
Нам удалось найти первый корень для нашей системы трехпеременных уравнений. Подставляем его в любое удобное уравнение для вычисления z: логичней пользоваться короткой формой z = 2х – 5, ведь применяя тождественные преобразования, мы получаем абсолютно равносильные выражения. Находим вторую переменную:
z = 2х – 5
х = 2
z = 4 – 5 = -1
Теперь можно найти у, подставив соответствующие значения известных переменных в следующее выражение:
у = -8 + 4х – 3z
х =2
z = -1
у = -8 + 8 + 3 = 3
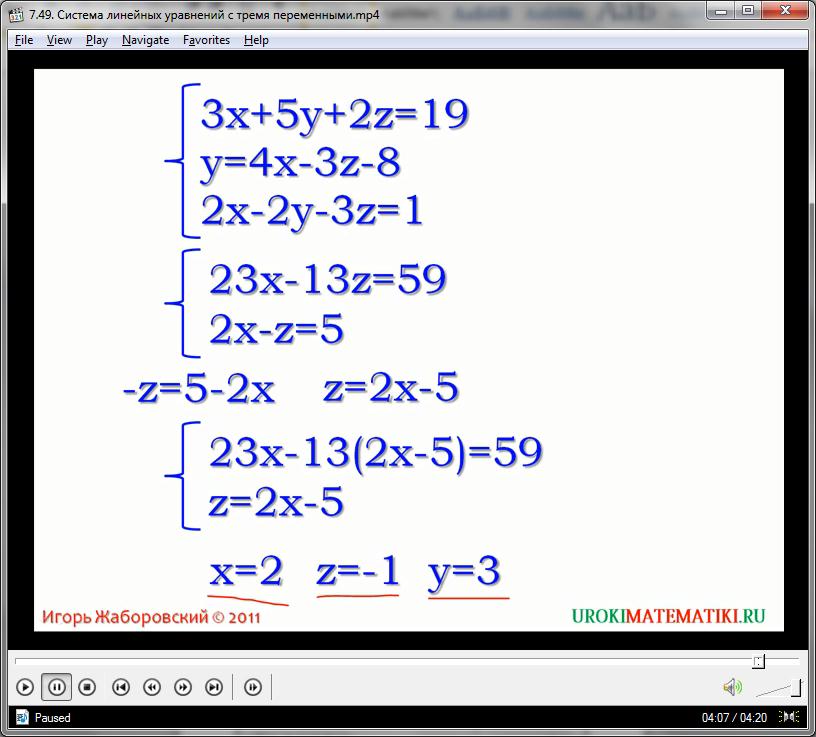
Таким образом, мы получили все три корня для данной системы уравнений – это тройка чисел 2, 3, -1.
Следует отметить, что система уравнений, которая включает три выражения, должна равномерно содержать все три переменных в каждом равенстве. Иначе с нахождением корней могут быть принципиальные проблемы.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5006 |
| Номер материала | 481 |