
Урок "Решение задач с помощью систем уравнений"

Краткое описание документа:
Как уже упоминалось, системы линейных уравнений с двумя переменными очень часто встречаются при решении различных тривиальных задач. В таких случаях применение системы позволяет либо значительно сократить ход задачи, связав воедино два разных участка её условия, либо же решить такую задачу, ответ которой может быть найден исключительно через взаимосвязанную пару уравнений.
Как же применять систему при решении практических упражнений? Для этого, как наглядно показывает наше видео, необходимо задать через переменные х и у неизвестные (но искомые) элементы задачи. Далее, ориентируясь по условию, нужно составить соответствующую систему уравнений с участием неизвестных х и у.
Например, система линейных уравнений часто помогает справиться с упражнением, связанным с нахождением некоторых чисел, причем в условиях так или иначе описана взаимосвязь между этими числами. Рассмотрим пример.
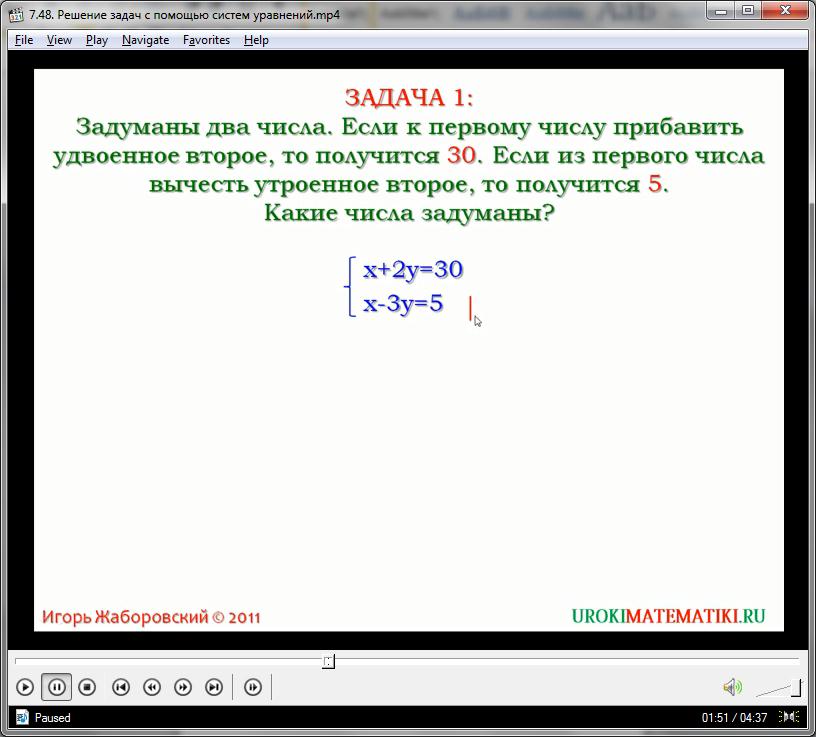
Даны два числа. Известно, что если к первому числу прибавить удвоенное второе, то получится число 30. Если же из первого вычесть утроенное второе, то в итоге будет 5. Иначе говоря, в первом случае имеем сумму чисел, причем второе слагаемое будет удвоенным, и эта сумма равна 30. Зададим первое число как х, второе – как у, и запишем первое уравнение:
х + 2у = 30
Не забываем, что второй элемент удвоен, и коэффициент у равен потому двойке. Также можно сказать, что разность первого числа и утроенного второго равна пяти. Математически можно выразить так:
х – 3у = 5
Так как числа у нас одни и те же, мы вправе не только воспользоваться прежними переменными х и у, но можем связать наши уравнения в систему, причем корни этой системы будут представлять собой два искомых числа. Итак, имеем систему вида:
х + 2у = 30
х – 3у = 5
Это довольно простая система, которую можно решить всеми тремя способами. Воспользуемся методом подстановки. Обозначим х во втором уравнении (потому что, в данном выражении получатся положительные значения у):
х – 3у = 5
х = 5 + 3у
Подставляем данное выражение переменной х в первое уравнение:
х + 2у = 30
х = 5 + 3у
5 + 3у + 2у = 30
5у = 30 -5 = 25
у = 5
Мы определили, что одно из наших чисел равно 5. Найдем вторую переменную, а именно – х, через имеющееся выражение:
х = 5 + 3у
у = 5
х = 5 + 15 = 20
Таким образом, корнями данной системы уравнений является пара 20, 5. И наши искомые числа – это именно 20 и 5.
Через применение систем легко решать упражнения на нахождение возможности, и доказательства тождеств. Например, решим такую задачу.
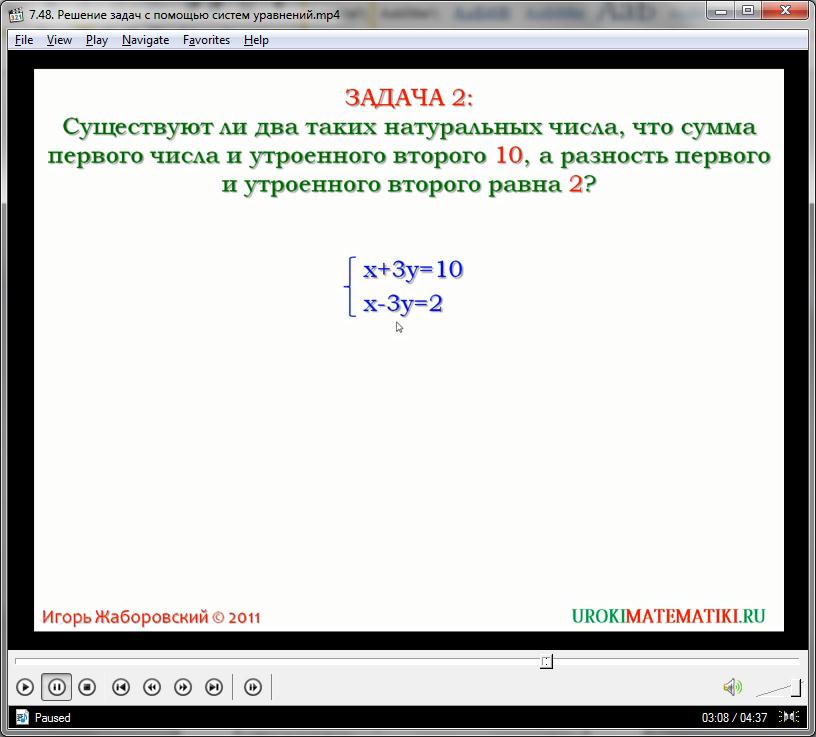
Существует ли пара натуральных чисел, которые в сумме первого и утроенного второго дадут десять, а разность первого и утроенного второго будет равна двум?
Чтобы решить данную задачу, составим систему линейных уравнений на основании имеющегося условия. Представим, что действительно существуют такие натуральные числа, которые бы соответствовали задаче. Обозначим их за х и у. Как известно по условию, второе число фигурирует утроенным, значит, в наших уравнениях будет одночлен 3у. Сумма переменной х с этим одночленом равна десяти, а разность – двум. Составляем два уравнения в системе:
х + 3у = 10
х – 3у = 2
Данную систему уравнений легче всего решить методом сложения, так как уже готовы сокращающиеся элементы 3у и -3у. Складываем почленно оба уравнения:
х + 3у = 10
+
х – 3у = 2
=
2х = 12
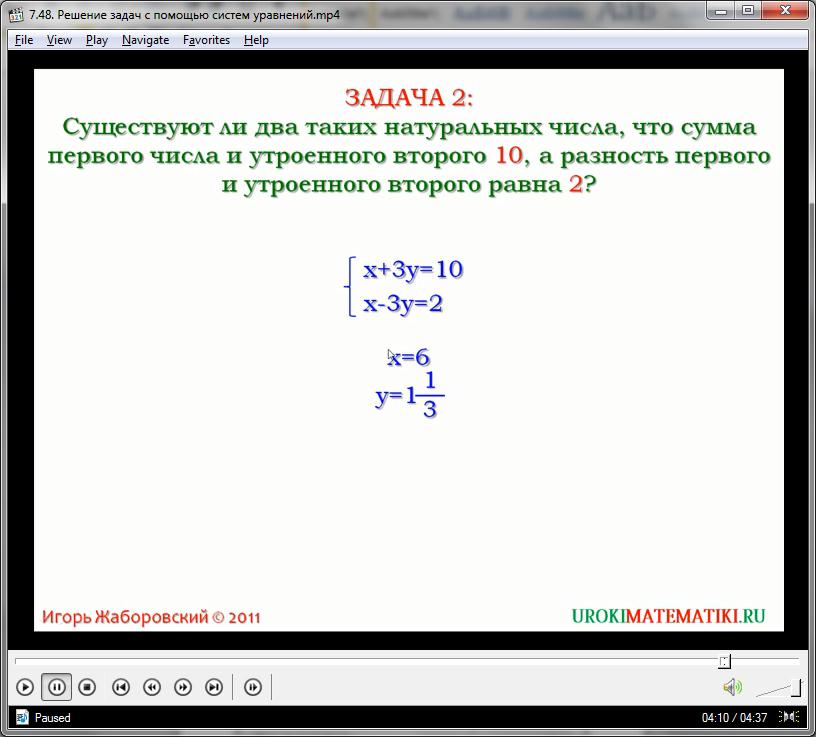
х = 6
Итак, один из корней мы нашли, он равен 6. Найдем у через любое уравнение:
х + 3у = 10
х = 6
6 + 3у = 10
3у = 10 – 6 = 4
у = 1(1/3)
Корнями данной системы являются числа 4 и 1(1/3) – это действительные натуральные и существующие числа, значит ответ на задачу: да, существуют.
После нахождения корней в случае решения подобных задач важно понять, что сами по себе переменные не являются ответом на упражнение, они лишь указывают на него. Нужно правильно трактовать условие, используя переменные, и вывести ответ. Иногда он совпадает со значением корней, а иногда и нет (в задачах на доказательство, например).
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6581 |
| Номер материала | 480 |