
Урок "Способ сложения"

Краткое описание документа:
Системы линейных уравнений, представленных двумя переменными, можно решать несколькими способами в зависимости от особенностей самой системы. Во многих случаях, выбора особо нет, и приходится решать тем, или иным способом, без каких-либо альтернатив. Например, графический метод позволяет решить лишь элементарные уравнения с небольшими целыми коэффициентами. Кроме того, он требует построения графиков в декартовой системе, что не очень удобно. Способ подстановки достаточно универсален, но иногда приводит к сложным расчетам. Чтобы их избежать, можно воспользоваться методом сложения. Он подходит далеко не во всех случаях, но, порой, может пригодиться и значительно сократить объем вычислений для нахождения корней системы уравнений.
Для начала вспомним, что собой представляют тождественные действия. Согласно аксиоматическим положениям алгебры, тождественные действия не должны приводить к изменению значения переменных, а также к нарушению принципа равенства. Можно произвести множество вспомогательных операций и получить вполне корректный результат – но равенства должны быть незыблемы при этом. Рассмотрим абстрактный пример:
а + с = 5
х + у = 10
У нас есть две пары чисел, сумма первых составляет 5, сумма вторых равна 10. Логично, что общая сумма будет 15:
а + с + х + у = 5 + 10 = 15
При этом суммы пар складываются. И все равенства вполне сохраняются, не затрагивая значений переменных. Иначе говоря, в математике допускается процесс сложения двух равенств, при котором левая часть первого равенства складывается с левой частью второго, образуя левую часть итогового выражения. То же самое происходит и с правой частью. Главное соблюдать преемственность частей и не спутывать одночлены между разными направлениями. Значение переменных, при этом, так же не изменится. Зато когда мы произвели сложение двух уравнений, можно привести подобные слагаемые, сократить лишние элементы и провести иные дополнительные манипуляции, которые поспособствуют решению.
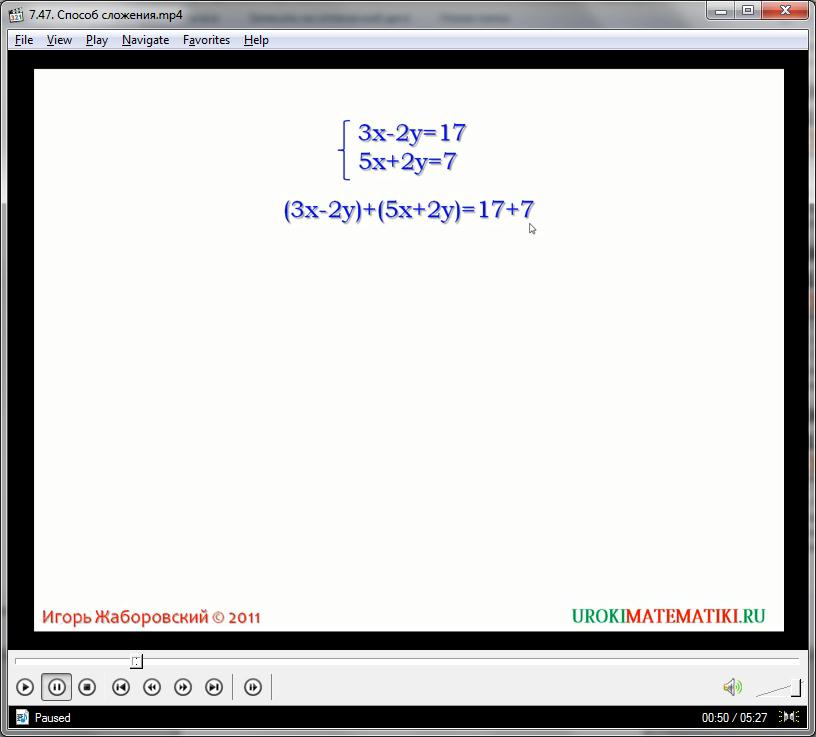
Рассмотрим систему вида:
3х – 2у = 17
5х + 2у = 7
Найдем корни этой системы, используя метод сложения. Почленно сложим каждую часть:
3х – 2у = 17
+
5х + 2у = 7
=
3х + 5х + 2у – 2у = 17 + 7
Приводим подобные, полностью сокращая переменную у, при этом получаем уравнение с одной неизвестной и решаем его:
8х = 24
х = 3
Подставляем полученное значение переменной х в любое уравнение из начальной системы:
3х – 2у = 17
х = 3
9 – 2у = 17
Решаем полученное уравнение с одной неизвестной у:
9 – 2у = 17
-2у = 17 – 9
-у = 4
у = -4
Таким образом, в ходе последовательных преобразований, при которых мы получили ряд равносильных уравнений, был определен корень системы в виде пары чисел 3 и -4.
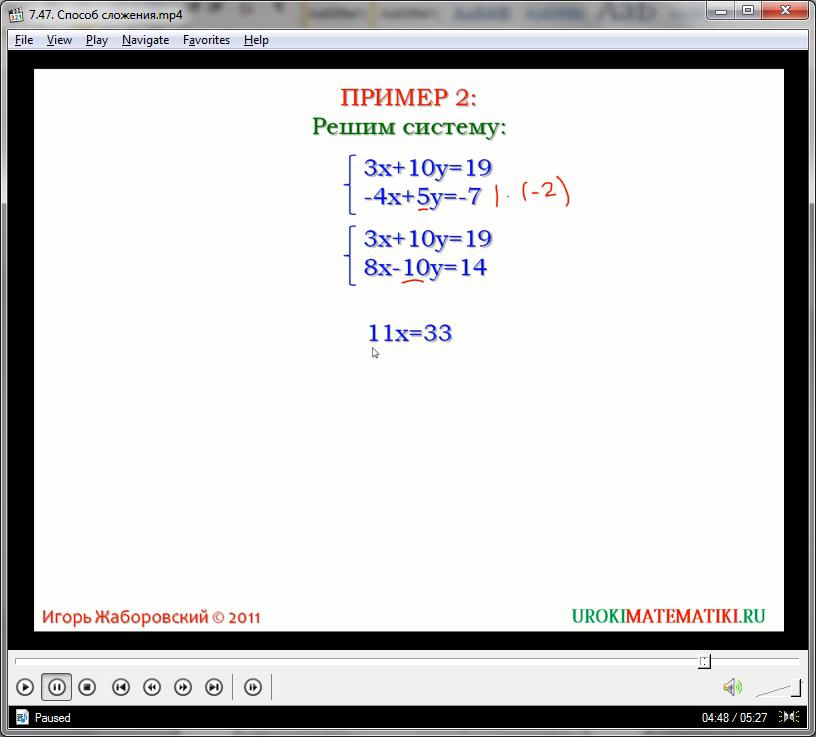
Чаще всего переменные не могут так просто сократиться. Тогда используют подгонку уравнения под параметры задачи путем умножения всего выражения на некоторое число. Алгоритм действий при решении системы линейных уравнений методом подстановки имеет вид:
- Подгоняем систему под возможное сокращение одной из переменных в процессе будущего алгебраического сложения. Для этого умножаем обе части выбранного уравнения на некоторое одинаковое число так, что бы переменная приобрела такой коэффициент, который был бы противоположным у этой же переменной во втором уравнении;
- Проводим почленное сложение обеих уравнений, при этом получаем итоговое равенство, в котором одна из переменных должна аннулироваться приведением подобных, если первый пункт выполнен правильно;
- Проводим тождественные преобразования, раскрываем скобки, приводим подобные слагаемые и решаем уравнение с одной неизвестной;
- Полученное выражение переменной подставляем в любое начальное уравнение, рассчитываем значение второй переменной по типу решения обычного уравнения с одной неизвестной;
- Проверяем полученную пару – необязательный пункт, который позволит удостовериться в правильности решения.
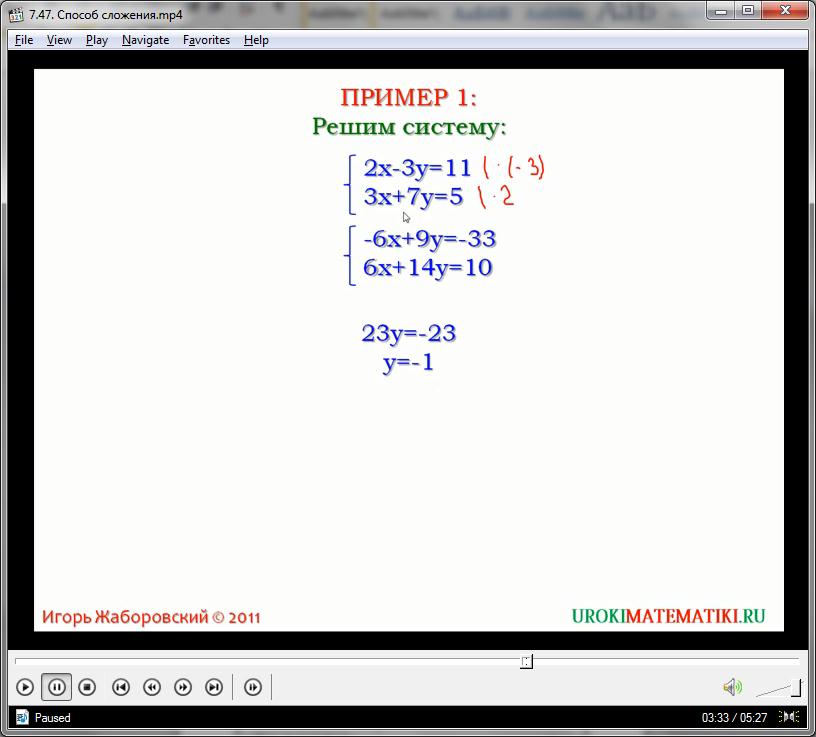
Решим систему уравнений, используя данный алгоритм:
2х – 3у = 11
3х + 7у = 5
Для того, чтобы сложить оба уравнения, сократив переменную х, необходимо умножить обе части первого выражения на -3, а второго – на 2:
(-3)(2х – 3у = 11)
(2)(3х + 7у = 5)
-6х + 9у = -33
6х + 14у = 10
Теперь можно сложить уравнения, сократив 6х:
-6х + 9у = -33
+
6х + 14у = 10
=
23у = -23
у = -1
Подставляем полученное значение в любое уравнение начальной системы и находим х:
2х – 3у = 11
у = -1
2х + 3 = 11
2х = 8
х = 4
Корнями данной системы является пара чисел 4 и -1.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6651 |
| Номер материала | 479 |