
Урок «Системы уравнений»

Краткое описание документа:
Для изучения сегодняшней темы нам необходимо вспомнить, какие способы решения систем уравнений с двумя переменными нам известны.
Для решения систем уравнений с двумя переменными использовались такие способы, как метод подстановки, алгебраического сложения, введения новых переменных, графический метод.
Сегодня на уроке мы рассмотрим несколько необычные применения этих методов, другие способы решения систем уравнений.
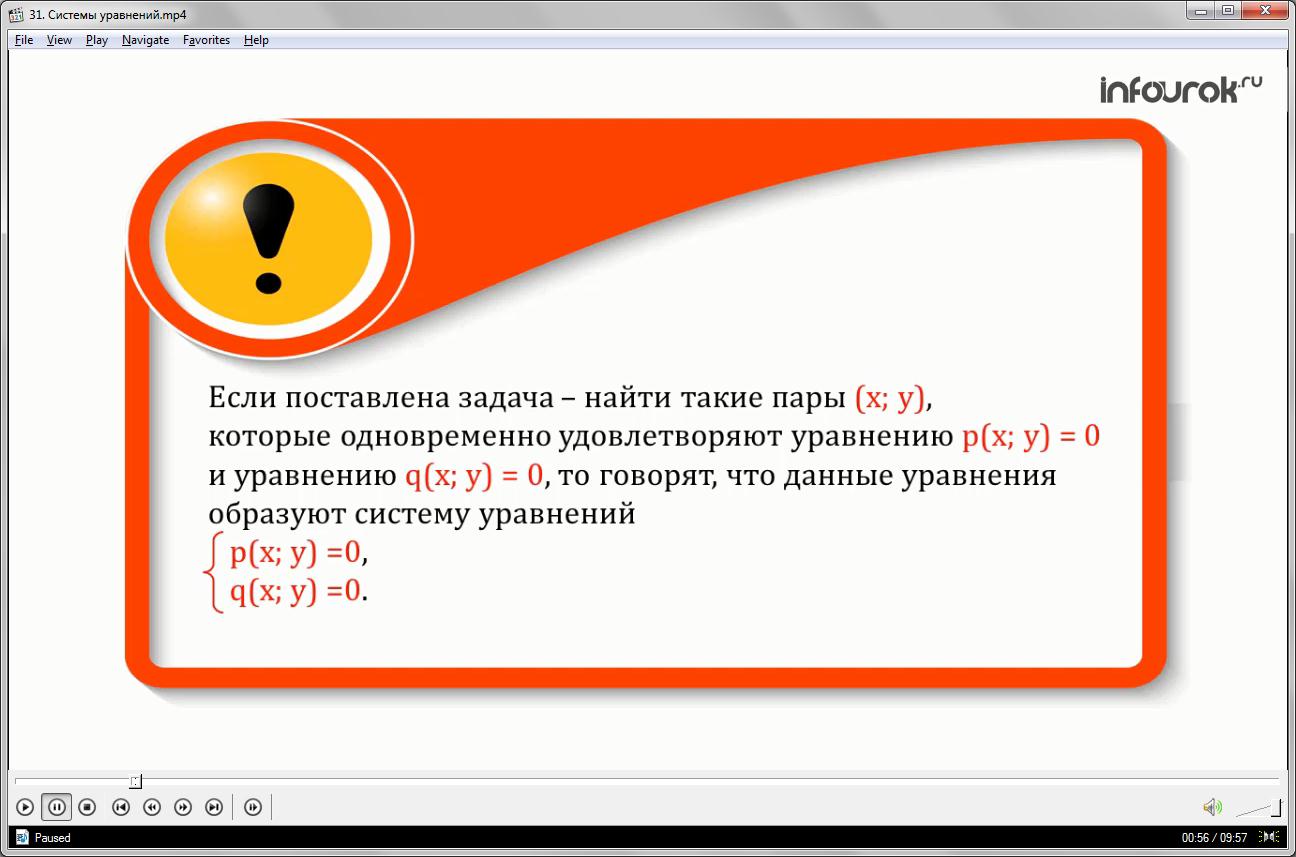
Определение первое. Если поставлена задача – найти такие пары икс и игрек, которые одновременно удовлетворяют уравнению пэ от икс игрек равно нулю и уравнению кю от икс игрек равно нулю, то говорят, что данные уравнения образуют систему уравнений :
пэ от икс игрек равно нулю
кю от икс игрек равно нулю
Определение второе.
Пару значенийикс и игрек, которая одновременно является решением и первого и второго уравнения системы, называют решением системы уравнений.
Определение третье.
Решить систему уравнений – значит найти все ее решения или установить, что решений нет.
По аналогии можно говорить и о системе трех уравнений с тремя неизвестными.
Пэ от икс игрек зэт равно нулю
Кю от икс игрек зэт равно нулю
эр от икс игрек зэт равно нулю
При этом надо найти тройки чисел икс игрек зэт, удовлетворяющие каждое уравнение системы. Вообще, можно говорить о системах с любым количеством уравнений и неизвестных.
Алгоритм решения системы уравнений прост: постепенный переход от сложного уравнения к более простому, но при этом выполнять равносильные преобразования.
Стремиться получить хотя бы одно линейное уравнение, а если происходит переход к уравнению-следствию, то обязательна проверка корней.
Определение четвертое.
Две системы уравнений называют равносильными, если они имеют одни и те же решения или решений не имеют.
Какие же способы решения систем уравнений являются равносильными?
Методы подстановки, алгебраического сложения, введения новых переменных приводят к равносильным преобразованиям
системы уравнений.
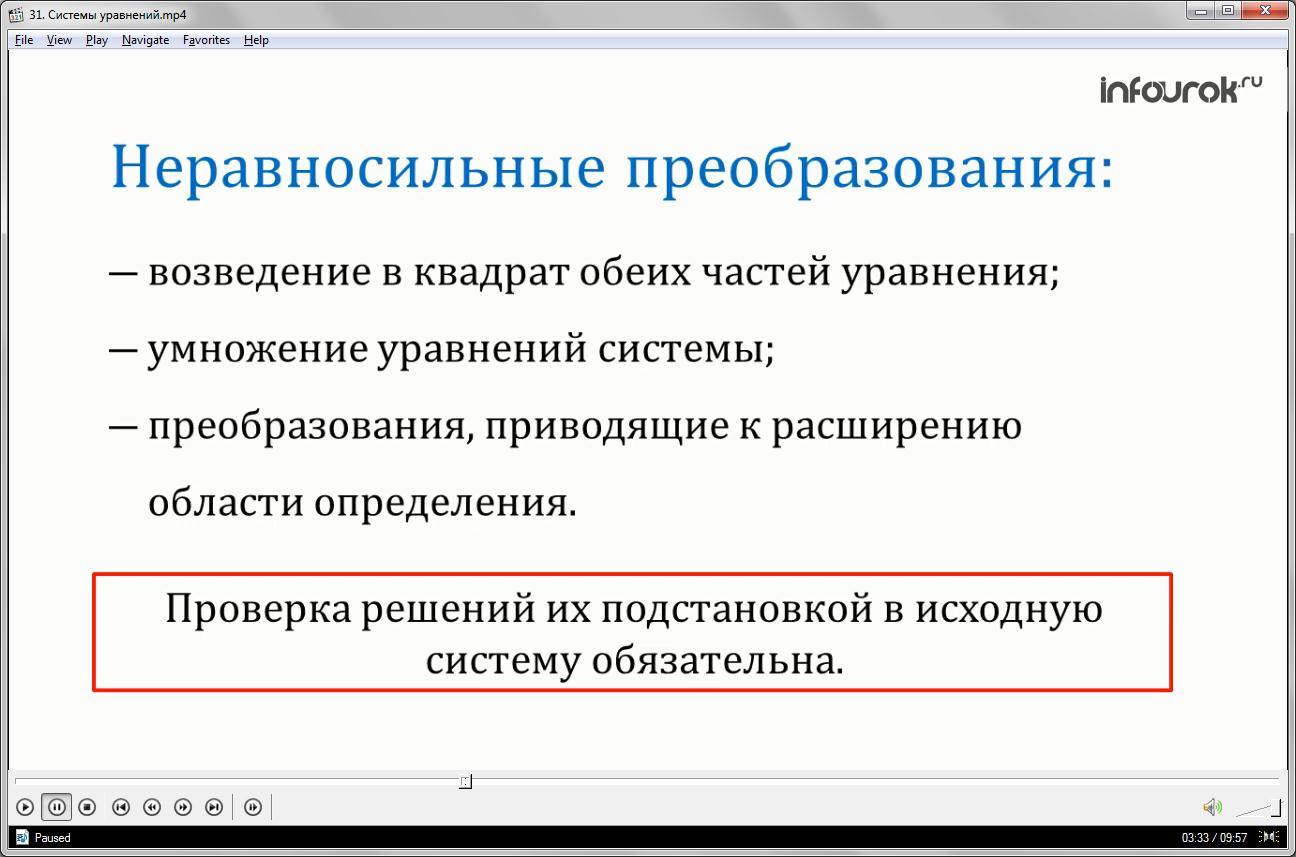
Запомните!
Если в процессе решения используются неравносильные преобразования хотя бы одного уравнения, к ним относятся возведение в квадрат обеих частей уравнения, умножение уравнений системы, преобразования, приводящие к расширению области определения, то необходима проверка решений их подстановкой в исходную систему.
Рассмотрим примеры.
Обратите внимание на рациональность решения системы.
Задание 1
Решить систему уравнений:
Первое уравнение — икс плюс игрек плюс два зэт равно четырем.
Второе уравнение – два икс плюс игрек плюс зэт равно единице.
Третье уравнение — икс плюс два игрек плюс зэт равно трем.
Решение
Можно заметить, что каждая переменная входит в систему четыре раза. Поэтому сложим все три уравнения (это равносильное преобразование) и получим: четыре икс плюс четыре игрек плюс четыре зэт равно восьми.
Разделим почленно обе части уравнения на четыре, получим: икс плюс игрек плюс зэт равно двум. В каждом уравнении системы будем выделять это равенство.
Тогда из второго уравнения системы имеем:
икс равен минус единице.
Из третьего уравнения получаем:
игрек равен единице.
Из первого уравнения имеем:
зэт равен двум.
Итак, система уравнений имеет единственное решение — тройку чисел: минус один, один, два. Решение в проверке не нуждается, так как преобразования выполнялись равносильные.
Ответ: тройка чисел: минус один, один, два.
Задание 2
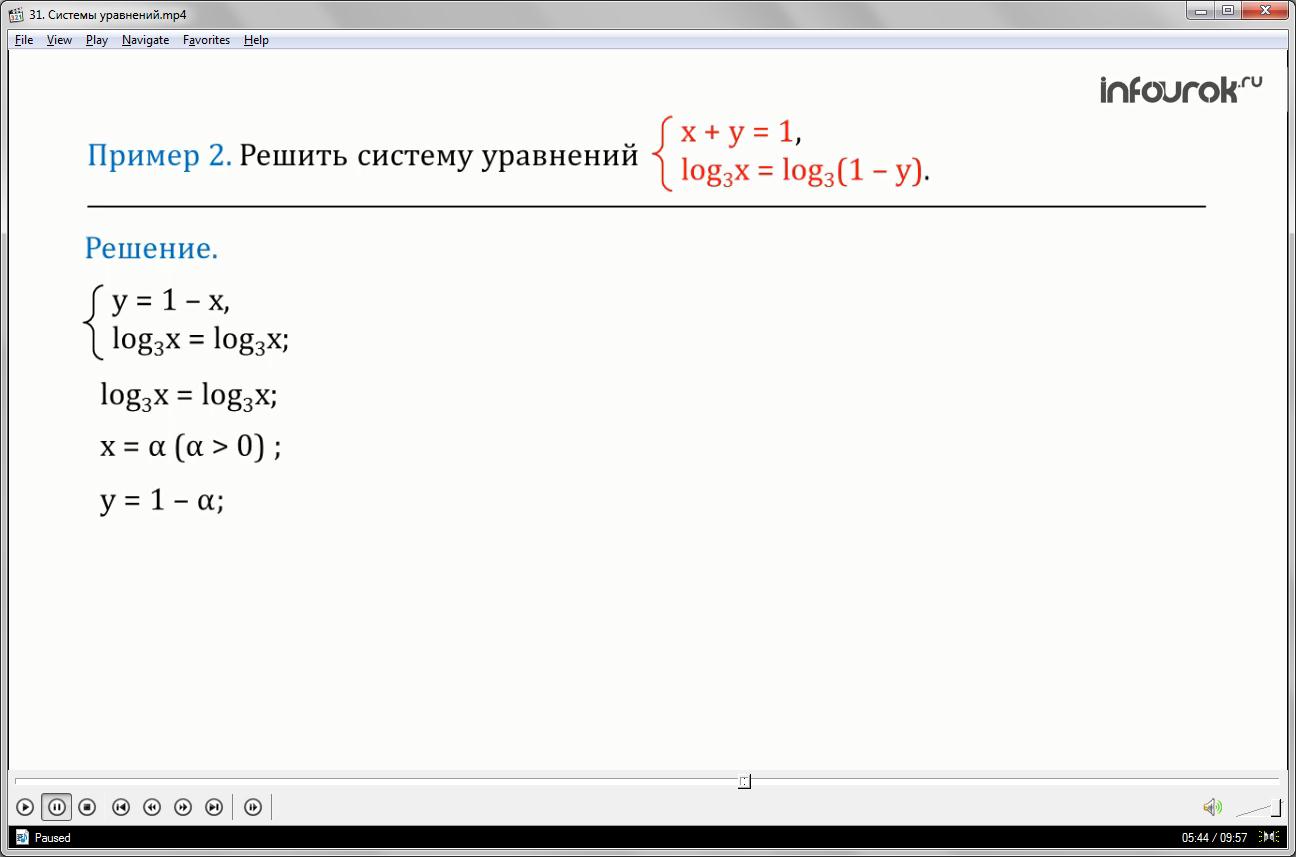
Решить систему уравнений
Первое уравнение – икс плюс игрек равно единице.
Второе уравнение логарифм икс по основанию три равно логарифму выражения один минус игрек по основанию три.
Решение
Выразим игрек через икс из первого уравнения системы и, подставляя его вместо игрека во второе уравнение, получаем уравнение: логарифм икс по основанию три равно логарифму икс по основанию три. Решениями этого уравнения являются все положительные числа. Каждому такому значению икс равное альфа, где альфа больше нуля, соответствует значение игрек равное один минус альфа. Следовательно, решениями исходной системы являются все пары чисел альфа и один минус альфа, где альфа — положительное число. Способ подстановки – равносильное преобразование.
Ответ: пара чисел: альфа и один минус альфа, где альфа — положительное число.
Задание 3
Решить систему уравнений: игрек квадрат плюс два икс игрек минус три икс квадрат равно нулю и игрек квадрат плюс три икс в квадрате равно четырем.
Решение
Можно заметить, что первое уравнение системы – однородное. Считая игрек неизвестной величиной, а икс – постоянной, решим его. Получим: игрек первое равно икс и игрек второе равно минус три икс.
Тем самым мы получили линейные уравнения. Исходная система сводится к совокупности двух систем уравнений:
первая система состоит из уравнений: игрек равен икс, игрек квадрат плюс три икс в квадрате равно четырем.
Вторая система состоит из уравнений: игрек равен минус три икс, игрек квадрат плюс три икс в квадрате равно четырем.
Решения первой системы — пара чисел: один и один и пара чисел: минус один, минус один. Вторую систему решаем способом подстановки.
Решениями системы является пара чисел: один, деленное на квадратный корень из трех и минус квадратный корень из трех, вторая пара: минус один, деленное на квадратный корень из трех и квадратный корень из трех.
При решении исходной системы все преобразования были равносильными, поэтому проверка не нужна.
Ответ: пара чисел: один и один; пара чисел: минус один, минус один; пара чисел: один, деленное на квадратный корень из трех, и минус квадратный корень из трех; пара: минус один, деленное на квадратный корень из трех, и квадратный корень из трех.
Задание 4
Решить систему уравнений
Первое уравнение – икс плюс игрек равно единице.
Второе — два икс в квадрате плюс два квадратных корней из икс минус икс равно игрек в квадрате минус один плюс два, умноженное на один плюс квадратный корень из икс.
Решение
Выразим игрек из первого уравнения и подставим во второе, перенесем во втором уравнении все члены в левую часть и, приведя подобные слагаемые, получим систему уравнений:
игрек равен один минус икс и икс в квадрате плюс икс минус два равно нулю.
Решением системы является пара чисел: один и ноль и пара чисел: минус два и три.
Эта система является следствием исходной, поэтому проверка обязательна.
Проверка
Проверим подстановкой в исходную систему уравнений, является ли каждая пара чисел решением данной системы.
Проверим первое уравнение.
Если икс равен единице, игрек равен нулю, то получаем верное равенство,
и во втором уравнении получаем
верное равенство. Значит, пара чисел: один и ноль — решение системы.
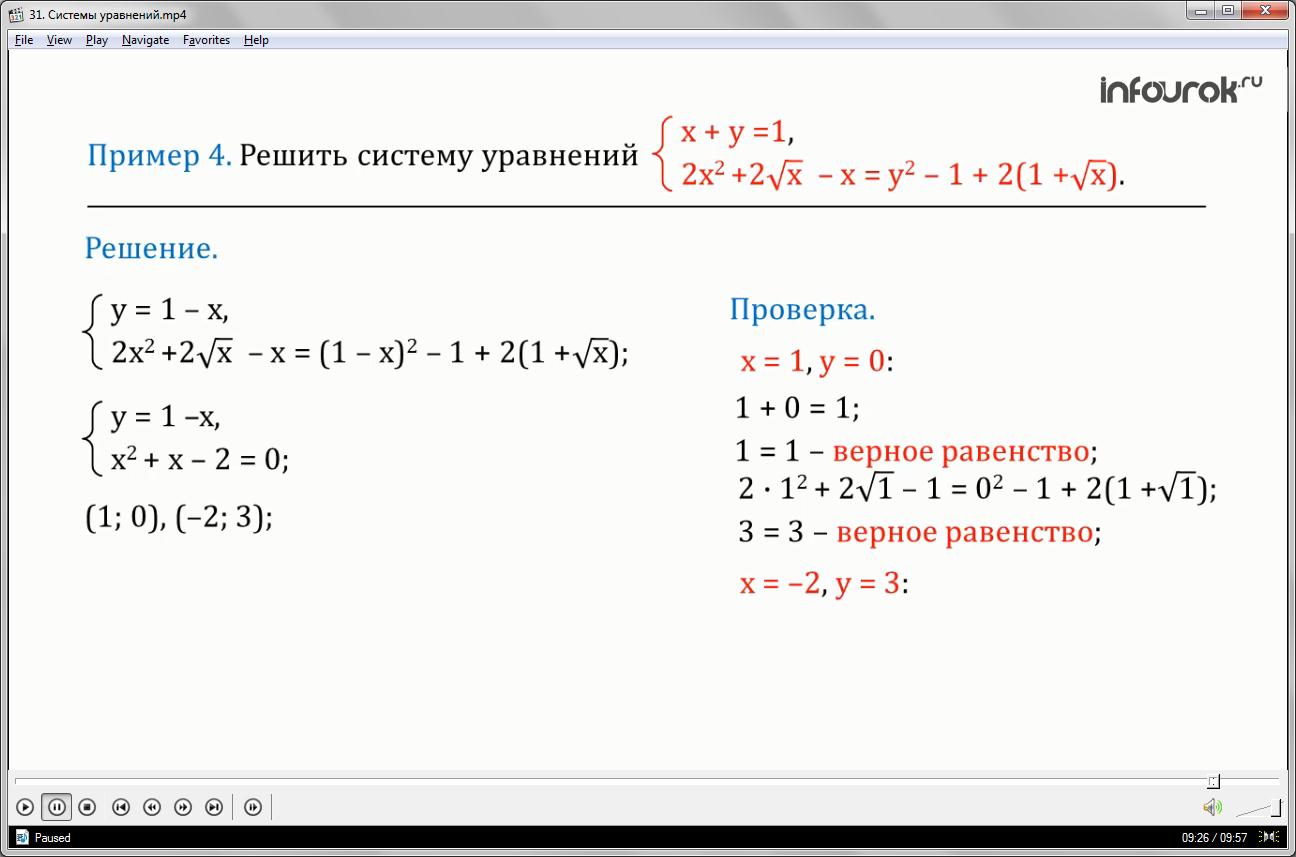
Проверяем вторую пару чисел: минус два и три. Если икс равен минус двум, игрек равен трем, то первое уравнение системы — верное равенство. А второе уравнение неверно, так как квадратный корень из минус двух не определён,
поэтому пара чисел: минус два и три не является решением системы.
Ответ: пара чисел: один и ноль.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6362 |
| Номер материала | 1080 |