
Урок "Скалярное произведение в координатах"

Краткое описание документа:
Видеоурок «Скалярное произведение в координатах» демонстрирует формулировку и доказательство теоремы о координатах скалярного произведения двух векторов, а также следствий этой теоремы. Данная тема важна для решения многих практических задач, поэтому ее необходимо хорошо усвоить, запомнить способ нахождения скалярного произведения в координатах, чтобы потом применять его при решении задач. Задача видеоурока как наглядного пособия по теме – облегчить усвоение и запоминание материала.

В видеоуроке используются анимационные эффекты, которые помогают запомнить понять ход рассуждений при доказательстве утверждений и запомнить формулировку теоремы, следствий из него. Важные детали доказательства и выводы при этом выделяются цветом, облегчая запоминание. Голосовое сопровождение, заменяющее объяснение учителя, в сочетании с хорошо структурированным видеоматериалом, дает возможность полностью заменить учителя при подаче стандартного блока учебного материала.
В начале видеоурока представляется его тема. Утверждается, что скалярное произведение векторов вычисляется также по координатам этих векторов. На экране демонстрируется формулировка теоремы, утверждающей, что в прямоугольной системе координат для векторов, выраженных координатами aˉ{x1;y1} и bˉ{x2;y2}, скалярное произведение определяется формулой aˉ·bˉ= x1x2+y1y2.

Доказательство теоремы начинается с рассмотрения ее для векторов, один из которых является нулевым. Очевидно, в этом случае произведение равно нулевому вектору 0ˉ. Действительно, при умножении каждой координаты aˉ=0ˉ или bˉ=0ˉ получаем произведение aˉ·bˉ=x1x2+y1y2=0ˉ. Затем рассматривается произведение в случае, когда каждый из векторов не равен нулю, то есть aˉ≠0, bˉ≠0. На экране из точки О к точкам А и В строятся векторы ОАˉ=аˉ и ОВˉ= bˉ. Неколлинеарность данных векторов означает, что при применении к ним теоремы косинусов АВ2=ОА2+ОВ2-2ОА·ОВ·cosα.
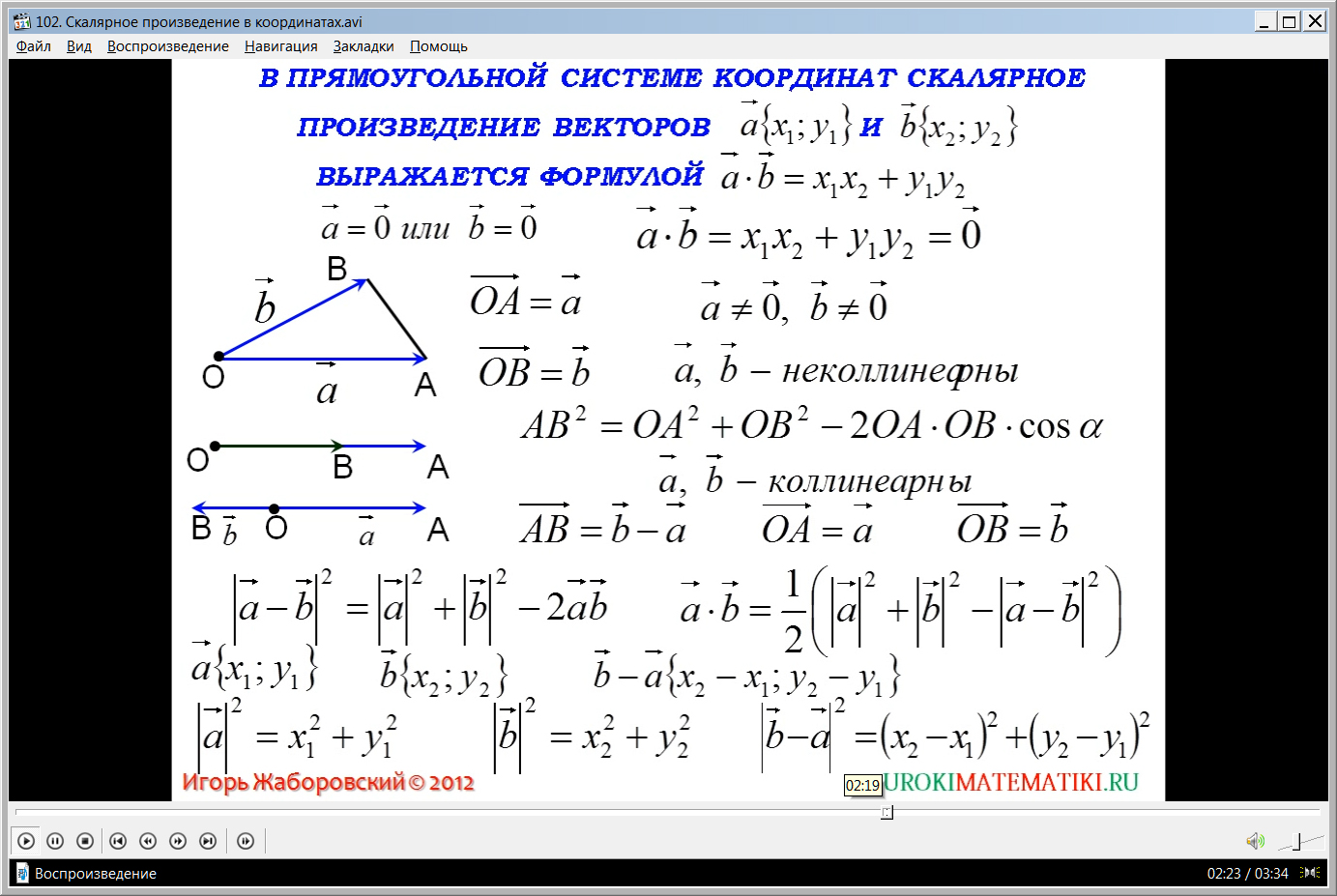
В случае коллинеарности векторов aˉ и bˉ указанное равенство в координатах также будет верно. На экране демонстрируется построение двух коллинеарных векторов aˉ и bˉ - сонаправленных и противоположно направленных. Отмечается, что в этом случае вектор АВˉ= bˉ- aˉ. ОАˉ=аˉ, ОВˉ= bˉ. По формуле скалярного квадрата для коллинеарных векторов |aˉ-bˉ|2=|aˉ|2+|bˉ|2-2aˉbˉ. Координаты векторов aˉ{x1;y1} и bˉ{x2;y2}, а вектора разности bˉ-aˉ{x2- x1;y2- y1}. Скалярный квадрат вектора aˉ равен квадрату длины вектора |aˉ|2= x12+y12. Скалярный квадрат вектора |bˉ|2= x22+y22. Квадрат вектора АВˉ вычисляется по формуле |bˉ-aˉ|2=( x2- x1)2+(y2- y1)2. Отмечается, что после преобразований данное выражение в формулу aˉ·bˉ=1/2(|aˉ|2+|bˉ|2-|аˉ-bˉ|2), в координатах также получается формула aˉ·bˉ=x1x2+y1y2.
Затем рассматриваются следствия из теоремы о координатах векторов. В первом следствии утверждается, что равенство нулю выведенной выше формулы aˉ·bˉ=x1x2+y1y2 для векторов aˉ{x1;y1} и bˉ{x2;y2} является необходимым признаком перпендикулярности этих векторов. Второе следствие дает возможность определить косинус угла между векторами aˉ и bˉ, используя формулу cosα=( x1x2+y1y2)/(√(x12+y12)·√(x22+y22). Доказывается справедливость данной формулы. Отмечается, что так как для скалярного произведения справедливо aˉ·bˉ=|aˉ|·|bˉ|cosα, из данной формулы следует cosα= aˉ·bˉ/(|aˉ|·|bˉ|). После подстановки координат векторов и их длин в данную формулу, получается cosα=( x1x2+y1y2)/(√(x12+y12)·√(x22+y22).

Видеоурок «Скалярное произведение в координатах» подробно и понятно разъясняет тему, что позволяет рекомендовать его не только для использования на традиционном уроке в школе, но и для самостоятельного изучения учеником. Также этот материал будет полезен учителю, проводящему дистанционное обучение учеников.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 6541 |
| Номер материала | 758 |