
Урок "Скалярное произведение векторов"

Краткое описание документа:
Видеоурок «Скалярное произведение векторов» раскрывает суть математической операции по скалярному умножению векторов. В ходе урока формулируется понятие скалярного произведения векторов, рассматривается практическое его применение, демонстрируются свойства скалярного произведения, приводится пример приложения данного математического аппарата в курсе физики. Задача видеоурока – облегчить понимание данной темы, способствовать запоминанию учебного материала, формировать умения использовать изученные понятия на практике.

В данном пособии используются разные способы влияния на процессы запоминания. Чтобы удержать внимание учеников на изучении предмета используются анимационные эффекты, голосовое сопровождение. Все рисунки и построения выполняются в цвете, так, чтобы всем ученикам было хорошо видны все преобразования, выделяются важные детали. Комплексное действие всех факторов обучения, используемых в данном уроке, дает возможность заменить видеоматериалом объяснение учителя по данной теме и освободить его для ведения индивидуальной работы с учениками.

Видеоурок начинается с представления темы. Ученикам напоминается, что они уже изучили понятие сложения векторов, а также умножения на число. В ходе данного видеоурока представляется возможность освоить скалярное умножение векторов. Формулируется определение скалярного произведения, получаемого перемножением длин векторов, косинуса, образованного векторами угла. Вводятся обозначения скалярного произведения рассматриваемых векторов aˉ·bˉ или aˉbˉ. Ученикам в виде формулы представлено скалярное произведение векторов aˉ·bˉ= |aˉ|·|bˉ|·cos(aˉ^bˉ).
Рассматриваются частные случаи скалярного произведения. Отмечается, если между векторами aˉ и bˉ угол 90°, то есть они перпендикулярны, так как cos(aˉ^bˉ)=0, их скалярное произведение нулевое. Верно и обратное - при нулевом скалярном произведении величина угла между векторами 90°. На экране демонстрируется доказательство справедливости утверждения. Отмечается, что неравенство нулю векторов означает, что, произведение их длин не равно нулю, а равенство нулю косинуса угла, образованного векторами, означает, что между ними 90°. Вывод о признаке перпендикулярности векторов выведен на экран и выделен цветом для запоминания. Он утверждает, что при ненулевых векторах скалярное произведение будет равно нулю в том случае, когда векторы между собой перпендикулярны.

Следствием из определения является еще одно свойство, которое отмечает положительность или отрицательность значения скалярного произведения. Отмечается, что скалярное произведение является положительным тогда, когда угол между векторами меньше 90°. Скалярное произведение получает отрицательное значение, когда угол между векторами больше 90°. Для наглядной демонстрации свойства производится построение двух векторов aˉ и bˉ, между которыми угол 35°. От начала данных векторов строится еще один вектор сˉ, который составляет с вектором aˉ угол 90°. То есть aˉ^bˉ=35°, а aˉ^сˉ90°, bˉ^сˉ=125°. Это означает, что скалярные произведения построенных векторов будут aˉ·bˉ>0, aˉ·cˉ=0, bˉ·cˉ<0. Если векторы aˉ и bˉ являются сонаправленными, то скалярное произведение получается умножением длин, то есть aˉ·bˉ= |aˉ|·|bˉ|. Скалярное произведение вектора, умноженного на самого себя, будет равно квадрату его длины, иначе aˉ·аˉ=|aˉ|2. Данное произведение иначе называется скалярный квадрат вектора aˉ, обозначение которого, принятое в математике, выводится на экран, а также метод вычисления скалярного квадрата вектора.
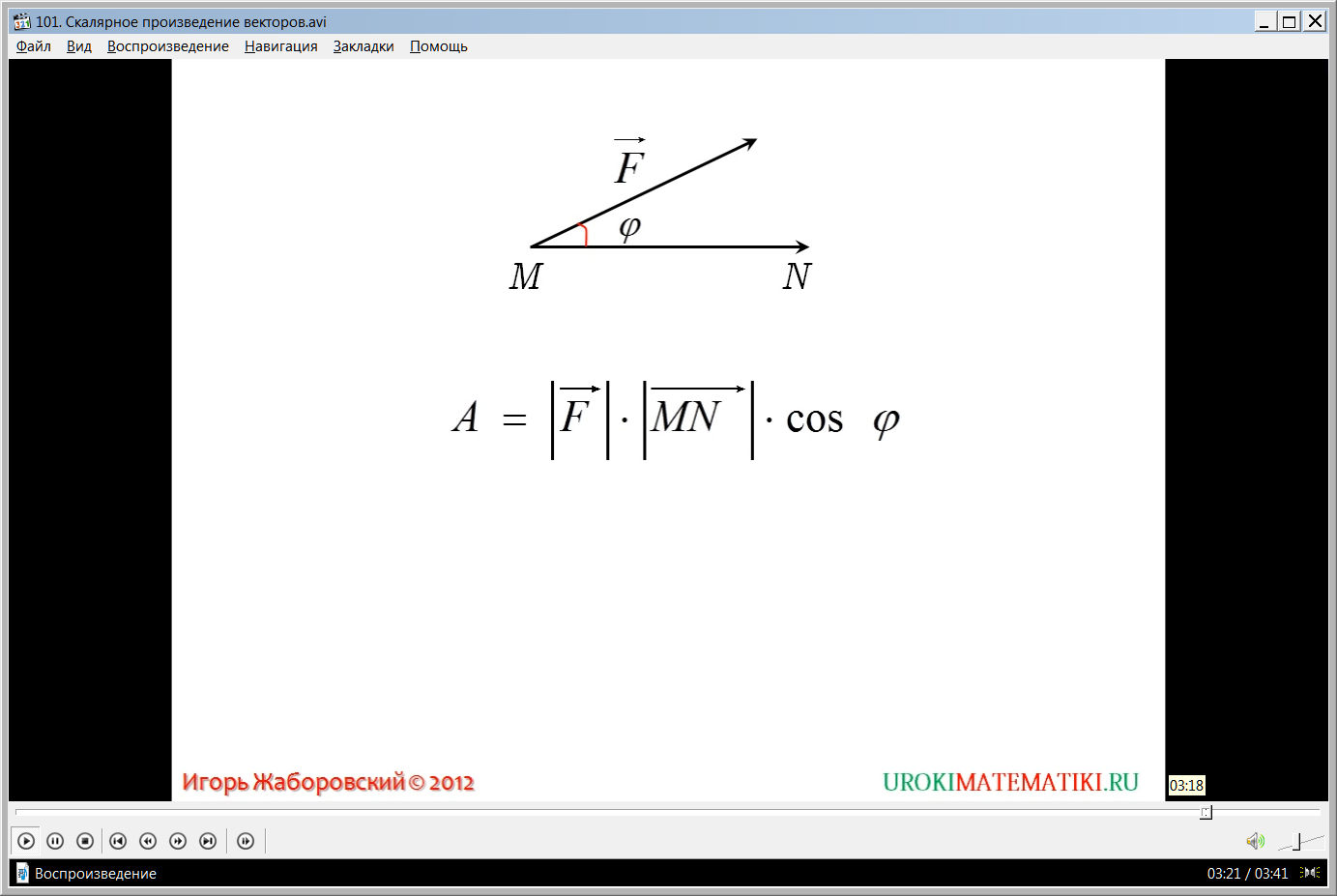
Далее демонстрируется приложение скалярного произведения в курсе физики. Данный математический аппарат помогает найти значение работы некоторой силы, под действием которой производится перемещение тела по направлению из точки Mв N. Демонстрируется построение векторов перемещения и силы, которая направлена под углом φ к направлению движения. Отмечается, что значение работы определяется формулой А=|Fˉ|·MNˉ|·cosφ. Правая часть формулы является скалярным произведением векторов А=Fˉ·MNˉ.
Видеоурок «Скалярное произведение векторов» рекомендуется применять на традиционном уроке математики в качестве наглядного пособия или части урока вместо объяснения. Также данный материал будет полезен ученикам. Желающим самостоятельно освоить или углубить понимание темы. Видеоурок может стать частью урока при дистанционном обучении, потому что подробно и полно раскрывает учебный материал.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 6300 |
| Номер материала | 759 |