
Урок «Сложение и умножение вероятностей»

Краткое описание документа:
Одним из важных моментов при изучении раздела теории вероятностей являются свойства сложения и умножения. Прежде, чем изучать данную тему, необходимо хорошо понимать такие понятия, как: случайная величина, равновозможные исходы, благоприятные исходы, частота, относительная частота и классический метод нахождения вероятности. В противном случае, видеуорок будет непонятен ученику.
Данный материал подойдет для использования в качестве инструмента для интерактивного обучения. Им могут воспользоваться как сами девятиклассники, так и учителя при составлении плана-конспекта, репетиторы.

Учебный материал начинается с рассмотрения некоторого примера, который удачно сопровождается иллюстрациями. Предлагается рассмотреть следующий случай: в ящике имеется определенное количество кубиков трех цветов. Рассматриваются два события, при которых в первом случае кубик красного цвета, во втором – синего. Диктор указывает, что данные события не зависят друг от друга и не влияют никаким образом друг на друга. Одновременно эти события произойти также не могут. Ведь предполагается, что вынимается по одному кубику из ящика. Такие события называются несовместным. На экране можно увидеть это определение. Его можно зафиксировать в тетради.

В таких случаях имеет смысл использовать теорему сложения. Сложение можно использовать в том случае, если предполагаемое событие указывает на то, что произойдет либо первое событие (красный кубик), либо второе (синий кубик). Для того, чтобы найти вероятность такого события, необходимо найти вероятности двух предыдущих событий и сложить их.
Чтобы закрепить данную информацию, рассматривается первая задача. Она имеет интересную и актуальную для девятиклассника формулировку. При решении данной задачи демонстрируется, каким образом необходимо использовать теорему о сложении на практике.
После решения данной задачи и нахождения ответа диктор предлагает рассмотреть свойство вероятностей противоположных событий. Что же такое противоположное событие?
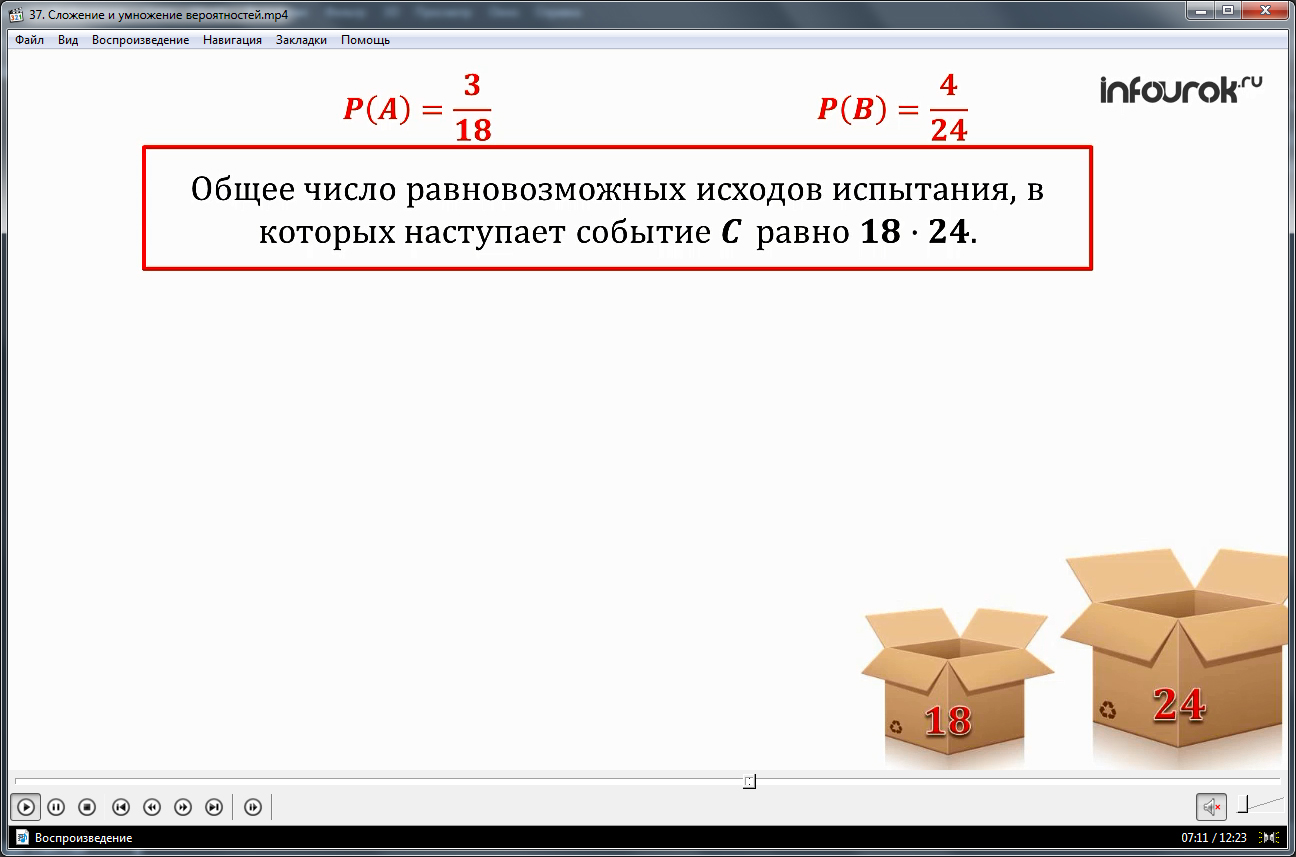
На примере событий при бросании игральной кости приводится ответ на данный вопрос. На иллюстрациях явно можно увидеть два противоположных события Aи B. Легко проверить на практике, что сумма противоположных событий равна 1. Противоположное событие для события А отмечается черточкой сверху, аналогично вектору. Такие события также называются несовместными.
Для закрепления приводится вторая задача. Она пошагово решается и комментируется подробным образом. Далее приводится определение независимого события. Такие события не влияют на вероятности наступления друг друга.
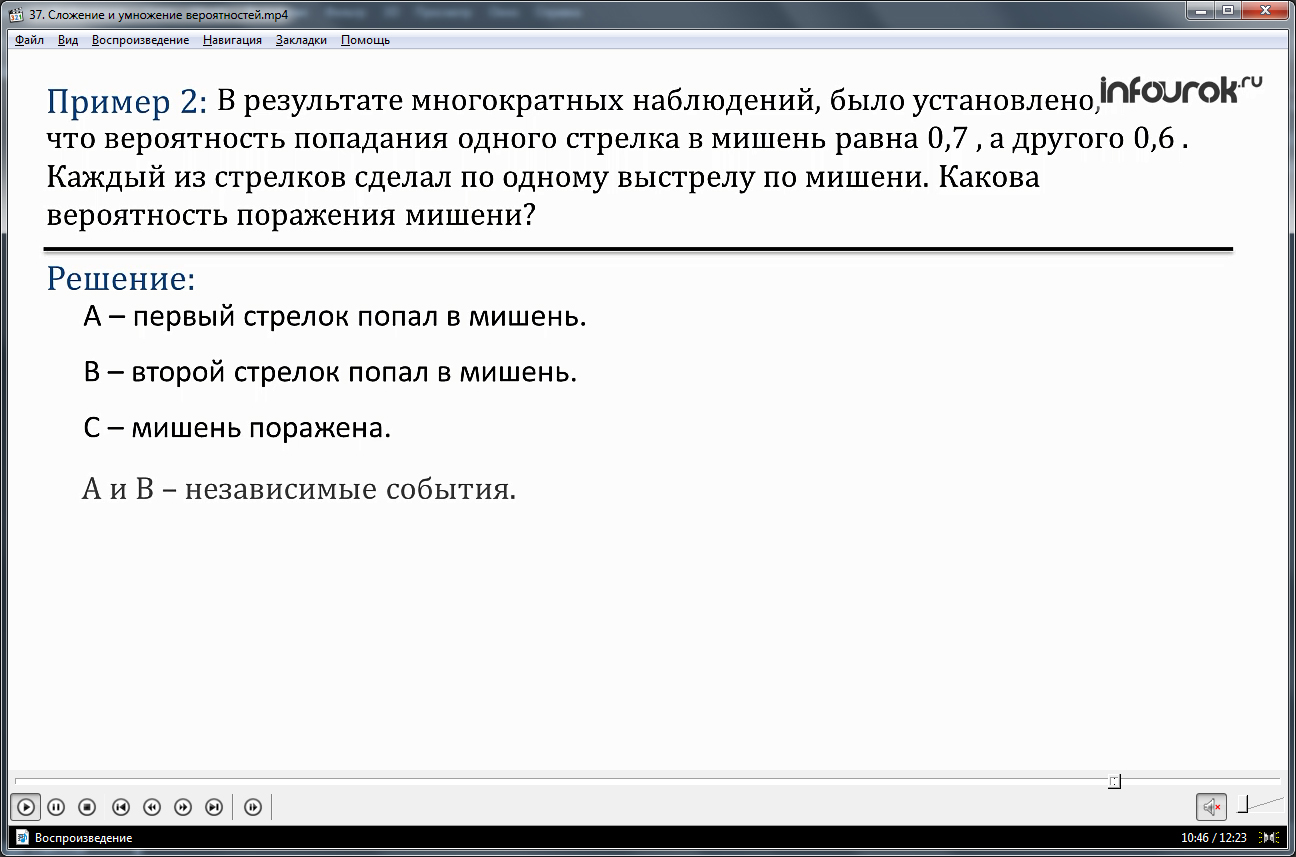
В случае совместных событий имеет смысл рассмотреть свойство сложения вероятностей. Если некоторое событие подразумевает наступления двух других одновременно, то, для того, чтобы найти его вероятность, необходимо перемножить предыдущие 2 события.
Последняя часть видеоурока посвящена решению задач. Для того чтобы максимально хорошо освоить и научиться решать задачи из области теории вероятностей, необходимо решать большое количество задач. В таком случае, школьник сможет быстро и правильно сориентироваться насчет того, какой метод стоит использовать: классический, теорему сложения или умножения?
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 10514 |
| Номер материала | 655 |