
Урок "Статистические характеристики"

Краткое описание документа:
Статистика – одна из древнейших отраслей прикладной математики, которая широко использует теоретическую базу многих арифметических определений для осуществления практической деятельности человека. Ещё в древних государствах возникла необходимость строгого учета дохода граждан по группам, для проведения эффективного процесса налогообложения. Статистические исследования имеют громадное значение для экономического развития общества, и не только. Поэтому, в данном видеоуроке мы рассмотрим основные определения статистических характеристик.
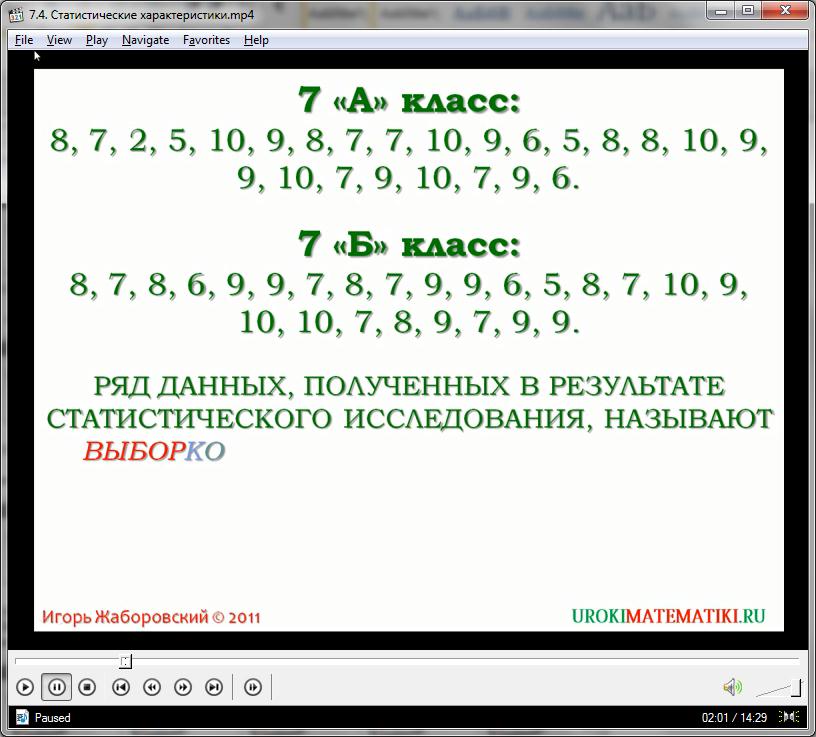
Предположим, нам необходимо изучить статистику выполнения тестов учениками седьмого класса. Для начала нам необходимо создать массив информации, с которым можно работать. Информацией, в данном случае, будут являться цифры, определяющие количество выполненных тестов каждым из учеников. Рассмотрим два класса, содержащие по 15 школьников каждый. Общее задание включало 10 упражнений. Результаты получились следующими:
7А: 4, 10, 6, 4, 7, 8, 2, 10, 8, 5, 7, 9, 10, 6, 3;
7Б: 7, 5, 9, 7, 8, 10, 7, 1, 7, 6, 5, 9, 8, 10, 7.
Мы получили, в математической интерпретации, два множества чисел, состоящие из 15 элементов каждое. Этот информационный массив, сам по себе, мало чем может помочь в оценивании эффективности выполнения заданий. Поэтому его нужно статистически преобразовать. Для этого введем основные понятия статистики. Ряд чисел, полученных в результате исследования, называется выборкой. Каждое число (количество выполненных упражнений) – это варианта выборки. А количество всех чисел (в данном случае, это 30 – сумма всех учеников в обоих классах) является объемом выборки.
Одной из главных статистических характеристик является среднее арифметическое. Это значение определяется как частное, полученное в результате деления суммы значений вариант выборки на её объем. В нашем случае необходимо сложить все полученные значения чисел и поделить их на 15 (если мы вычисляем среднее арифметическое для какого-либо одного класса), либо же на 30 (если мы вычисляем общее среднее арифметическое). В представляемом примере, сумма всех количеств выполненных заданий для класса 7А составит 99. Поделив на 15, получаем 6,6 – это среднее арифметическое выполненных заданий для данной группы учеников.
Работать с хаотичным набором чисел не очень удобно, поэтому очень часто информационный массив приводят к упорядоченному набору данных. Создадим вариационный ряд для 7Б класса, использовав метод постепенного возрастания, располагая числа от меньшего к большему:
1, 5, 5, 6, 7, 7, 7, 7, 7, 8, 8, 9, 9, 10, 10.
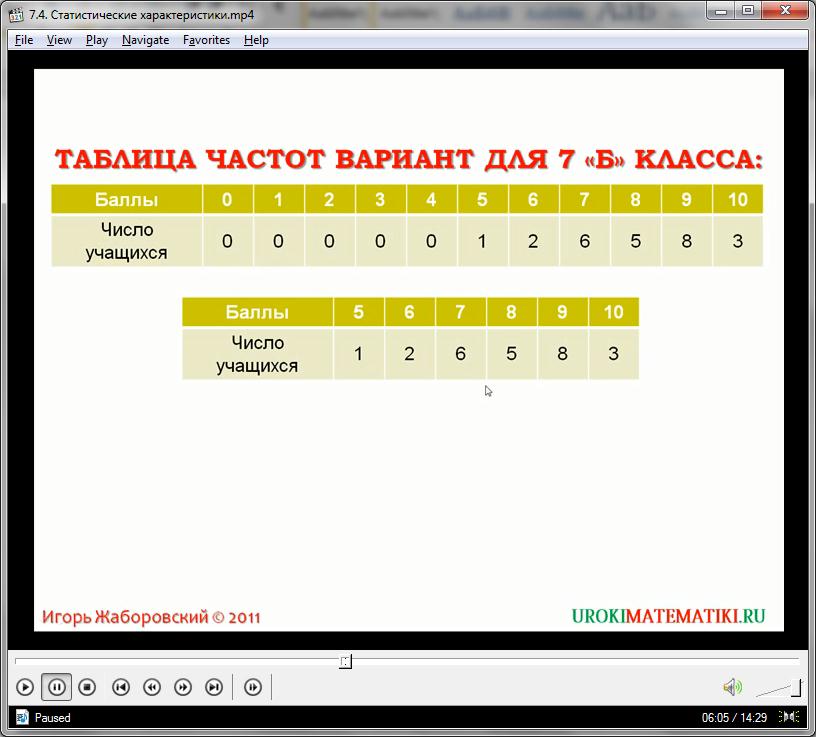
Количество появлений какого-либо одного значения в выборке данных называется частотой варианты выборки. Например, частота варианты «7» в вышеуказанном вариационном ряду легко определяется, и равна она пяти. Для удобства отображения упорядоченный ряд преобразуется в таблицу, отображающую зависимость между стандартным рядом значений вариант, и частотой встречаемости (количеством учеников, выполнивших одинаковое количество задач).

В 7А классе наименьшей вариантой выборки является значение «2», а наибольшей – «10». Интервал между 2 и 10 называется размахом вариационного ряда. Для 7Б класса размах ряда составляет от 1 до 10. Наибольшая, по частоте встречаемости, варианта называется модой выборки – для 7А это число 7, встречающееся 5 раз.
| Автор | |
|---|---|
| Дата добавления | 28.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7897 |
| Номер материала | 443 |