
Урок "Уравнение касательной к графику функции"

Краткое описание документа:
Видеоурок «Уравнение касательной к графику функции» демонстрирует учебный материал для освоения темы. В ходе видеоурока представлен теоретический материал, необходимый для формирования понятия об уравнении касательной к графику функции в данной точке, алгоритм нахождения такой касательной, описаны примеры решения задач с использованием изученного теоретического материала.
В видеоуроке используются методы, улучшающие наглядность материала. В представлении вставлены рисунки, схемы, даются важные голосовые комментарии, применяется анимация, выделение цветом и другими инструментами.
Видеоурок начинается с представления темы урока и изображения касательной к графику некоторой функции y=f(x) в точке M(a;f(a)). Известно, что угловой коэффициент касательной, построенной к графику в данной точке, равен производной функции f΄(a) в данной точке. Также из курса алгебры известно уравнение прямой y=kx+m. Схематично представлено решение задачи нахождения уравнения касательной в точке, которая сводится к нахождению коэффициентов k, m. Зная координаты точки, принадлежащей графику функции, можем найти m, подставив значение координат в уравнение касательной f(a)=ka+m. Из него находим m=f(a)-ka. Таким образом, зная значение производной в данной точке и координаты точки, можно представить уравнение касательной таким образом y=f(a)+f΄(a)(x-a).
Далее рассматривается пример составления уравнения касательной, следуя схеме. Дана функция y=x2, x=-2. Приняв а=-2, находим значение функции в данной точке f(a)= f(-2)=(-2)2=4. Определяем производную функции f΄(х)=2х. В данной точке производная равна f΄(a)= f΄(-2)=2·(-2)=-4. Для составления уравнения найдены все коэффициенты а=-2, f(a)=4, f΄(a)=-4, поэтому уравнение касательной у=4+(-4)(х+2). Упростив уравнение, получаем у=-4-4х.
В следующем примере предлагается составить уравнение касательной в начале координат к графику функции y=tgx. В данной точке а=0, f(0)=0, f΄(х)=1/cos2x, f΄(0)=1. Таким образом, уравнение касательной выглядит у=х.
В качестве обобщения процесс составления уравнения касательной к графику функции в некоторой точке оформляется в виде алгоритма, состоящего из 4 шагов:
- Вводится обозначение а абсциссы точки касания;
- Вычисляется f(a);
- Определяется f΄(х) и вычисляется f΄(a). В формулу уравнения касательной y=f(a)+f΄(a)(x-a) подставляются найденные значения а, f(a), f΄(a).
В примере 1 рассматривается составление уравнения касательной к графику функции у=1/х в точке х=1. Для решения задачи пользуемся алгоритмом. Для данной функции в точке а=1 значение функции f(a)=-1. Производная функции f΄(х)=1/х2. В точке а=1 производная f΄(a)= f΄(1)=1. Используя полученные данные, составляется уравнение касательной у=-1+(х-1), или у=х-2.
В примере 2 необходимо найти уравнение касательной к графику функции у=х3+3х2-2х-2. Основное условие – параллельность касательной и прямой у=-2х+1. Сначала находим угловой коэффициент касательной, равный угловому коэффициенту прямой у=-2х+1. Так как f΄(a)=-2 для данной прямой, то k=-2 и для искомой касательной. Находим производную функции (х3+3х2-2х-2)΄=3х2+6х-2. Зная, что f΄(a)=-2, находим координаты точки 3а2+6а-2=-2. Решив уравнение, получаем а1=0, а2=-2. Используя найденные координаты, можно найти уравнение касательной с помощью известного алгоритма. Находим значение функции в точках f(а1)=-2, f(а2)=-18. Значение производной в точке f΄( а1)= f΄( а2)=-2. Подставив найденные значения в уравнение касательной, получим для первой точки а1=0 у=-2х-2, а для второй точки а2=-2 уравнение касательной у=-2х-22.
В примере 3 описывается составление уравнения касательной для ее проведения в точке (0;3) к графику функции y=√x. Решение производится по известному алгоритму. Точка касания имеет координаты х=а, где а>0. Значение функции в точке f(a)=√x. Производная функции f΄(х)=1/2√х, поэтому в данной точке f΄(а)=1/2√а. Подставив все полученные значения в уравнение касательной, получаем у=√а+(х-а)/2√а. Преобразовав уравнение, получаем у=х/2√а+√а/2. Зная, что касательная проходит через точку (0;3), находим значение а. Находим а из 3=√а/2. Отсюда √а=6, а=36. Находим уравнение касательной у=х/12+3. На рисунке изображается график рассматриваемой функции и построенная искомая касательная.
Ученикам напоминаются приближенные равенства Δy=≈f΄(x)Δxи f(x+Δx)-f(x)≈f΄(x)Δx. Принимая х=а, x+Δx=х, Δx=х-а, получаем f(х)- f(а)≈f΄(а)(х-а), отсюда f(х)≈f(а)+f΄(а)(х-а).
В примере 4 необходимо найти приближенное значение выражение 2,0036. Так как необходимо отыскать значение функции f(х)=х6 в точке х=2,003, можем воспользоваться известной формулой, приняв f(х)=х6, а=2, f(а)= f(2)=64, f΄(x)=6х5. Производная в точке f΄(2)=192. Поэтому 2,0036≈65-192·0,003. Вычислив выражение, получаем 2,0036≈64,576.
Видеоурок «Уравнение касательной к графику функции» рекомендуется использовать на традиционном уроке математики в школе. Учителю, осуществляющему обучению дистанционно, видеоматериал поможет более понятно объяснить тему. Видео может быть рекомендовано для самостоятельного рассмотрения учениками при необходимости углубить их понимание предмета.
ТЕКСТОВАЯ РАСШИФРОВКА:
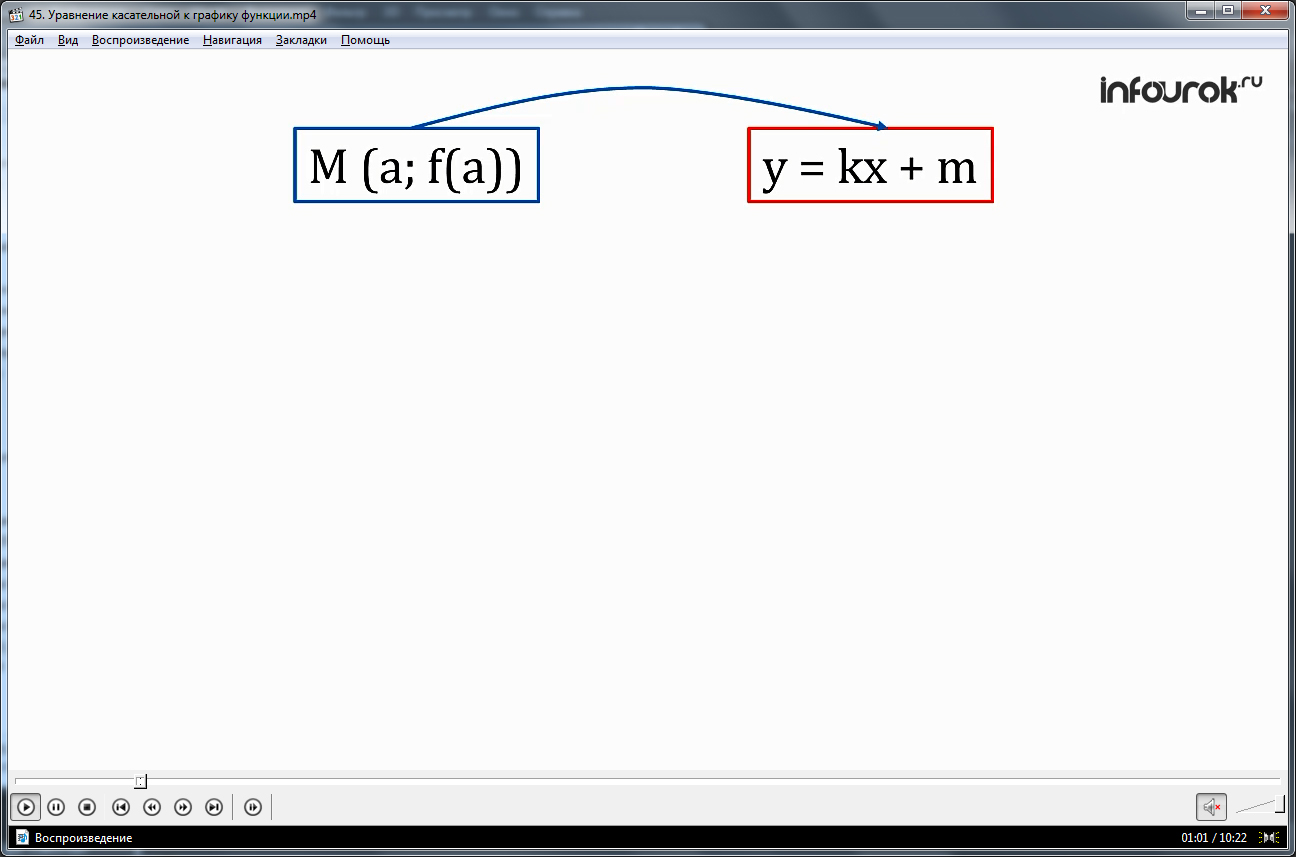
Нам известно, что если точка М (а; f(а)) (эм с координатами а и эф от а) принадлежит графику функции у =f (x) и если в этой точке к графику функции можно провести касательную, не перпендикулярную к оси абсцисс, то угловой коэффициент касательной равен f'(a) (эф штрих от а).
Пусть даны функция у = f(x) и точка М (a; f(a)), a также известно, что существует f´(a). Составим уравнение касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат, имеет вид y = kx+m (игрек равный ка икс плюс эм), поэтому задача состоит в отыскании значений коэффициентов k и m.(ка и эм)
Угловой коэффициент k= f'(a). Для вычисления значения m воспользуемся тем, что искомая прямая проходит через точку М(а; f (а)). Это значит, что, если подставить координаты точки М в уравнение прямой, получим верное равенство: f(a) = ka+m, откуда находим, что m = f(a) – ka.
Осталось подставить найденные значения коэффициентов kи mв уравнение прямой:
y = kx+m;
y = kx+(f(a) –ka);
y = f(a)+k(x–a);
y=f(a)+f'(a) (x–a). (игрек равен эф от а плюс эф штрих от а, умноженный на икс минус а).

Нами получено уравнение касательной к графику функции y = f(x) в точке х=а.
Если, скажем, у = х2 и х= –2 (т.е. а = –2), то f(а) = f(–2) = (–2)2 =4; f´(x) = 2х, значит, f'(a) = f´(–2) = 2·(–2) = –4. ( то эф от а равно четыре, эф штрих от икс равно два икс, значит эф штрих от а равно минус четыре)
Подставив в уравнение найденные значения a = –2, f(a) = 4, f'(a) = –4, получим: у = 4+(–4)(х+2), т.е. у = –4х–4.
(игрек равен минус четыре икс минус четыре)
Составим уравнение касательной к графику функции у = tgx(игрек равен тангенс икс) в начале координат. Имеем: а = 0, f(0) = tg0=0;
f'(x)= , значит, f'(0) = l. Подставив в уравнение найденные значения а=0, f(a)=0, f´(a) = 1, получим: у=х.
Обобщим наши шаги нахождения уравнения касательной к графику функции в точке х с помощью алгоритма.
АЛГОРИТМ СОСТАВЛЕНИЯ УРАВНЕНИЯ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ у = f(x):
1) Обозначить абсциссу точки касания буквой а.
2) Вычислить f (а).
3) Найти f´(x) и вычислить f´(a).
4) Подставить найденные числа a, f(a), f´(а) в формулуy=f(a)+f'(a) (x–a).
Пример 1. Составить уравнение касательной к графику функции у = – в
точке х = 1.
Решение. Воспользуемся алгоритмом, учитывая, что в данном примере
f(x) = –.
1) a=1.
2) f(a)=f(1)=– =–1
3) f´(x)=; f´(a)= f´(1)= =1.
4) Подставим найденные три числа: а = 1, f(а) = –1, f'(а) = 1 в формулу. Получим: у = –1+(х–1), у = х–2.
Ответ: у = х–2.
Пример 2. Дана функция у = х3+3х2–2х–2. Записать уравнение касательной к графику функции у= f(х), параллельной прямой у = –2х +1.
Решение.
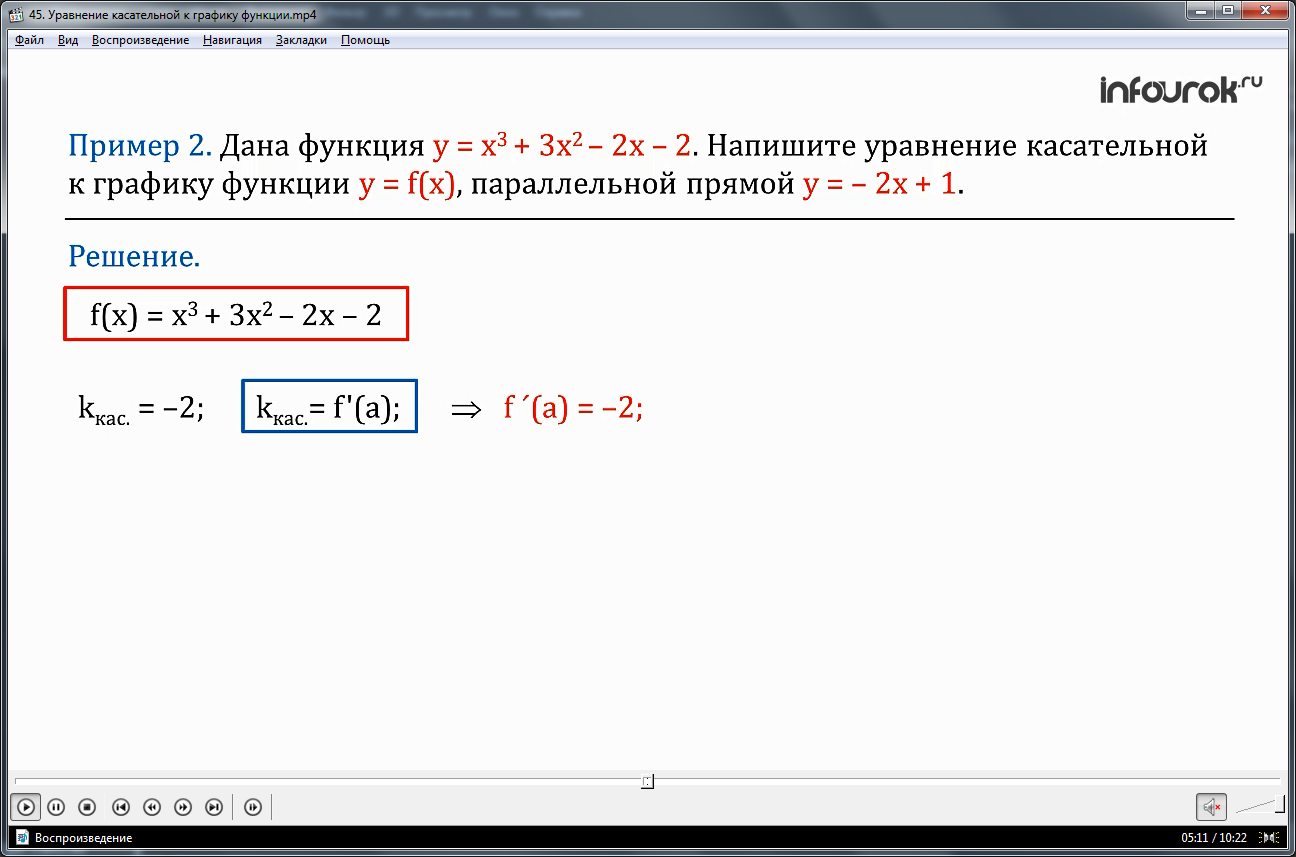
Используя алгоритм составления уравнения касательной, учтем, что в данном примере f(x) = х3+3х2–2х–2, но здесь не указана абсцисса точки касания.
Начнем рассуждать так. Искомая касательная должна быть параллельна прямой у = –2х+1. А параллельные прямые имеют равные угловые коэффициенты. Значит, угловой коэффициент касательной равен угловому коэффициенту заданной прямой: kкас. = –2. Hokкас.= f'(a). Таким образом, значение а мы можем найти из уравнения f ´(а) = –2.
Найдем производную функции у=f(x):
f'(x)= (х3+3х2–2х–2)´ =3х2+6х–2; f'(а)= 3а2+6а–2.
Из уравнения f'(а) = –2, т.е. 3а2+6а–2 =–2 находим а1 =0, a2 =–2. Значит, имеются две касательные, удовлетворяющие условию задачи: одна в точке с абсциссой 0, другая в точке с абсциссой –2.
Теперь можно действовать по алгоритму.
1) а1=0, а2=–2.
2) f(a1)= 03+3·02–2∙0–2=–2; f(a2)=(–2)3+3·(–2)2–2·(–2)–2=6;
3) f'(a1) = f'(a2) = –2.
4) Подставив значения a1= 0, f(a1) =–2, f'(a1) = –2 в формулу, получим:
у=–2–2(х–0), у=–2х–2.
Подставив значения а2=–2, f(a2) =6, f'(a2)= –2 в формулу, получим:
у=6–2(х+2), у=–2х+2.
Ответ: у=–2х–2, у=–2х+2.
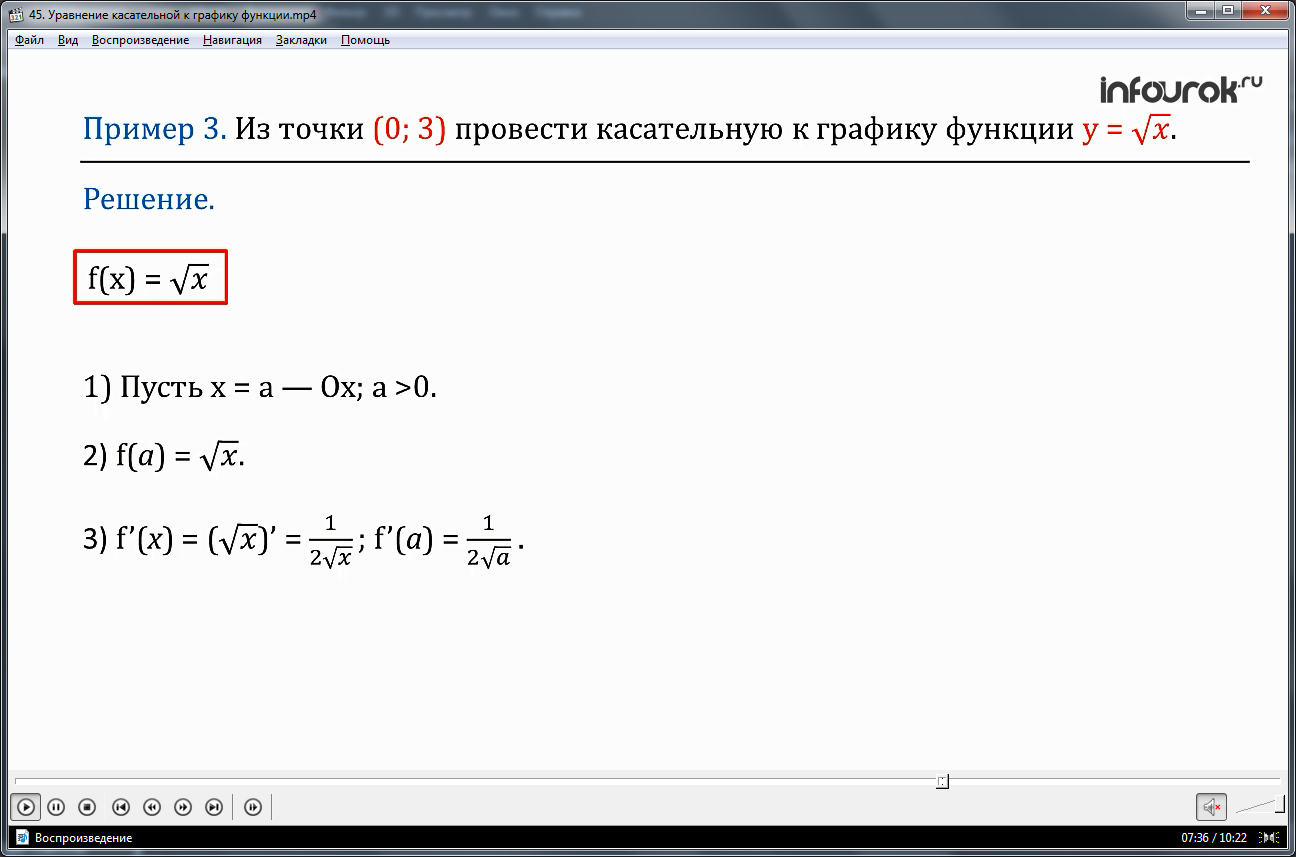
Пример 3. Из точки (0; 3) провести касательную к графику функции у = . Решение. Воспользуемся алгоритмом составления уравнения касательной, учитывая, что в данном примере f(x) = . Заметим, что и здесь, как в примере 2, не указана явно абсцисса точки касания. Тем не менее, действуем по алгоритму.
1) Пусть х = а — абсцисса точки касания; ясно, что а >0.
2) f(a)=.
3) f´(x)=()´=; f´(a) =.
4) Подставив значения a, f(a) = , f'(a) = в формулу
y=f (a) +f '(a) (x–a), получим:
y=+(x-a);
y=+.
По условию касательная проходит через точку (0; 3). Подставив в уравнение значения х = 0, у = 3, получим: 3 = , и далее =6, a =36.
Как видите, в этом примере только на четвертом шаге алгоритма нам удалось найти абсциссу точки касания. Подставив значение a =36 в уравнение, получим: y=+3
Рис 1
На рис. 1 представлена геометрическая иллюстрация рассмотренного примера: построен график функции у =, проведена прямая у = +3.
Ответ: у = +3.
Нам известно, что для функции y = f(x), имеющей производную в точке х, справедливо приближенное равенство: Δyf´(x)Δx (дельта игрек приближенно равно эф штрих от икс, умноженное на дельта икс)
или, подробнее, f(x+Δx)–f(x) f´(x) Δx (эф от икс плюс дельта икс минус эф от икс приближенно равно эф штрих от икс на дельта икс).
Для удобства дальнейших рассуждений изменим обозначения:
вместо х будем писать а,
вместо х+Δxбудем писать х
вместо Δх будем писать х–а.
Тогда написанное выше приближенное равенство примет вид:
f(x)–f(a)f´(a)(x–a)
или
f(x)f(a)+f´(a)(x–a). (эф от икс приближенно равно эф от а плюс эф штрих от а, умноженное на разность икса и а ).
Пример 4. Найти приближенное значение числового выражения 2,0036.
Решение. Речь идет об отыскании значения функции у = х6 в точке х = 2,003. Воспользуемся формулой f(x)f(a)+f´(a)(x–a), учтя, что в данном примере f(x)=x6, a = 2,f(a) = f(2) = 26=64; x = 2,003, f'(x) = 6x5 и, следовательно, f'(а) = f'(2) = 6·25=192.
В итоге получаем:
2,0036 64+192· 0,003, т.е. 2,0036=64,576.
Если мы воспользуемся калькулятором, то получим:
2,0036= 64,5781643...
Как видите, точность приближения вполне приемлема.
Ответ: 2,0036 =64,576.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 10945 |
| Номер материала | 868 |