
Урок "Сложение и вычитание алгебраических дробей с разными знаменателями"

Краткое описание документа:
Видеоурок «Сложение и вычитание алгебраических дробей с разными знаменателями» является наглядным пособием, с помощью которого дается теоретический материал, подробно объясняются алгоритмы и особенности выполнения операций вычитания, сложения дробей, имеющих различные знаменатели. С помощью пособия учителю легче сформировать умение учеников выполнять операции с алгебраическими дробями. В ходе видеоурока рассматривается ряд примеров, решение которых описывается подробно, обращая внимание на важные детали.
Применение видеоурока на уроке математики дает возможность учителю быстрее достичь учебных целей, повысить эффективность обучения. Наглядность демонстрации помогает ученикам запомнить материал, более глубоко его освоить, поэтому видео может использоваться, сопровождая объяснение учителя. Если же данное видео используется как часть урока, то освобождается время учителя для усиления индивидуальной работы и использования других инструментов обучения для повышения эффективности обучения.
Демонстрация начинается с представления темы видеоурока. Отмечается, что выполнение операций вычитания, сложения алгебраических дробей аналогично выполнению операций с обыкновенными дробями. Напоминается механизм вычитания, сложения для обыкновенных дробей – приводятся дроби к общему знаменателю, после выполняются непосредственно сами операции.
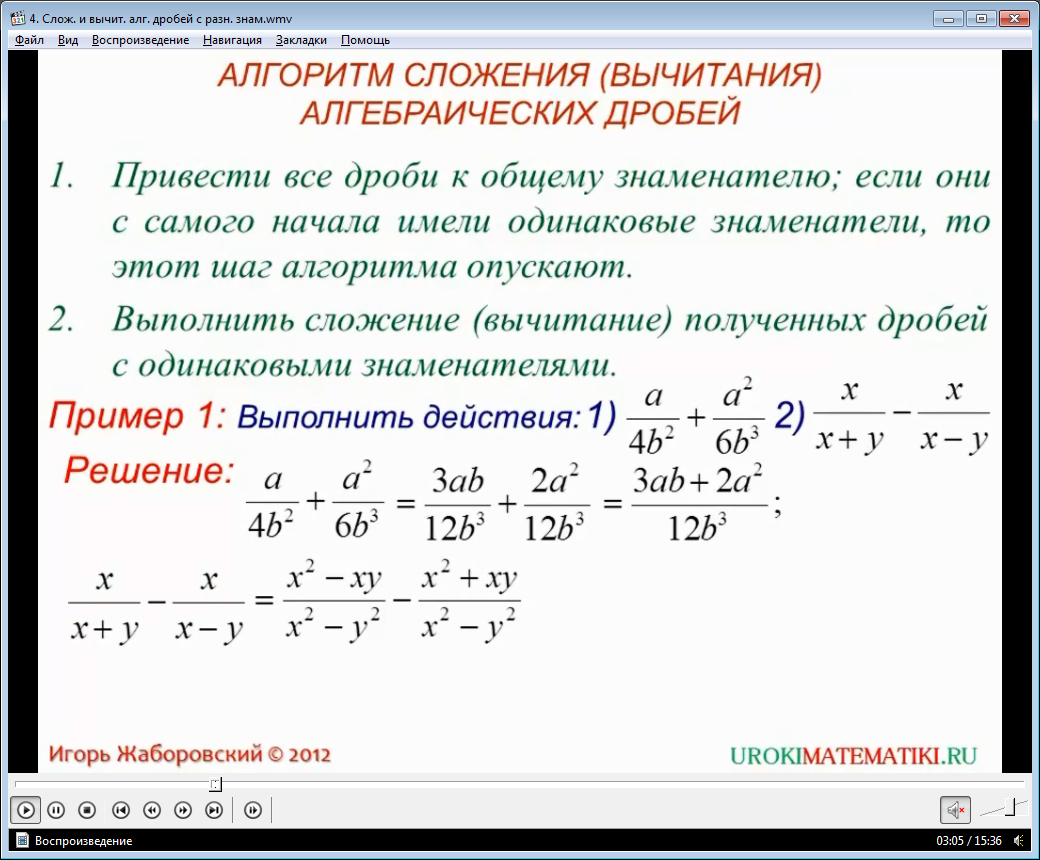
Озвучивается и описывается на экране алгоритм вычитания, сложения алгебраических дробей. Он состоит из двух шагов – приведение дробей к одинаковым знаменателям и затем выполнение сложения (или вычитания) дробей с равными знаменателями. Применение алгоритма рассматривается на примере нахождения значений выражений a/4b2-a2/6b3 , а также x/(х+у)-x/(х-у). Отмечается, что для решения первого примера необходимо привести обе дроби к одному знаменателю. Этим знаменателем будет 12b3. Приведение данных дробей к знаменателю 12b3 подробно рассматривалось в прошлом видеоуроке. В результате преобразования получается две дроби с равными знаменателями 3ab/12b3 и 2a2/12b3. Эти дроби складываются согласно правилу сложения дробей с равными знаменателями. После сложения числителей дробей в результате получается дробь (3ab+2a2)/12b3. Далее описывается решение примера х/(x+у)-x/(х-у). После приведения дробей к одному знаменателю получаются дроби (х2-ху)/( х2-у2) и (х2+ху)/( х2-у2). Согласно правилу вычитания дробей с равными знаменателями, производим операцию с числителями, после чего получается дробь -2ху/(х2-у2).
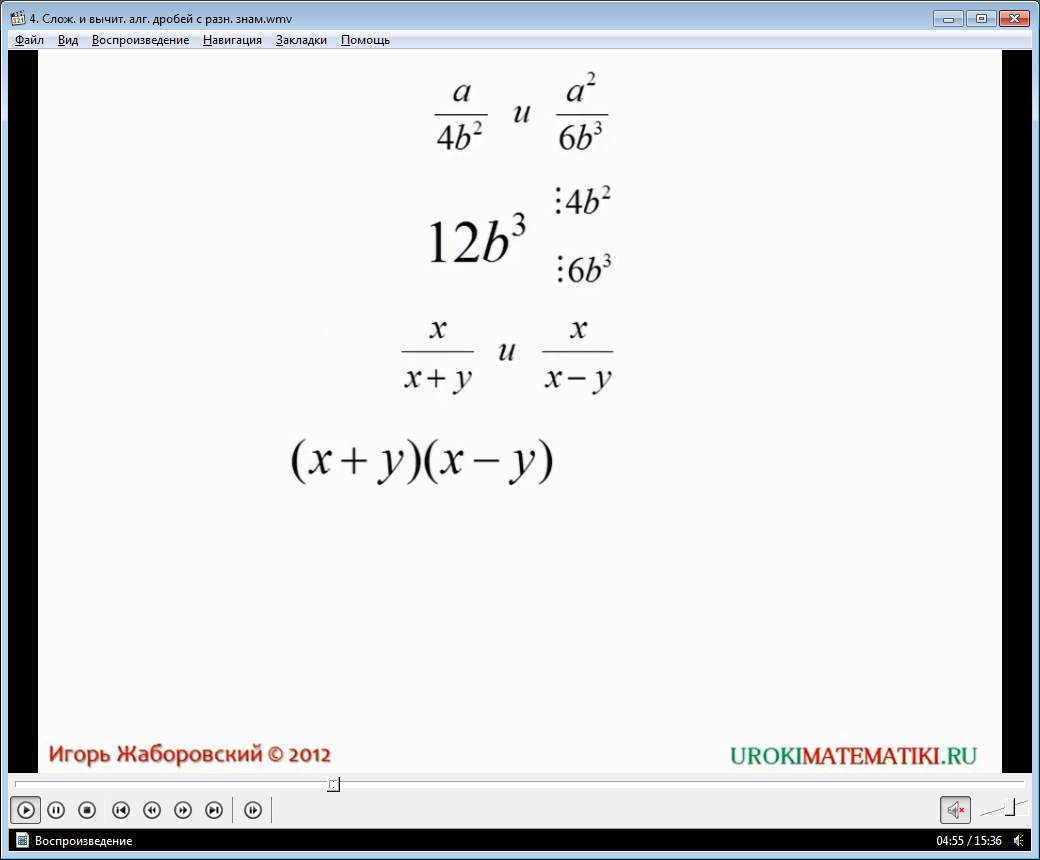
Отмечается, что самым трудным шагом в решении задач на сложение, вычитание дробей, имеющих различные знаменатели, является приведение их к общему знаменателю. Делаются подсказки, как легче выработать навыки в решении этих задач. Разбирается общий знаменатель дроби. Он состоит из числового коэффициента с переменной, возведенной в степень. Видно, что выражение может делиться на знаменатели первой и второй дробей. При этом числовой коэффициент 12 является наименьшим общим кратным числовых коэффициентов дробей 4 и 6. А переменную b содержат оба знаменателя 4b2 и 6b3. При этом в общем знаменателе содержится переменная в наибольшей степени среди знаменателей исходных дробей. Также рассматривается нахождение общего знаменателя для х/(x+у) и x/(х-у). Отмечается, что общий знаменатель (x+у)(x-у) делится на каждый знаменатель. Итак, решение задачи сводится к нахождению наименьшего общего кратного имеющихся числовых коэффициентов, а также нахождению высшего показателя степени для буквенной переменной, встречающейся несколько раз. Затем после сбора данных частей в общее произведение получается общий знаменатель.
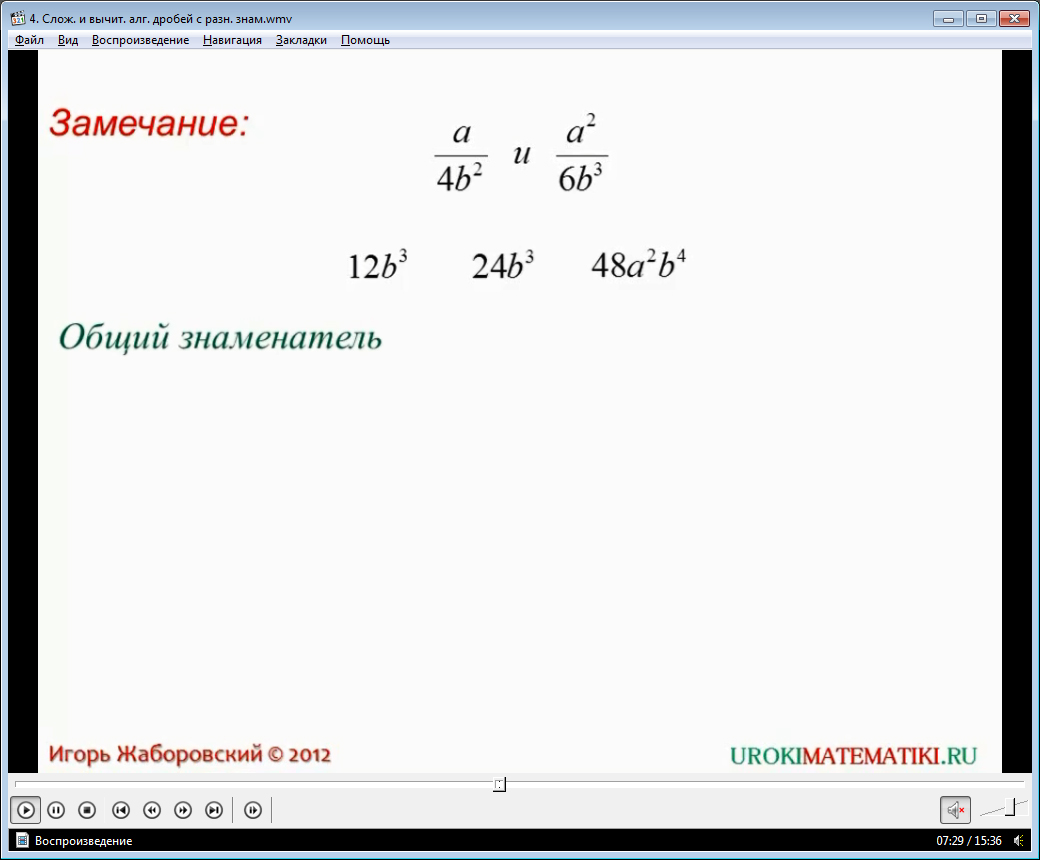
Озвучивается и формулируется на экране алгоритм нахождения для нескольких дробей общего знаменателя. Этот алгоритм состоит из четырех этапов, в первом из которых знаменатели раскладываются на множители. На втором этапе алгоритма отыскивается наименьшее общее кратное имеющихся данных коэффициентов, входящих в состав знаменателей дробей. На третьем этапе составляется произведение, в состав которого входят буквенные множители разложений знаменателей, при этом буквенный показатель, присутствующий в нескольких знаменателях, выбирается в наибольшей степени. На четвертом этапе числовые и буквенные множители, найденные на предыдущих этапах, собираются в одно произведение. Это и будет общий знаменатель. К рассмотренному алгоритму делается замечание. В примере нахождения общего знаменателя дробей a/4b2 и a2/6b3 отмечается, что кроме 12b3 есть и другие знаменатели 24b3 и 48a2b3. И для каждого множества дробей можно найти много общих знаменателей. Однако знаменатель 12b3 является наиболее простым и удобным, поэтому его называют также наименьшим общим знаменателем исходных дробей. Дополнительные множители представляют собой результат частного общего знаменателя и исходного знаменателя дроби. Подробно демонстрируется с помощью анимации, как числитель, знаменатель дробей умножается на дополнительный множитель.
Дальше предлагается рассмотреть алгоритм приведения к общему знаменателю алгебраических дробей в более простой форме, чтобы он был более понятным для учеников. Он также состоит из четырех этапов, в первом из которых разложение знаменателей на множители. Затем предлагается из первого знаменателя выписать все множители, из остальных знаменателей произведение дополнить недостающими множителями. Таким образом находится общий знаменатель. Находятся дополнительные множители к каждой дроби из тех множителей знаменателя, что не попали в общий знаменатель. Четвертым шагом является определение для каждой дроби нового числителя, являющегося произведением старого числителя и дополнительного множителя. Потом каждая дробь записывается с новым числителем и знаменателем.
В следующем примере описывается упрощение выражения 3а/(4а2-1)-(а+1)/(2а2+а). На первом этапе решения знаменатели каждой дроби раскладывается на множители. Для произведений общим множителем является (2а+1). Дополнив произведение оставшимися множителями (2а-1) и а, получается общий знаменатель вида а(2а-1)(2а+1). Строится вспомогательная таблица, в которой указываются общий знаменатель, знаменатели, дополнительные множители. На втором этапе решения каждый числитель умножается на дополнительный множитель, выполняется вычитание. В результате получается дробь (а2-а+1)/а(2а-1)(2а+1).

В примере 3 рассматривается упрощение выражения b/(2a4+4a3b+2a2b2)-1/(3ab2-3a3)+b/(6a4-6a3b). Решение также разбирается по этапам, обращается внимание на существенные особенности выполнения операций, подробно описывается приведение дробей к общему знаменателю, выполнение операций с числителем. В результате вычислений и после преобразования получается дробь (2а3+6а2b-ab2+b3)/6a3(a-b)(a+b)2.
Видеоурок «Сложение и вычитание алгебраических дробей с разными знаменателями» может послужить средством повышения эффективности урока математики по данной теме. Пособие пригодится учителю, осуществляющему дистанционное обучение, для наглядного представления учебного материала. Ученикам видеоурок может быть рекомендованным для самостоятельного обучения, так как в нем подробно и понятно объясняются особенности выполнения изучаемых операций.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6031 |
| Номер материала | 528 |