
Урок "Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень"

Краткое описание документа:
Видеоурок «Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень» - вспомогательное средство для ведения урока математики по данной теме. С помощью видеоурока учителю легче сформировать у учеников умение выполнять умножение и деление алгебраических дробей. Наглядное пособие содержит подробное понятное описание примеров, в которых выполняются операции умножения и деления. Материал может быть продемонстрирован во время объяснения учителя или стать отдельной частью урока.
Чтобы сформировать умение решать задания на умножение и деление алгебраических дробей, по ходу описания решения даются важные комментарии, моменты, требующие запоминания и глубокого понимания выделяются с помощью цвета, жирного шрифта, указателей. С помощью видеоурока учитель может повысить эффективность урока. Данное наглядное пособие поможет быстро и эффективно достичь учебных целей.
Видеоурок начинается с представления темы. После этого указывается, что операции умножения и деления с алгебраическими дробями производятся аналогично операциям с обыкновенными дробями. На экране демонстрируются правила умножения, деления и возведения в степень дробей. С помощью буквенных параметров демонстрируется умножение дробей. Отмечается, что при умножении дробей числители, а также знаменатели перемножаются. Так получается результирующая дробь a/b·c/d=ac/bd. Демонстрируется деление дробей на примере выражения a/b:c/d. Указывается, что для выполнения операции деления необходимо в числитель записать произведение числителя делимого и знаменателя делителя. Знаменателем частного становится произведение знаменателя делимого и числителя делителя. Таким образом, операция деления превращается в операцию умножения дроби делимого и дроби, обратной делителю. Возведение в степень дроби приравнивается дроби, в которой числитель и знаменатель возводятся в назначенную степень.
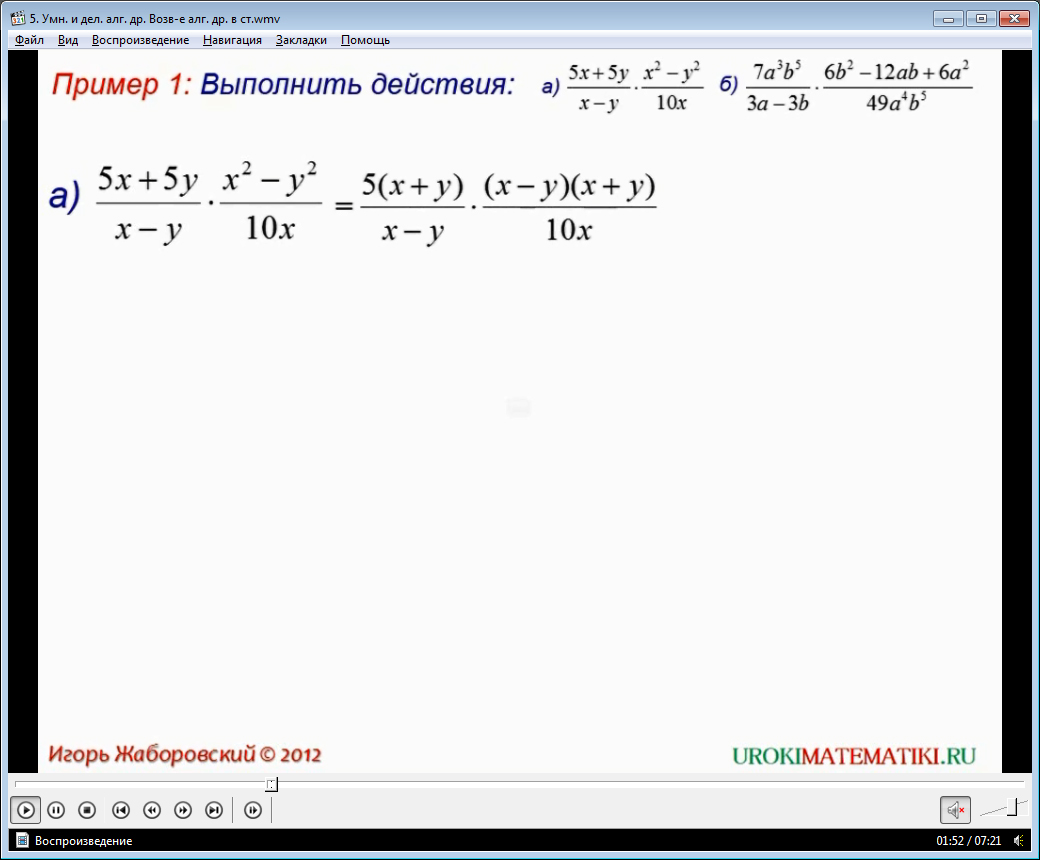
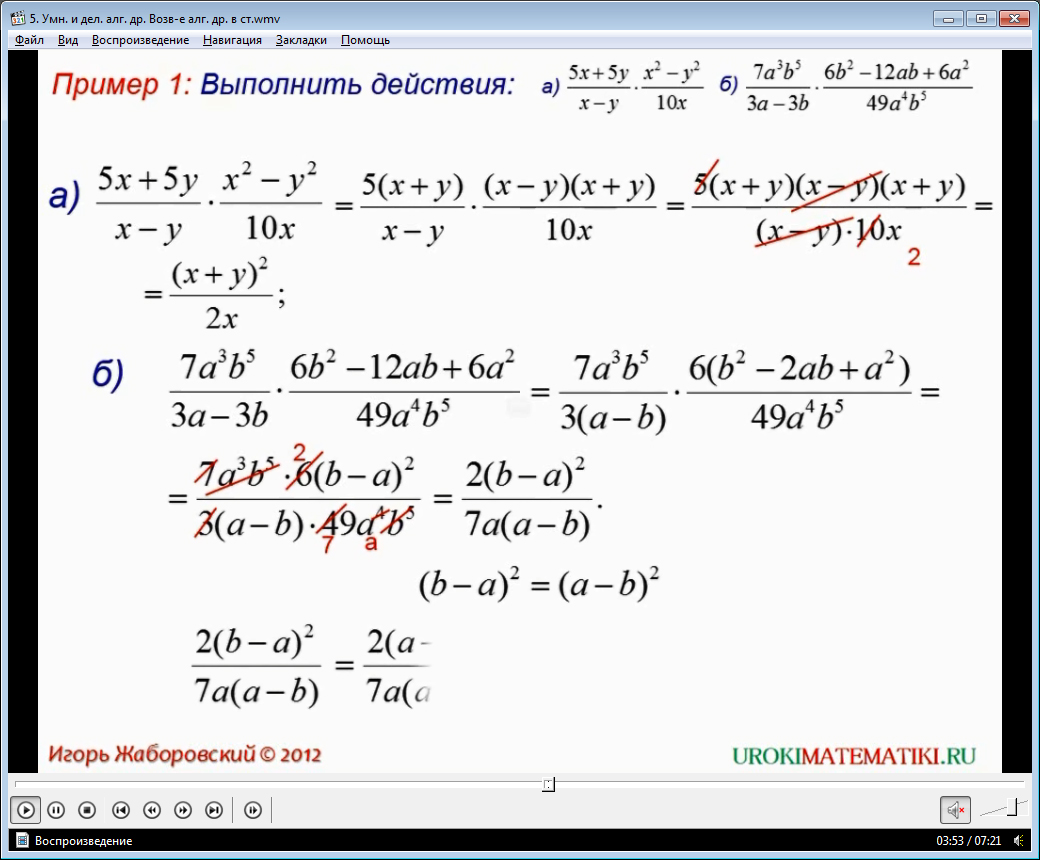
Далее рассматривается решение примеров. В примере 1 необходимо выполнить действия (5х-5у)/(х-у)·(х2-у2)/10х. Чтобы решить данный пример, числитель второй дроби, входящей в произведение, раскладывается на множители. Используя формулы сокращенного умножения, делается преобразование х2-у2=(х+у)(х-у). Затем числители дробей и знаменатели перемножаются. После проведения операций видно, что в числителе и знаменателе есть множители, которые можно сократить, используя основное свойство дроби. В результате преобразований получается дробь (х+у)2/2х. Здесь же рассматривается выполнение действий 7а3b5/(3a-3b)·(6b2-12ab+6a2)/49a4b5. Все числители и знаменатели рассматриваются на предмет возможности разложения на множители, выделения общих множителей. Затем перемножаются числители и знаменатели. После умножения производятся сокращения. Результатом преобразования становится дробь 2(a-b)/7а.
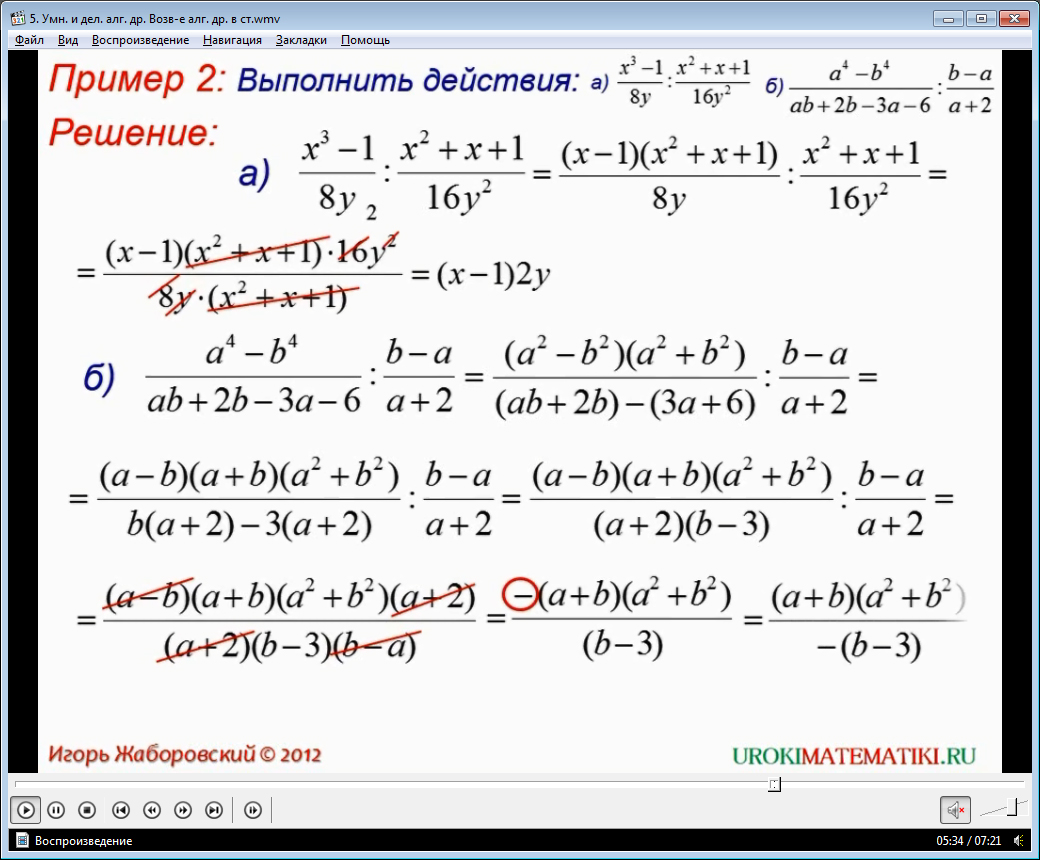
Рассматривается пример, в котором необходимо выполнить действия (х3-1)/8у:(х2+х+1)/16у2. Чтобы решить выражение, предлагается преобразовать числитель первой дроби, используя формулу сокращенного умножения х3-1=(х-1)(х2+х+1). Согласно правилу деления дробей, первая дробь умножается на дробь, обратную второй. После перемножения числителей и знаменателей получается дробь, которая содержит в числителе и знаменателе одинаковые множители. Они сокращаются. В результате получается дробь (х-1)2у. Здесь же описывается решение примера (a4-b4)/(ab+2b-3a-6):(b-a)(a+2). Аналогично предыдущему примеру, для преобразования числителя применяется формула сокращенного умножения. Также преобразуется знаменатель дроби. Затем первая дробь перемножается с дробью, обратной второй дроби. После умножения выполняются преобразования, сокращения числителя и знаменателя на общие множители. В результате получается дробь –(a+b)(a2+b2)/(b-3). Обращается внимание учеников, как меняются знаки числителя и знаменателя при умножении.
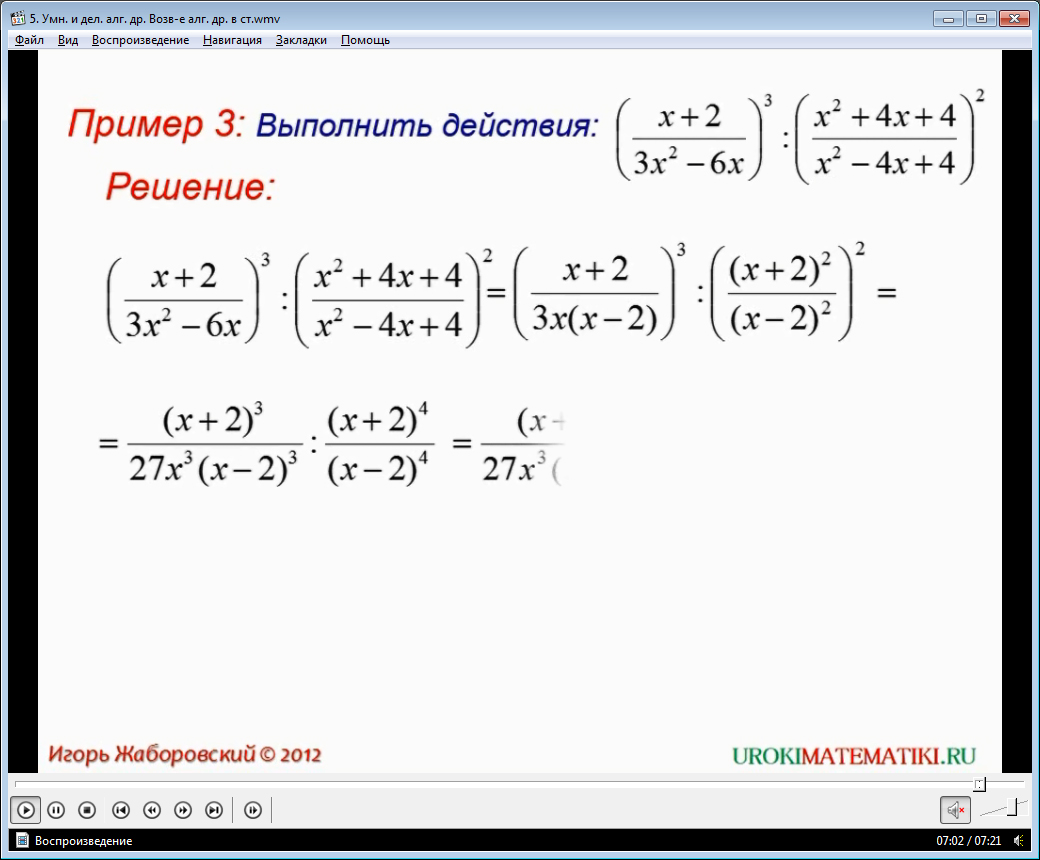
В третьем примере необходимо выполнить действия с дробями ((х+2)/(3х2-6х))3:((х2+4х+4)/(х2-4х+4))2. В решении данного примера применяется правило возведения дроби в степень. И первая, и вторая дробь возведены в степень. Они преобразуются возведением в степень числители и знаменателя дроби. Кроме того, для преобразования знаменателей дробей применяется формула сокращенного умножения, выделение общего множителя. Чтобы поделить первую дробь на вторую, необходимо умножить первую дробь на обратную дробь ко второй. В числителе и знаменателе образуются выражения, которые можно сократить. После преобразования получается дробь (х-2)/27х3(х+2).
Видеоурок «Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень» применяется для повышения эффективности традиционного урока математики. Материал может быть полезен учителю, осуществляющему обучение дистанционно. Детальное понятное описание решения примеров поможет ученикам, самостоятельно осваивающим предмет или требующим дополнительных занятий.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8002 |
| Номер материала | 529 |