
Урок «Степень с рациональным показателем»

Краткое описание документа:
Видеоурок «Степень с рациональным показателем» содержит наглядный учебный материал для ведения урока по данной теме. В видеоуроке содержится информация о понятии степени с рациональным показателем, свойства, таких степеней, а также примеры, описывающие применение учебного материала для решения практических задач. Задача данного видеоурока – наглядно и понятно представить учебный материал, облегчить его освоение и запоминание учениками, формировать умение решать задачи с использованием изученных понятий.
Основные преимущества видеоурока – возможность производить наглядно преобразования и вычисления, возможность использования анимационных эффектов для улучшения эффективности обучения. Голосовое сопровождение помогает развивать правильную математическую речь, а также дает возможность заменить объяснение учителя, освобождая его для проведения индивидуальной работы.
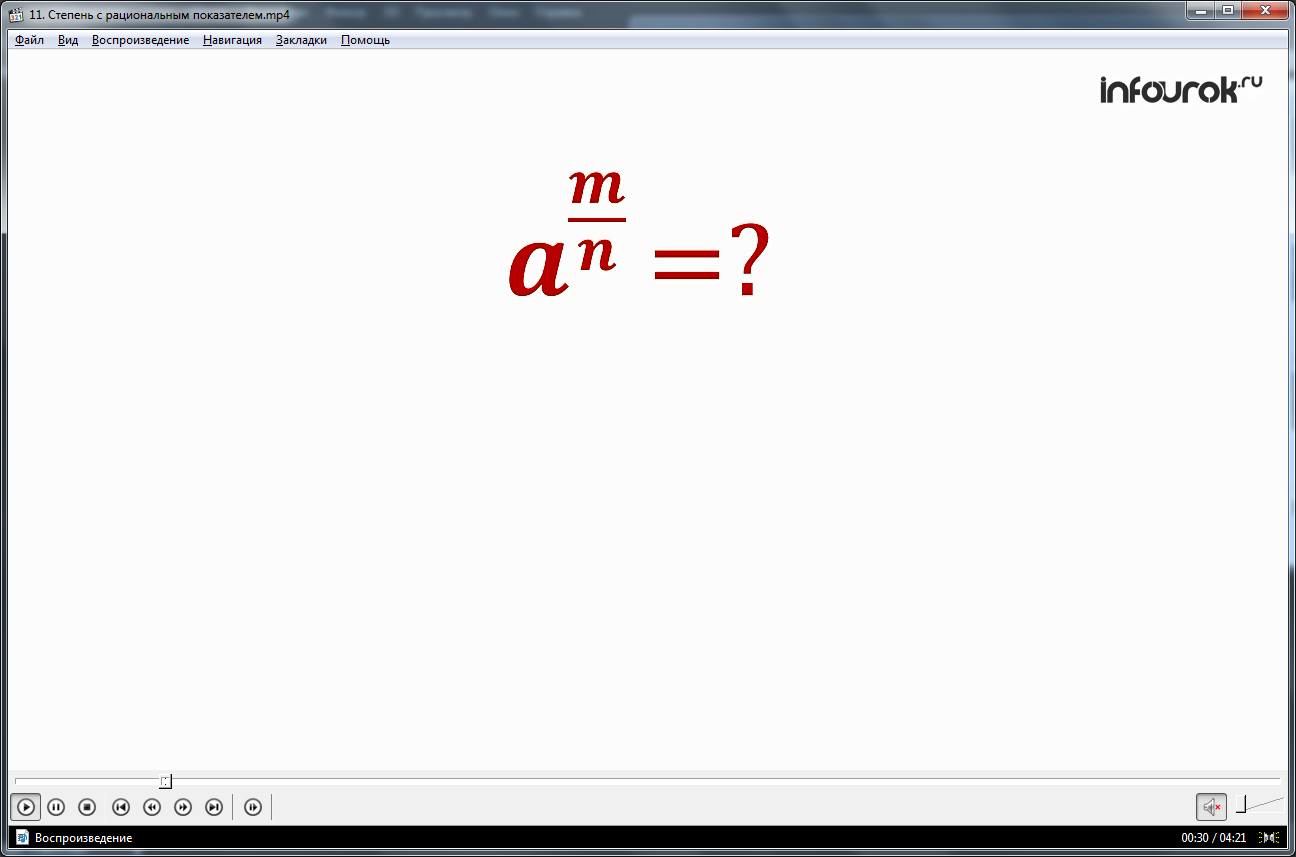
Видеоурок начинается с представления темы. Связывая изучения новой темы с ранее изученным материалом, предлагается вспомнить, чтоn√aиначе обозначается a1/nдля натурального n и положительного a. Данное представление корня n-степени отображается на экране. Далее предлагается рассмотреть, что значит выражение am/n, в котором a – положительное число, а m/n – некоторая дробь. Дается выделенное в рамке определение степени с рациональным показателем как am/n=n√am. При этом отмечено, что n может быть натуральным числом, а m – целым.
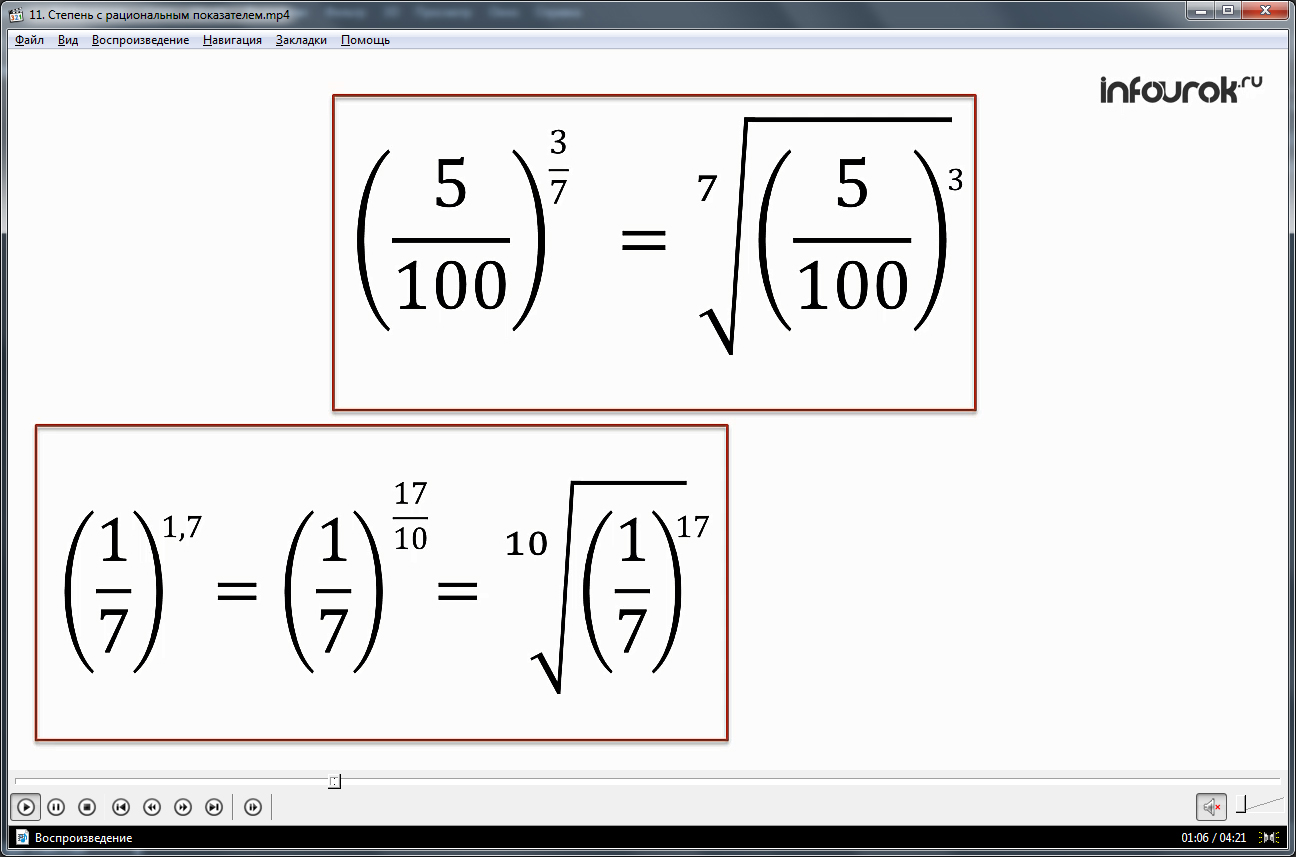
После определения степени с рациональным показателем ее смысл раскрывается на примерах: (5/100)3/7=7√(5/100)3. Также демонстрируется пример, в котором степень, представленная десятичной дробью, преобразуется в обычную дробь, чтобы быть представленной в виде корня: (1/7)1,7=(1/7)17/10=10√(1/7)17 и пример с отрицательным значением степени: 3-1/8=8√3-1.
Отдельно указывается особенность частного случая, когда основание степени – нуль. Отмечено, что данная степень имеет смысл только с положительным дробным показателем. В этом случае ее значение равно нулю: 0m/n=0.
Отмечена еще одна особенность степени с рациональным показателем – то, что степень с дробным показателем не может рассматриваться с дробным показателем. Приведены примеры некорректной записи степени: (-9)-3/7, (-3)-1/3, 0-1/5.
Далее в видеоуроке рассматриваются свойства степени с рациональным показателем. Замечено, что свойства степени с целым показателем будут также справедливы и для степени с рациональным показателем. Предлагается вспомнить перечень свойств, которые также справедливы в данном случае:
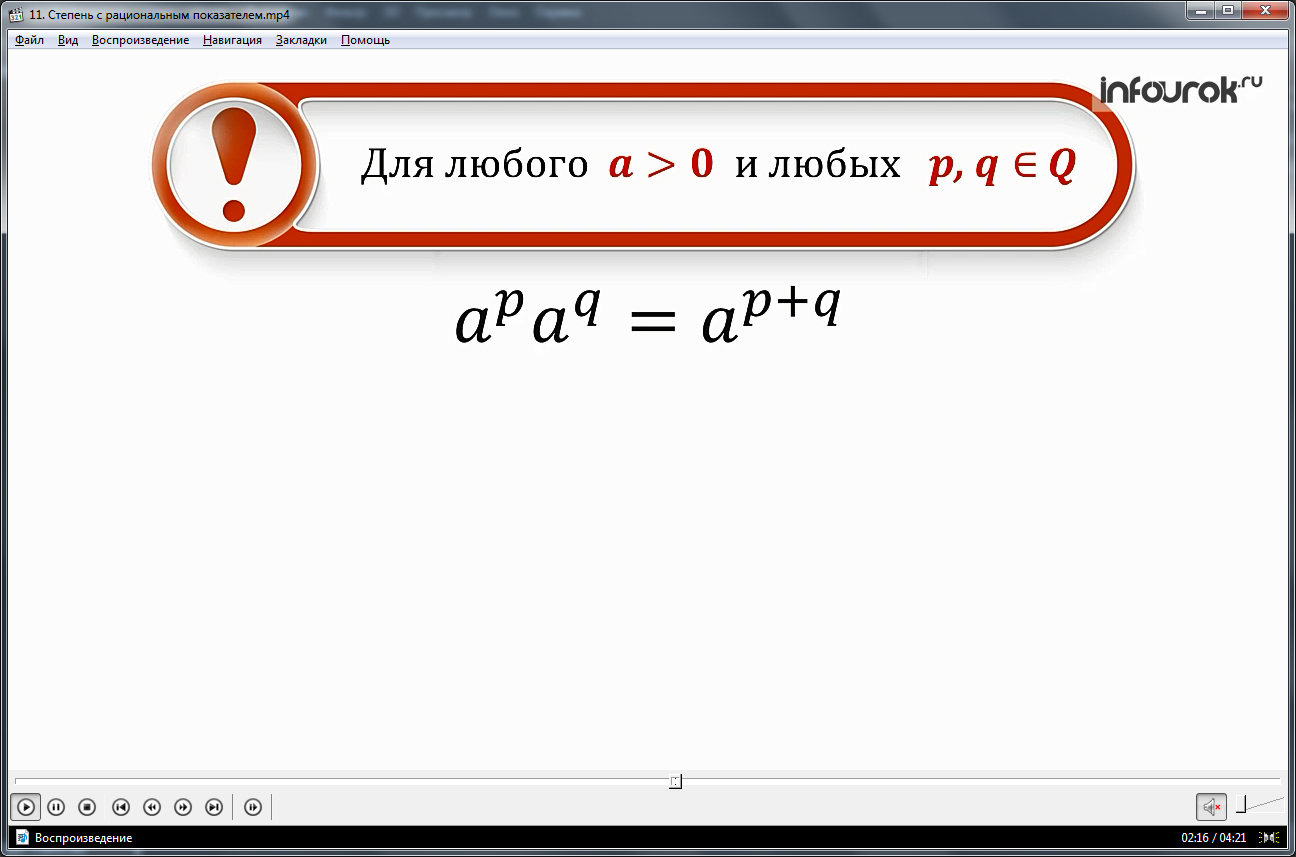
- При умножении степеней с одинаковыми основаниями их показатели складываются: apaq=ap+q.
- Деление степеней с одинаковыми основаниями сводится к степени с данным основанием и разностью показателей степеней: ap:aq=ap-q.
- Если возвести степень в некоторую степень, то в итоге получаем степень с данным основанием и произведением показателей: (ap)q=apq.
Все данные свойства справедливы для степеней с рациональными показателями p, q и положительным основанием a>0. Также верными остаются преобразования степени при раскрытии скобок:
- (ab)p=apbp – возведение в некоторую степень с рациональным показателем произведения двух чисел сводится к произведению чисел, каждое из которых возведено в данную степень.
- (a/b)p=ap/bp – возведение в степень с рациональным показателем дроби сводится к дроби, числитель и знаменатель которой возведены в данную степень.
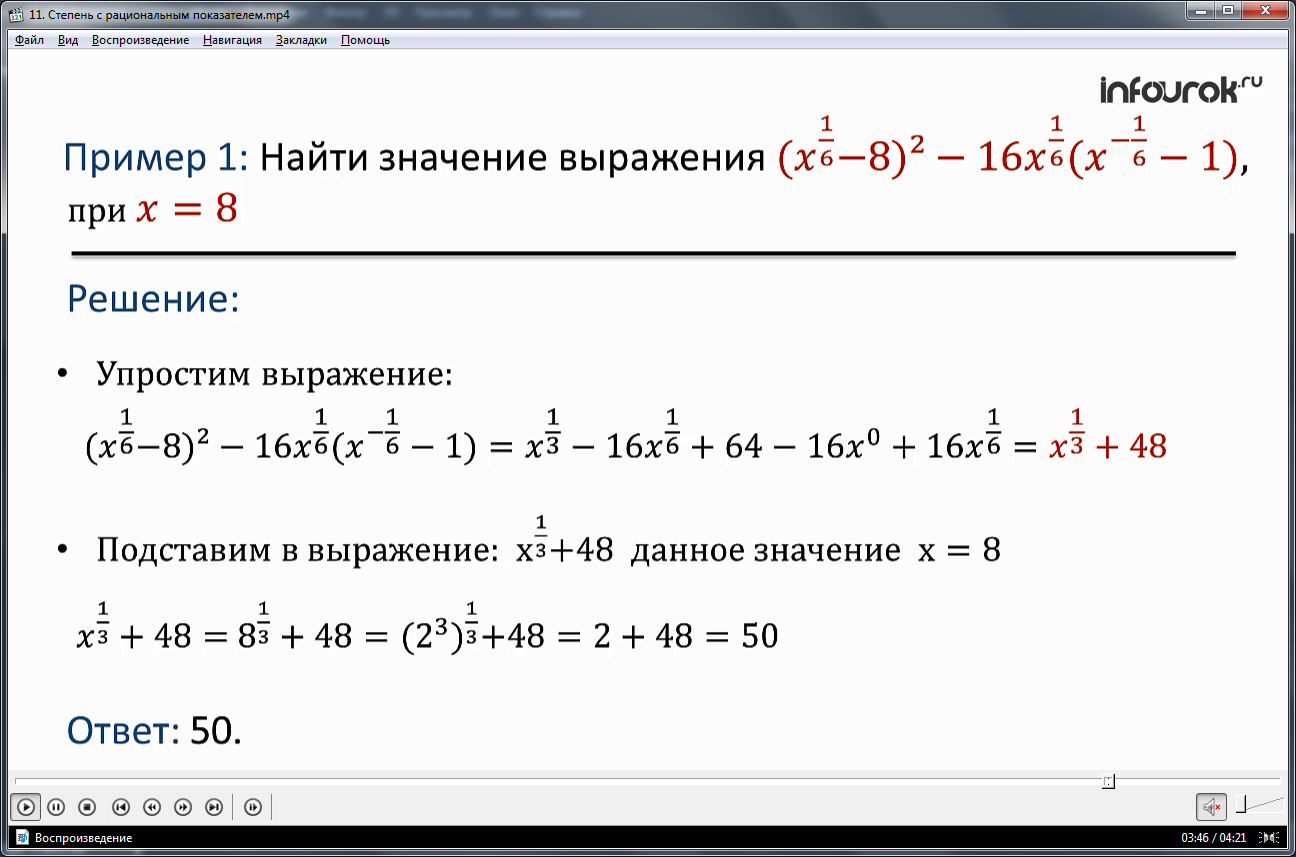
В видеоуроке рассматривается решение примеров, в которых используются рассмотренные свойства степеней с рациональным показателем. В первом примере предлагается найти значение выражения, в котором содержатся переменные х в дробной степени: (х1/6-8)2-16х1/6(х-1/6-1). Несмотря на сложность выражения, с применением свойств степеней оно решается достаточно просто. Решение задания начинается с упрощения выражения, в котором используется правило возведения степени с рациональным показателем в степень, а также перемножение степеней с одинаковым основанием. После подстановки заданного значения х=8 в упрощенное выражение х1/3+48, легко получить значение – 50.
Во втором примере требуется сократить дробь, числитель и знаменатель которой содержать степени с рациональным показателем. Используя свойства степени, выделяем из разности множитель х1/3, который затем сокращается в числителе и знаменателе, а используя формулу разности квадратов, на множители раскладывается числитель, что дает еще сокращения одинаковых множителей в числителе и знаменателе. Итогом таких преобразований становится короткая дробь х1/4+3.
Видеоурок «Степень с рациональным показателем» может быть использован вместо объяснения учителем новой темы урока. Также данное пособие содержит достаточно полную информацию для самостоятельного изучения учеником. Материал может быть полезен и при дистанционном обучении.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7449 |
| Номер материала | 658 |