
Урок «Степенные функции, их свойства и графики»

Краткое описание документа:
На прошлом занятии мы повторили и обобщили знания по теме «Понятие о показателе степени».
Вспомним, что если - пэ делённое на ку обыкновенная дробь, причём ку не равно единице и а больше или равно нулю, то под выражением а в степени пэ делённое на ку понимают корень степени ку из а в степени пэ.
Например, число одна целая три десятых в степени три седьмых можно записать как, корень седьмой степени из числа одна целая три десятых в кубе.
Функции вида , где k-любое действительное число, принято называть степенными функциями.
Сегодня мы рассмотрим случай, если k-рациональный (дробный) показатель.
В курсе алгебры 7-9 классов вы изучали свойства и графики степенных функций с натуральным показателем. Функция (k-любое действительное число), степенная функция.
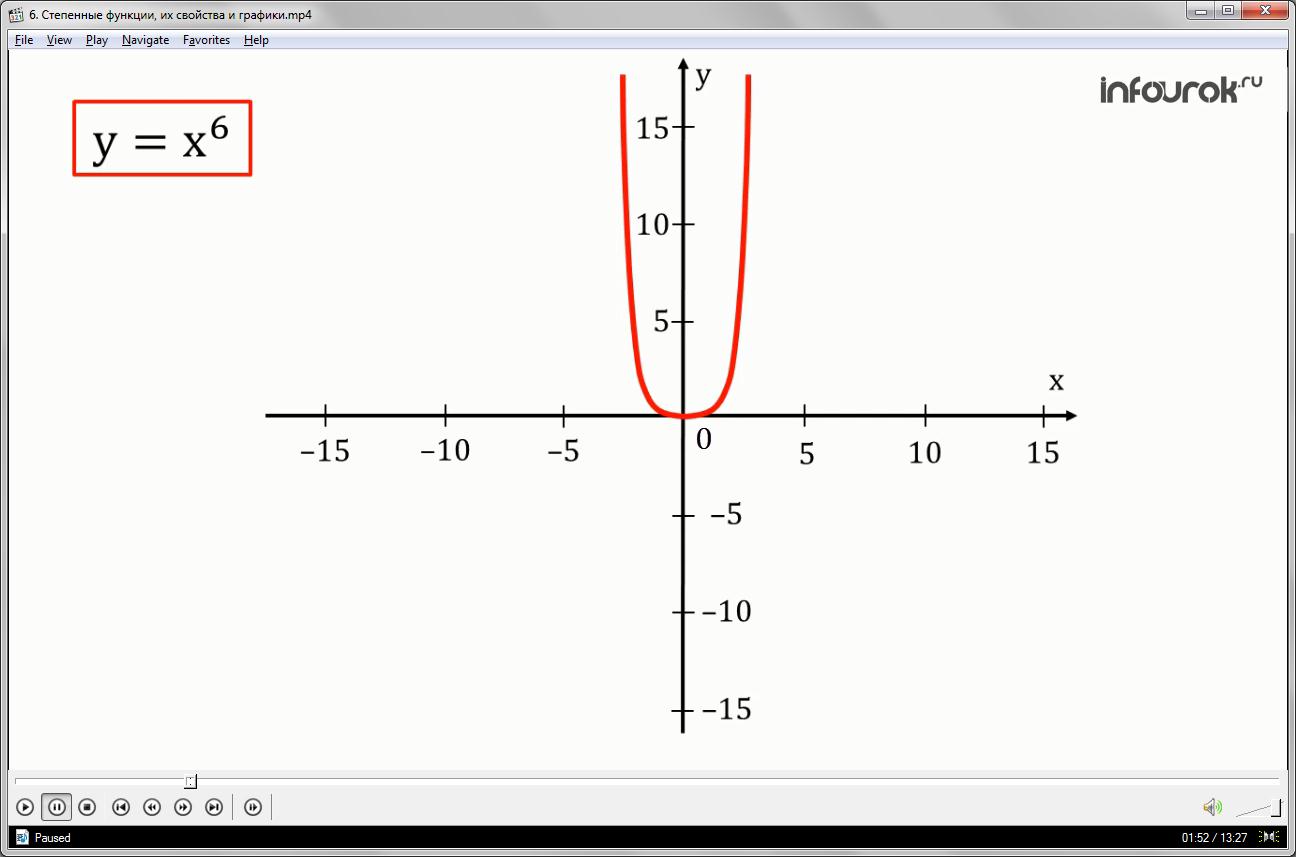
При k=n (n∈N), -степенная функция с натуральным показателем.
Вспомним графики таких функций.
Графиком функции или у=х (игрек равен икс в первой степени или игрек равный икс) является прямая.
Графиком функции (игрек равен икс в квадрате) является парабола.
Графиком функции (игрек равен икс в кубе) является кубическая парабола.
График степенной функции (игрек равен икс в степени ка) в случае чётного k — похож на параболу. На рисунке показан график степенной функции при k равном шести.
График степенной функции (игрек равен икс в степени ка) в случае нечётного k – похож на кубическую параболу. На рисунке показан график степенной функции при k равном семи.
В случае если в показателе степенной функции целое отрицательное число, то получим функцию вида: игрек равное икс в степени минус эн или игрек равен один делённое на икс в энной степени.
Если n — чётное число, то график имеет вид, изображённый на рисунке.
Где показана функция у=х–2, или у=
Если n — нечётное число, то график имеет следующий вид.
На чертеже изображена функция у=х–3, или у=
Если показатель степенной функции равен нулю, то функция примет вид: .Графиком такой функции является прямая, проходящая через ординату один и параллельная оси абсцисс.
При k=-n (n∈Z), -степенная функция с целым отрицательным показателем.
Рассмотрим степенную функцию (игрек равное икс в степени k), где k — отрицательное или положительное дробное число.
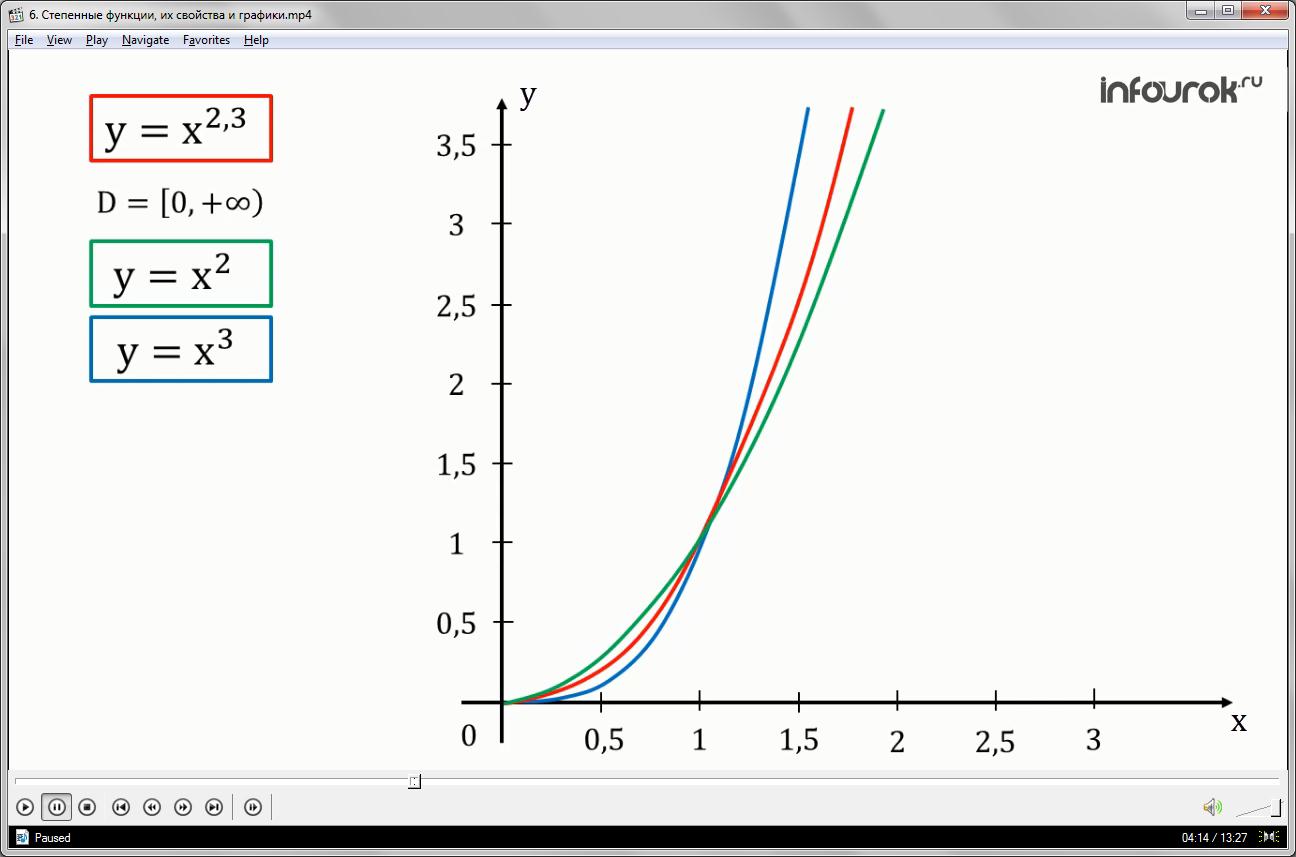
В качестве примера построим график степенной функции (игрек равен икс в степени две целых три десятых).
Областью её определения (то есть все значения, принимаемые икс) является луч с началом в точке ноль.
В этой области определения построим графики функций (игрек равное икс в квадрате) — это ветвь параболы, выделенная светло зелёным цветом и (игрек равное икс в кубе) – ветвь кубической параболы, выделенная тёмно-зелёным цветом.
Нетрудно убедиться в том, что на интервале (0;1) кубическая парабола расположена ниже параболы, а на открытом луче (1;+ ) — выше.
Обратите внимание, что графики функций (игрек равен икс в квадрате), (игрек равен икс в степени две целых три десятых) и (игрек равен икс в кубе) проходят через точки (0;0) и (1;1).
При остальных значениях аргумента икс график функции (игрек равен икс в степени две целых три десятых) находится между графиками функций (игрек равен икс в квадрате) и (игрек равен икс в кубе).
Аналогично обстоят дела с любой степенной функцией , где — неправильная дробь, то есть числитель m больше знаменателя n. Графиком этой функции является кривая, похожая на ветвь параболы.
Чем больше показатель функции k, тем «круче» устремлена ветвь.
На рисунке показан график функции игрек равен икс в степени семь вторых.
Таким образом, можно выделить следующие свойства степенной функции игрек равен икс в степени эм делённое на эн, где числитель m больше знаменателя n.
1. Областью определения являются значения икс от нуля до плюс бесконечности.
2. Функция не является ни чётной, ни нечётной.
3. Функция возрастает на всей области определения.
4.Снизу ограничена осью абсцисс, сверху не ограничена.
5.Функция принимает наименьшее значение нуль; наибольшего значения не имеет.
6. Функция непрерывна на всей области определения.
7. Областью значения функции являются значения игрек от нуля до плюс бесконечности.
8.Выпукла вниз.
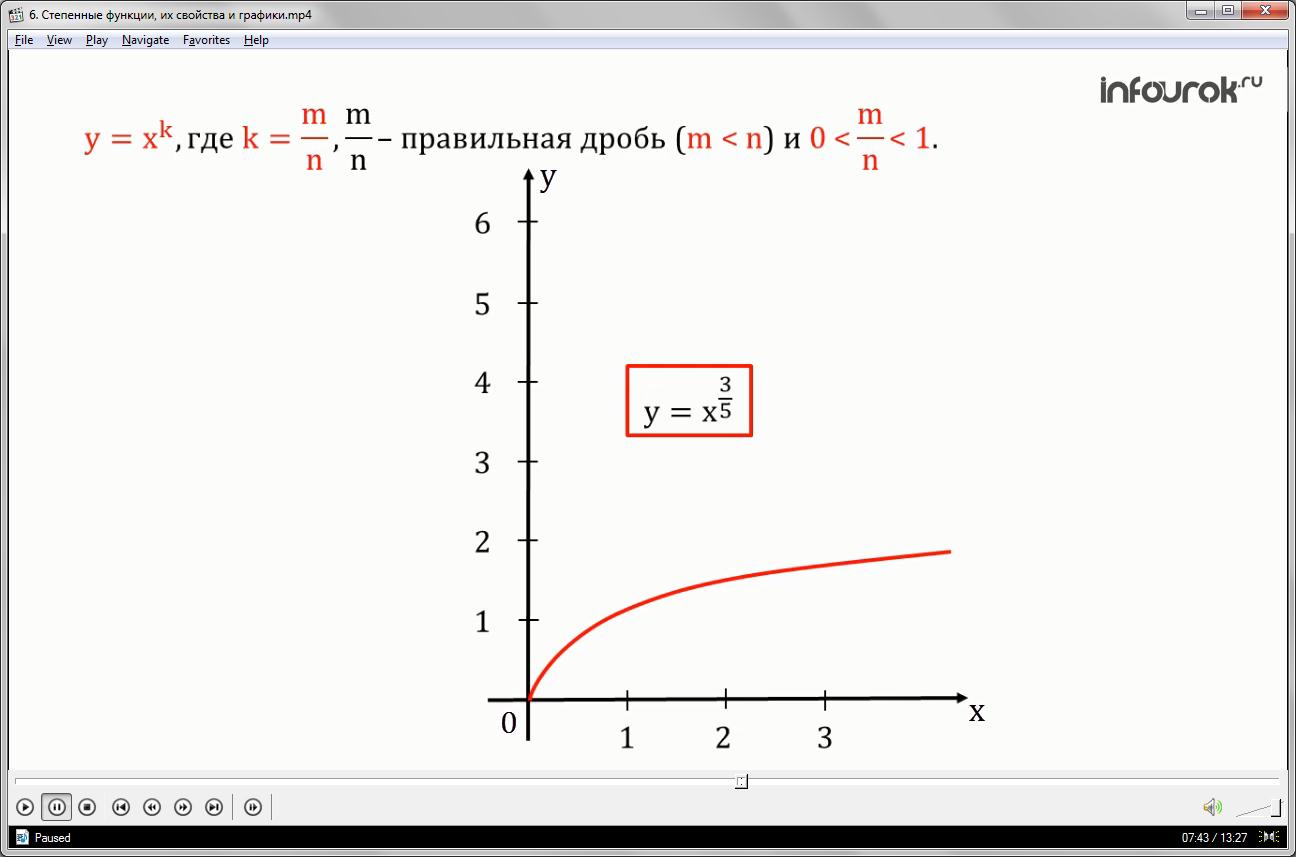
Построим график функции , где -правильная дробь(числитель меньше знаменателя) и 0< <1.
Рассмотренные ранее свойства и график функции (игрек равен корень энной степени из икс) или (игрек равен икс в степени один делённое на эн), применимы так же и к функции , где -правильная дробь и 0< <1.
Вспомним эти свойства:
1. Областью определения являются все значения икс от нуля до плюс бесконечности.
2. Функция не является ни чётной, ни нечётной.
3. Функция возрастает на всей области определения.
4. Снизу ограничена осью абсцисс, сверху не ограничена.
5. Функция принимает наименьшее значение ноль; наибольшего значения не имеет.
6. Функция непрерывна на всей области определения.
7. Областью значения функции являются значения игрек от нуля до плюс бесконечности.
8.Выпукла вверх. функция , где -правильная дробь(числитель меньше знаменателя) и 0<
2. Ни чётная ни нечётная.
3. Возрастает на .
4. Снизу ограничена осью абсцисс, сверху не ограничена.
5. yнаим=0; наибольшего значения не имеет.
6.Непрерывна.
7.
8. Выпукла вверх.
Рассмотрим следующий вид степенной функции — функцию вида: игрек равен икс в степени минус эм делённое на эн.
Ранее мы построили график степенной функции с целым отрицательным показателем игрек равен икс в степени минус k, где k – натуральное число.
В случае если икс больше ноля, график этой функции похож на ветвь гиперболы.
Аналогичным образом строится график любой степенной функции с отрицательным рациональным (дробным) показателем.
Следует иметь в виду, что график такой функции имеет две асимптоты: горизонтальную — игрек равен нулю и вертикальную асимптоту — икс равен нулю.
Итак, степенная функция игрек равен икс в степени минус эм делённое на эн обладает следующими свойствами (причём икс больше нуля, так как в случае отрицательного основания с отрицательным показателем степень выражения не имеет смысла):
1) Область определения — открытый луч от нуля до бесконечности.
2) Функция не является ни чётной, ни нечётной.
3) Функция убывает на всей области определения.
4) Снизу ограничена осью абсцисс, сверху не ограничена.
5) Функция не имеет наименьшего и наибольшего значения.
6) Функция непрерывна на всей области определения.
7) Областью значения функции являются значения игрек от нуля до плюс бесконечности.
8) Выпукла вниз.
Свойства степенной функции ( x 0):
1).
2). Ни чётная ни нечётная.
3). Убывающая.
4). Снизу ограничена осью абсцисс, сверху не ограничена.
5). Не имеет наименьшего и наибольшего значения.
6). Непрерывна на
7).
8). Выпукла вниз.
Вы уже знаете, что производная степенной функции вида игрек равен икс в степени эн, где n — натуральное число, равна n умноженное на икс в степени n минус один.
Аналогично можно вычислить производную степенной функции с рациональным показателем.
Таким образом, верна следующая теорема:
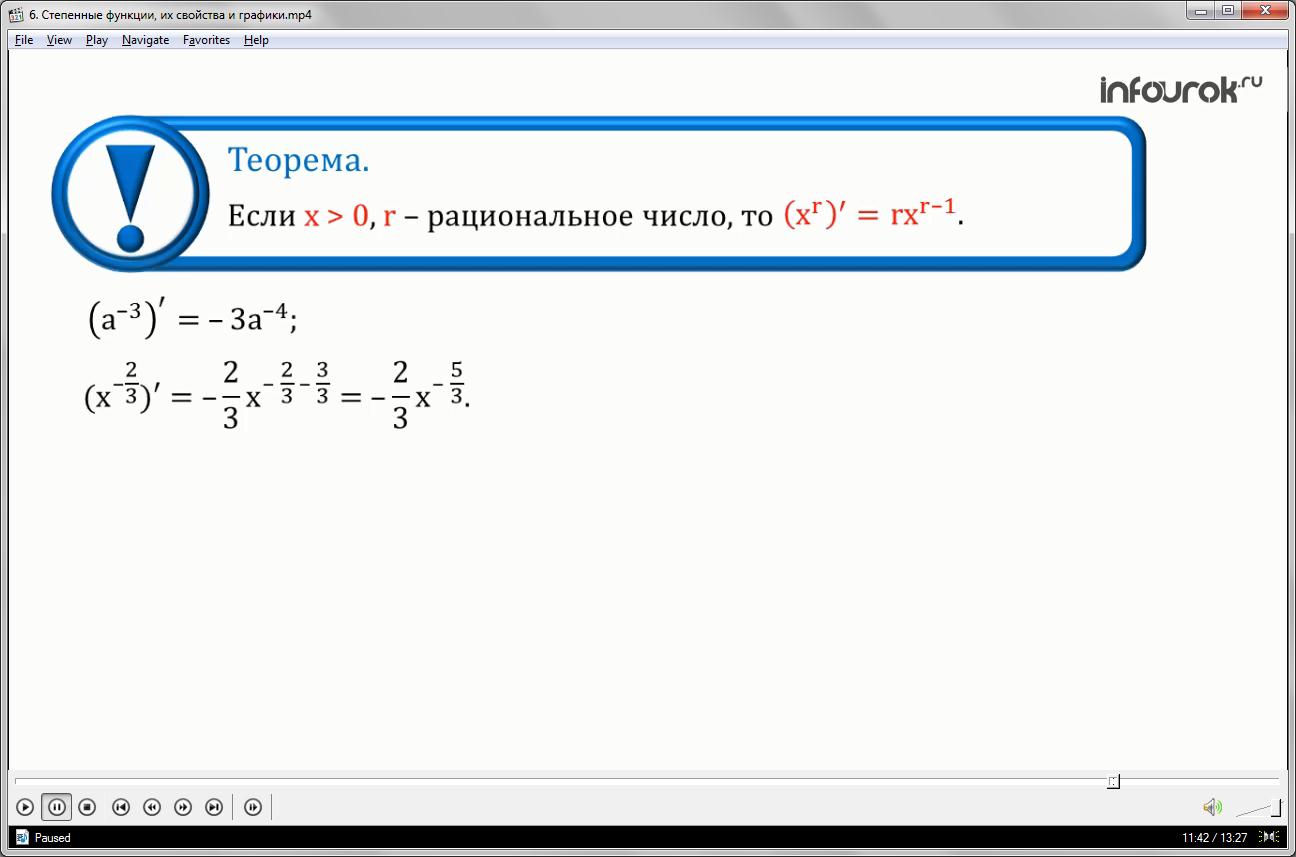
Если икс больше нуля и r — произвольное рациональное число, то производная степенной функции игрек равна икс в степени r, и вычисляется по формуле: производная икс в степени r равна r умноженное на икс в степени r минус один.
Например, производная а в минус третьей степени равна минус три а в степени минус четыре.
Производная икс в степени минус две третьих равна минус две третьих икс в степени минус пять третьих.
Здесь минус один представили в виде неправильной дроби три третьих, затем сложили дроби минус две третьих и минус три третьих.
Теорема: если x>0, r-рациональное число, то
Пример:
Не составляет труда получить соответствующую формулу для интегрирования степенной функции при r не равном одному. Итак, неопределённый интеграл от икс в степени r равен икс в степени r плюс один, делённое на r плюс один и плюс константа цэ.
Не сложно понять, что функция равна икс в степени r плюс один, делённое на r плюс один является первообразной для функции игрек равен икс в степени r. Формула для интегрирования степенной функции:
r≠1
Функция первообразная для функции .
Рассмотрим применение полученных знаний при построении графика степенной функции.
Пример:
Построить график функции игрек равен икс плюс два в степени одна вторая.
Решение:
1.Построим график функции икс в степени одна вторая. Это функция вида , где -правильная дробь (числитель меньше знаменателя) и 0< <1.График такой функции мы уже строили, на рисунке график выделен красным цветом.
2.Очевидно, что график функции игрек равен икс плюс два в степени одна вторая строится с помощью параллельного переноса относительно оси икс на две единицы влево. На рисунке график выделен зелёным цветом.
Пример :
Построить график функции
1. -частный случая для функции вида , где -правильная дробь(числитель меньше знаменателя) и 0< <1.
2. График получен параллельным переносом вдоль оси X на 2 единицы влево.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 14776 |
| Номер материала | 1055 |