
Урок «Свойства корня n-й степени»

Краткое описание документа:
Для чего нужна данная тема?
Изучив свойства корня n-ой степени, вы научитесь быстро и правильно проводить операцию по извлечению корня.
Сформулируем и докажем свойства только для неотрицательных значений переменных, находящихся под знаком корня.
Теорема 1: Корень n-ой степени (n=2, 3, 4,…) из произведения двух неотрицительных чисел равен произведению корней n-ой степени из этих чисел: <!--?mso-application progid="Word.Document"?--> 14nab"> = <!--?mso-application progid="Word.Document"?--> 14nanb">
(Корень энной степени из произведения равен произведению корней энной степени).
Доказательство: Обозначим <!--?mso-application progid="Word.Document"?--> 14nab"> =m, <!--?mso-application progid="Word.Document"?--> 14na"> =s, <!--?mso-application progid="Word.Document"?--> 14nb"> =t и докажем равенство m=st, где m,s,t – неотрицательные числа.
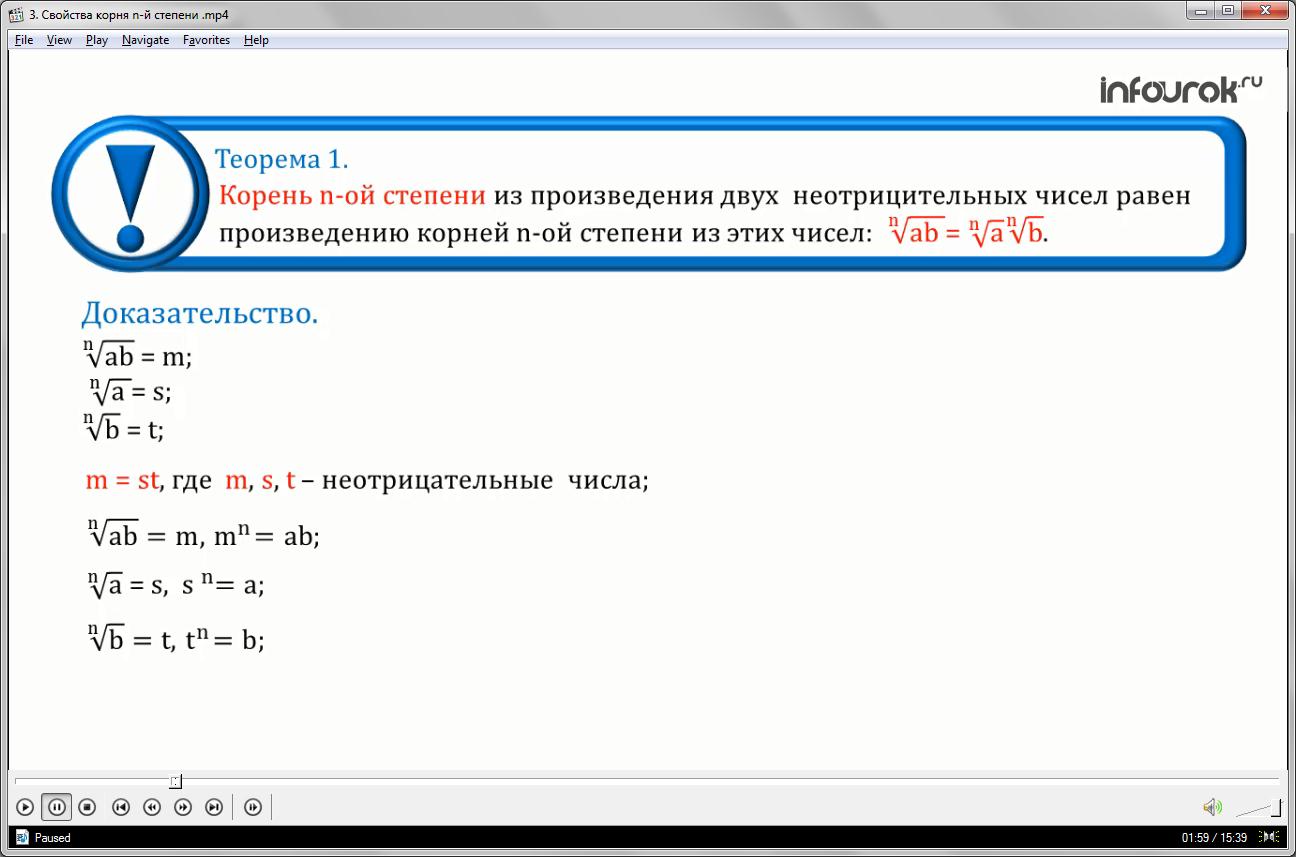
Воспользовавшись определением корня энной степени из числа, получим равенства:
<!--?mso-application progid="Word.Document"?--> 14nab=m, mn=ab; na"> =s, <!--?mso-application progid="Word.Document"?--> 14 s n=a; nb=t, tn=b"> .
<!--?mso-application progid="Word.Document"?--> 14Если mn=ab, sn=a, tn=b, то mn=sntn, то есть mn=(st)n"> , а значит m=st , так как если показатели степени одинаковы, то и основания степеней равны, что и требовалось доказать.
Для наглядности оформим доказательство в виде таблицы:
|
Введение новых переменных |
Определение корня n-ойстепени |
Доказательство |
|
<!--?mso-application progid="Word.Document"?--> 14nab=m"> <!--?mso-application progid="Word.Document"?--> 14na"> =s <!--?mso-application progid="Word.Document"?--> 14nb=t"> |
<!--?mso-application progid="Word.Document"?--> 14mn=ab"> <!--?mso-application progid="Word.Document"?--> 14sn=a"> <!--?mso-application progid="Word.Document"?--> 14tn=b"> |
<!--?mso-application progid="Word.Document"?--> 14nab"> = <!--?mso-application progid="Word.Document"?--> 14nanb"> <!--?mso-application progid="Word.Document"?--> 14mn=sntn,"> <!--?mso-application progid="Word.Document"?--> 14mn=stn"> m=st
|
|
Доказать: m=st |
Замечание 1: Данная теорема справедлива и когда подкоренным выражением является произведение более двух неотрицательных чисел
Теорема 2: Если <!--?mso-application progid="Word.Document"?--> 14 a≥0, b>0, Рё n-натуральное число, большее единицы, то справедливо равенство">
<!--?mso-application progid="Word.Document"?--> 14nab=nanb">
(корень энной степени из частного а на бэ равен частному корней энной степени из а и бэ).
Доказательство оформим в виде таблицы аналогично доказательству первой теоремы.
Введем новые переменные и обозначим
<!--?mso-application progid="Word.Document"?--> 14nab=m"> , <!--?mso-application progid="Word.Document"?--> 14na"> =s, <!--?mso-application progid="Word.Document"?--> 14nb"> =t и докажем равенство <!--?mso-application progid="Word.Document"?--> 14m=st"> , где m,s,t – неотрицательные числа.
Воспользовавшись определением корня энной степени из числа, получим равенства:
если <!--?mso-application progid="Word.Document"?--> 14nab=m, то mn=ab"> <!--?mso-application progid="Word.Document"?--> 14;">
<!--?mso-application progid="Word.Document"?--> 14если na"> =s, то <!--?mso-application progid="Word.Document"?--> 14s n=a, если nb=t, то tn=b.">
Заменим новыми переменными корень энной степени из частного а на бэ и частное корней энной степени из а и бэ, получим, что
Запомните, что каждая формула в алгебре выполняется в обе стороны, т.е. слева направо так и справа налево.
Пример 1: Вычислите <!--?mso-application progid="Word.Document"?--> 14416в€™81в€™256">
Решение: Применим теорему 1 <!--?mso-application progid="Word.Document"?--> 14(nab"> = <!--?mso-application progid="Word.Document"?--> 14nanb) "> и получим:
<!--?mso-application progid="Word.Document"?--> 14416в€™81в€™256"> = <!--?mso-application progid="Word.Document"?--> 14416в€™481в€™4256">
<!--?mso-application progid="Word.Document"?--> 14Рзвлечем корень четвертой степени: 416=2, 481 =3, 4256=4">
Тогда получим произведение <!--?mso-application progid="Word.Document"?--> 142в€™3в€™4=24">
<!--?mso-application progid="Word.Document"?--> 14416в€™81в€™256"> = <!--?mso-application progid="Word.Document"?--> 14416в€™481в€™4256=2в€™3в€™4=24"> .
Пример 2: Вычислите <!--?mso-application progid="Word.Document"?--> 14571932">
Решение: Переведем смешанную дробь в неправильную, для этого целую часть умножим на знаменатель и прибавим числитель, результат произведения запишем в числитель, а затем применим теорему 2 «корень энной степени из частного а на бэ равен частному корней энной степени из а и бэ». В результате получилось <!--?mso-application progid="Word.Document"?--> 145243532"> . Извлечем корень пятой степени <!--?mso-application progid="Word.Document"?--> 145243=3"> ; <!--?mso-application progid="Word.Document"?--> 14532=2"> , получим <!--?mso-application progid="Word.Document"?--> 1432"> , извлечем целую часть и получим 1 <!--?mso-application progid="Word.Document"?--> 1412или 1,5"> .
<!--?mso-application progid="Word.Document"?--> 14571932"> = <!--?mso-application progid="Word.Document"?--> 1457в€™32+1932=524332=5243532=32"> =1 <!--?mso-application progid="Word.Document"?--> 1412=1,5">
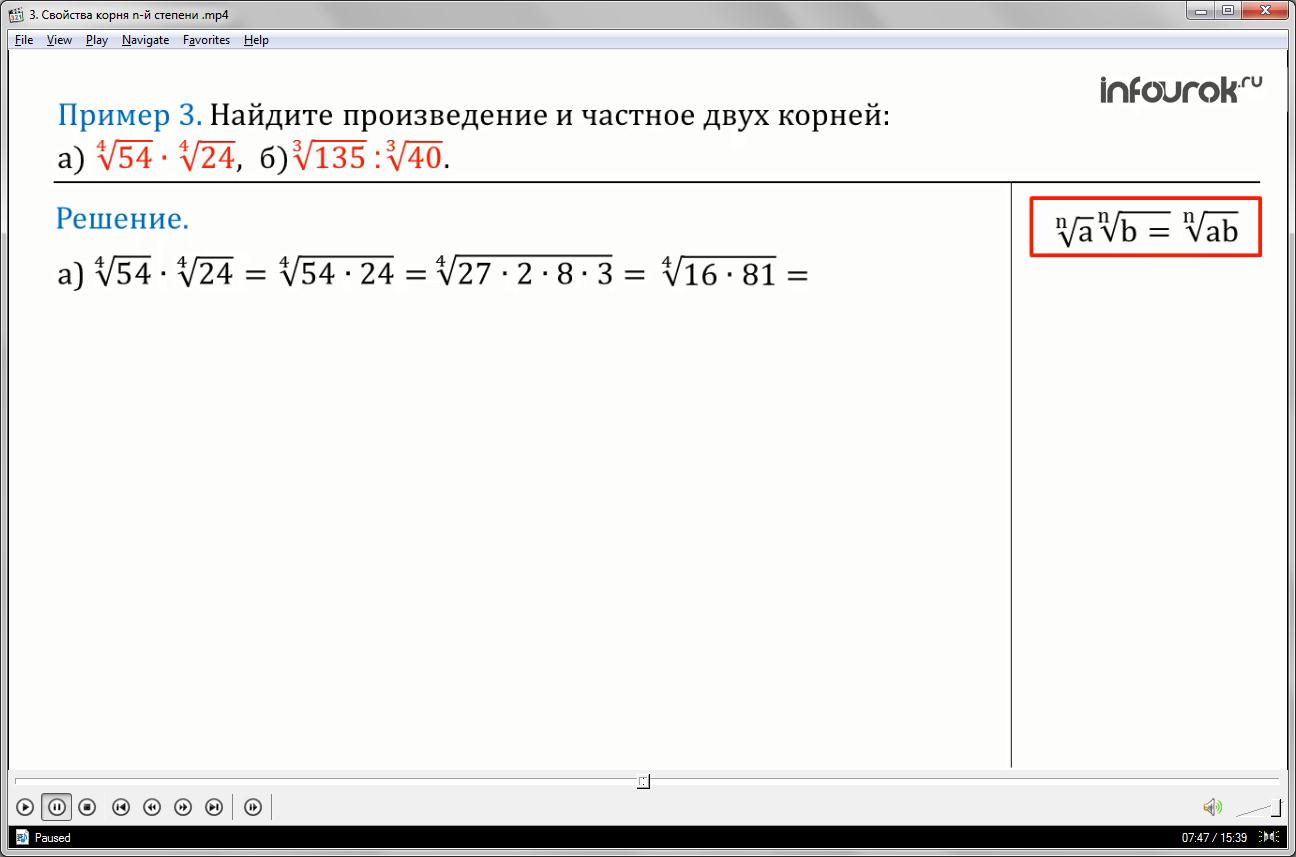
Пример 3: Вычислите <!--?mso-application progid="Word.Document"?--> 14Р°) 454в€™424, Р±)3135 Чѓ340"> (найдите произведение и частное двух корней).
а) Согласно свойству, произведение двух корней равно корню из произведения, т.е. применим теорему 1 в обратном порядке <!--?mso-application progid="Word.Document"?--> 14nanb=nab">
Получим, что <!--?mso-application progid="Word.Document"?--> 14 454в€™424=454в€™24"> =
( <!--?mso-application progid="Word.Document"?--> 14разложим 54 и 24 на множители: 54=27∙2 и 24=8∙3)">
<!--?mso-application progid="Word.Document"?--> 14=427в€™2в€™8в€™3"> =
(заметим, что <!--?mso-application progid="Word.Document"?--> 142в€™8=16 Рё 27в€™3=81"> )
<!--?mso-application progid="Word.Document"?--> 14=416в€™81">
<!--?mso-application progid="Word.Document"?--> 14(извлечем корень четвертой степени из 416=2, 481=3)">
<!--?mso-application progid="Word.Document"?--> 14 и найдем значение выражения:произведение двух и трех равно 6.">
<!--?mso-application progid="Word.Document"?--> 14454в€™424=454в€™24=427в€™2в€™8в€™3=416в€™81=416в€™481=2в€™3=6">
б) <!--?mso-application progid="Word.Document"?--> 14 3135Чѓ340"> = <!--?mso-application progid="Word.Document"?--> 14313540=3278=32738=32"> =1,5
Согласно свойству, частное корней равно корню из частного, т.е. применим теорему 2 в обратном порядке: <!--?mso-application progid="Word.Document"?--> 14nanb=nab">
Сократим полученную дробь на 5 и получим: <!--?mso-application progid="Word.Document"?--> 143278"> ; воспользуемся еще раз теоремой 2, вычислим <!--?mso-application progid="Word.Document"?--> 14327"> = 3 и <!--?mso-application progid="Word.Document"?--> 1438"> = 2,
найдем значение выражения <!--?mso-application progid="Word.Document"?--> 1432 "> =1,5.
Теорема 3: Если <!--?mso-application progid="Word.Document"?--> 14а≥0, k-натуральное число Рё n-натуральное число, большее единицы, ">
<!--?mso-application progid="Word.Document"?--> 14то справедливо равенство nak=nak ">
Другими словами, чтобы возвести корень в натуральную степень, достаточно возвести в эту степень подкоренное выражение.
Это следствие теоремы 1. Пусть <!--?mso-application progid="Word.Document"?--> 14k=4, тогда "> воспользуемся определением степени, получим
<!--?mso-application progid="Word.Document"?--> 14na4 =naв€™naв€™naв€™na"> =
применим теорему 1 в обратном порядке, получим
<!--?mso-application progid="Word.Document"?--> 14=naв€™aв€™aв€™a=">
и снова воспользуемся определением степени
<!--?mso-application progid="Word.Document"?--> 14=na4"> .
(четвертая степень корня энной степени из а равна произведению четырех корней энной степени из а, равно корню энной степени из произведения четырех а, равно корню энной степени из а в четвертой степени).
Заметим, что вместо <!--?mso-application progid="Word.Document"?--> 14k"> можно принять любое другое натуральное число.
Теорема 4: Если <!--?mso-application progid="Word.Document"?--> 14а≥0 Рё k, n-натуральные числа, большие единицы, то справедливо равенство:">
<!--?mso-application progid="Word.Document"?--> 14nka=nka">
<!--?mso-application progid="Word.Document"?--> 14Другими словами, чтобы извлечь корень из корня, достаточно ">
<!--?mso-application progid="Word.Document"?--> 14перемножить показатели корней.">
Введем новые переменные, обозначим <!--?mso-application progid="Word.Document"?--> 14nka"> =m и <!--?mso-application progid="Word.Document"?--> 14nka"> =s и докажем равенство m=s, где m, s – неотрицательные числа.
Воспользовавшись определением корня энной степени из числа, получим равенства:
<!--?mso-application progid="Word.Document"?--> 14nka"> =m, <!--?mso-application progid="Word.Document"?--> 14 mn=ka"> и <!--?mso-application progid="Word.Document"?--> 14mnk=a"> ; <!--?mso-application progid="Word.Document"?--> 14nka"> =s, значит, <!--?mso-application progid="Word.Document"?--> 14 snk=a"> .
Если <!--?mso-application progid="Word.Document"?--> 14mnk=a "> и <!--?mso-application progid="Word.Document"?--> 14 snk=a"> , то <!--?mso-application progid="Word.Document"?--> 14 mnk=snk"> ,
в левой части последнего равенства применим свойство степени (при возведении степени в степень показатели перемножаются), получим
<!--?mso-application progid="Word.Document"?--> 14mnk=snk"> .
А так как показатели степени равны, то и основания степеней будут равны, т.е.
m=s,
что и требовалось доказать.
Рассмотрим применение данных теорем.
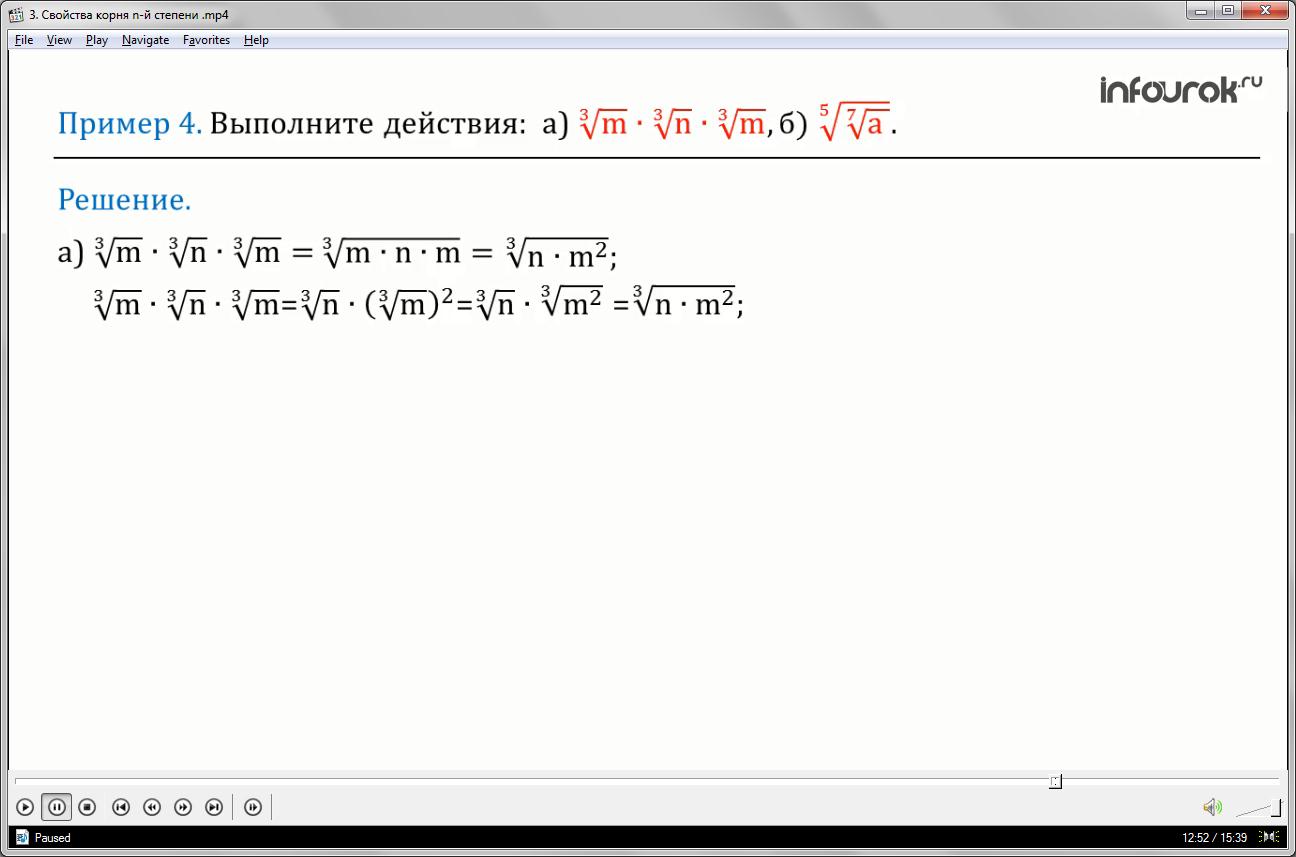
Пример 4: Выполните действия а) <!--?mso-application progid="Word.Document"?--> 143mв€™3nв€™3m, произведение корней третьей степени РёР· СЌРј, РёР· СЌРЅ Рё РёР· СЌРј ">
<!--?mso-application progid="Word.Document"?--> 14b) 57а (корень пятой степени из корня седьмой степени из а)">
а) <!--?mso-application progid="Word.Document"?--> 143mв€™3nв€™3m"> =
применим свойство корней: произведение корней равно корню из произведения, получим
<!--?mso-application progid="Word.Document"?--> 14=3mв€™nв€™m=">
применим свойство степеней: при умножении степеней их показатели складываются, а основание остается тем же, имеем
<!--?mso-application progid="Word.Document"?--> 14=3nв€™m2"> .
(произведение корней третьей степени из эм, из эн и из эм равно корню третьей степени из произведения эм на эн и на эм равно корню третьей степени из произведения эн и квадрата эм)
или <!--?mso-application progid="Word.Document"?--> 143mв€™3nв€™3m"> = <!--?mso-application progid="Word.Document"?--> 143nв€™3m2"> = <!--?mso-application progid="Word.Document"?--> 143nв€™3m2"> = <!--?mso-application progid="Word.Document"?--> 143nв€™m2">
(произведение корней третьей степени из эм, из эн и из эм равно произведению корня третьей степени из эн на квадрат корня третьей степени из эм равно произведению корня третьей степени из эн на корень третьей степени из квадрата эм равно корню третьей степени из произведения эн и квадрата эм)
б) <!--?mso-application progid="Word.Document"?--> 1457Р°"> = <!--?mso-application progid="Word.Document"?--> 145в€™7Р°=35Р°"> (корень пятой степени из корня седьмой степени из а равен корню тридцать пятой степени из а, так как на основании теоремы 4: чтобы извлечь корень из корня нужно перемножить показатели корней)
Теорема 5: Если показатели корня и подкоренного выражения умножить или разделить на одно и тоже натуральное число, то значение корня не изменится:
<!--?mso-application progid="Word.Document"?--> 14npakp=nak">
Доказательство: Введем обозначения: пусть <!--?mso-application progid="Word.Document"?--> 14npakp"> =s и <!--?mso-application progid="Word.Document"?--> 14nak"> =m, тогда, используя определение корня, получим равенства <!--?mso-application progid="Word.Document"?--> 14snp=akp1, ">
<!--?mso-application progid="Word.Document"?--> 14mn=ak(2). "> Обе части второго равенства(2) возведем в степень р, в результате получим <!--?mso-application progid="Word.Document"?--> 14mnp=akp"> (3). Внимательно рассмотрев (1) и (3) равенства получим, что <!--?mso-application progid="Word.Document"?--> 14snp=mnp"> , а так как степени одинаковы, то и равны основания степеней, т.е. s=m , в связи с этим получаем искомое равенство:
<!--?mso-application progid="Word.Document"?--> 14npakp=nak">
Пример 6:Выполнить действия <!--?mso-application progid="Word.Document"?--> 1414m3в€™14mв€™14m5в€™14m">
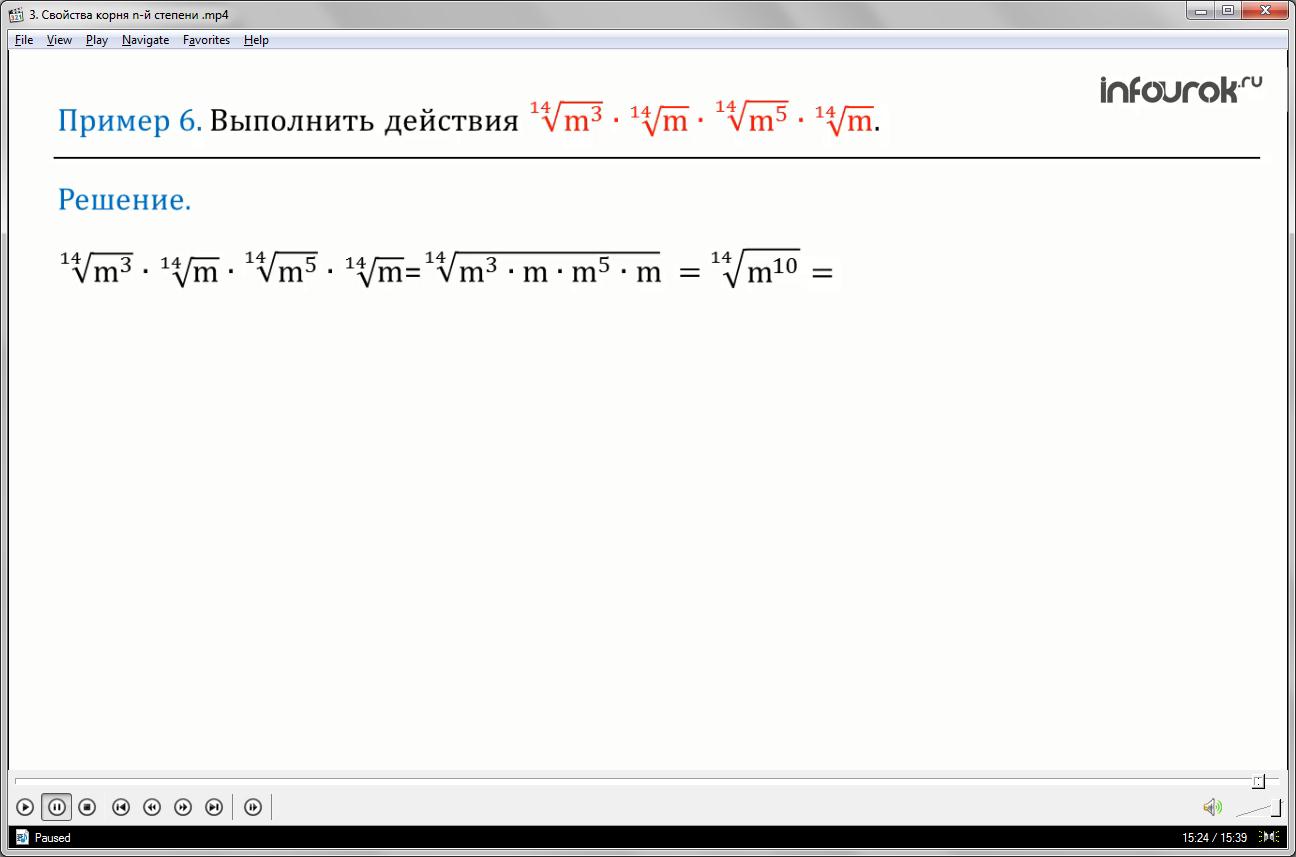
Решение <!--?mso-application progid="Word.Document"?--> 1414m3в€™14mв€™14m5в€™14m"> = <!--?mso-application progid="Word.Document"?--> 1414m3в€™mв€™m5в€™m=14m10=7m5">
Для преобразования выражения воспользуемся теоремой 1 в обратном порядке: произведению корней энной степени равен корень энной степени из произведения.
Таким образом, получим: произведение корней 14 степени равно корню 14 степени из произведения эм в кубе, эм, эм в пятой степени и эм. <!--?mso-application progid="Word.Document"?--> 1414m3в€™14mв€™14m5в€™14m"> = <!--?mso-application progid="Word.Document"?--> 1414m3в€™mв€™m5в€™m"> =
Согласно свойству степени, при умножении степеней их показатели складываются, а основание остается тем же, поэтому имеем
<!--?mso-application progid="Word.Document"?--> 14=14m10=">
Применим теорему 5: показатели корня и подкоренного выражения умножим или разделим на два
<!--?mso-application progid="Word.Document"?--> 14 =7В·2m5В·2"> =
и получим = <!--?mso-application progid="Word.Document"?--> 147m5"> .
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5317 |
| Номер материала | 1052 |