
Урок «Свойства логарифмов»

Краткое описание документа:
Мы уже познакомились с понятием логарифма.
Построили график функции у= и изучили свойства этой функции.
Сегодня мы познакомимся со свойствами логарифмов.
Обратим внимание, что все свойства, которые мы будем формулировать, доказываются только для положительных значений переменных, содержащихся под знаком логарифма.
Прежде чем перейти к свойствам, вспомним определение логарифма: (логарифм это показатель степени, в которую нужно возвести основание, что бы получить подлогарифмическое выражение).
Напомним три основных тождества:
- (логарифм а по основанию а равен единице, так как любое число в первой степени равно самому себе)
- (логарифм единицы по основанию а равен нулю, так как любое число в нулевой степени равно единице)
3. (логарифм а в степени эм по основанию а равен эм, так как а в степени эм равняется а в степени эм)
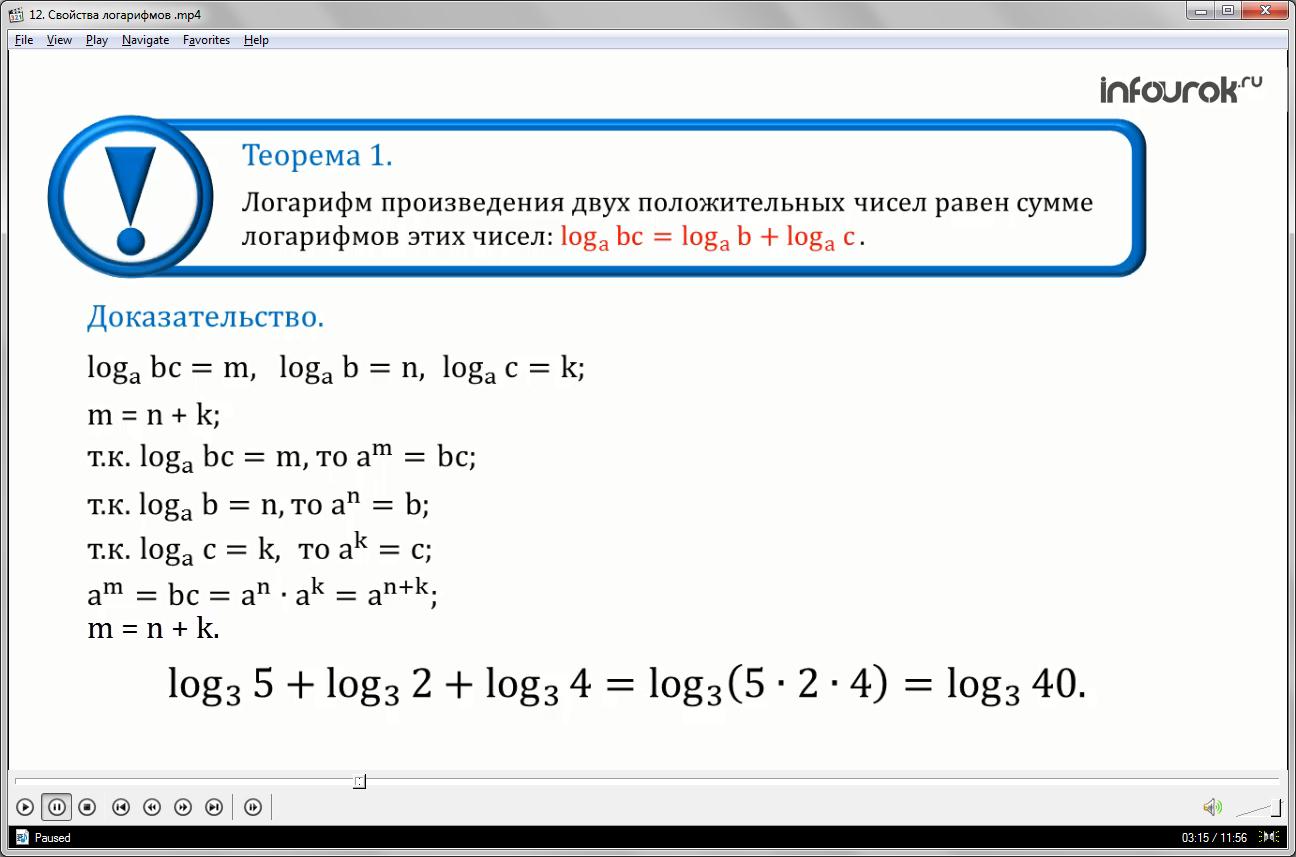
Теорема 1: Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел:
Доказательство: Если обозначить
(логарифм произведения бэ и цэ по основанию а равен эм, логарифм числа бэ по основанию а равен эн, логарифм числа цэ по основанию а равен ка), то необходимо доказать равенство m=n+k(эм равно сумме эн и ка)
Воспользуемся определением логарифма:
Т.к. то (а в степени эм, равно произведению бэ и цэ)
Т.к. (а в степени эн равно бэ)
Т.к. (а в степени ка равно цэ)
Введем замену и воспользуемся свойством степени, получим:
Так как основания равны и отличны от единицы, то равны и показатели степени, т.е. m=n+k , что и требовалось доказать.
Данная теорема справедлива и когда логарифмируемое выражение состоит из более двух множителей, например:
Теорема 2: Если a, b, c – положительные числа, причем , то справедливо равенство: = (логарифм частного, равен разности логарифмов числителя и знаменателя)
Оформим доказательство краткой записью, и прокомментируем каждый шаг, опираясь на полученные знания
Обозначим
(логарифм частного бэ на цэ по основанию а равен эм, логарифм числа бэ по основанию а равен эн, логарифм числа цэ по основанию а равен ка), значит, необходимо доказать равенство m=n - k(эм равно разности эн и ка)
Воспользуемся определением логарифма:
Т.к. то (а в степени эм, равно частному бэ на цэ)
Т.к. (а в степени эн равно бэ)
Т.к. (а в степени ка равно цэ)
Введем замену и воспользуемся свойством степени, получим:
Так как основания равны и отличны от единицы, то равны и показатели степени, т.е. m=n - k , что и требовалось доказать.
Приведем пример: (разность логарифма 36 по основанию 3 и логарифма 4 по основанию 3 равно логарифму частного 36 на 4,т.е. равно логарифму числа 9 по основанию три, девять представим как три в квадрате, следовательно, логарифм 9 по основанию 3 равен 2.)
Теорема 3: Если a,b –положительные числа, причем для любого числа r справедливо равенство
(логарифм степени равен произведению показателя степени на логарифм основания степени)
Обозначим
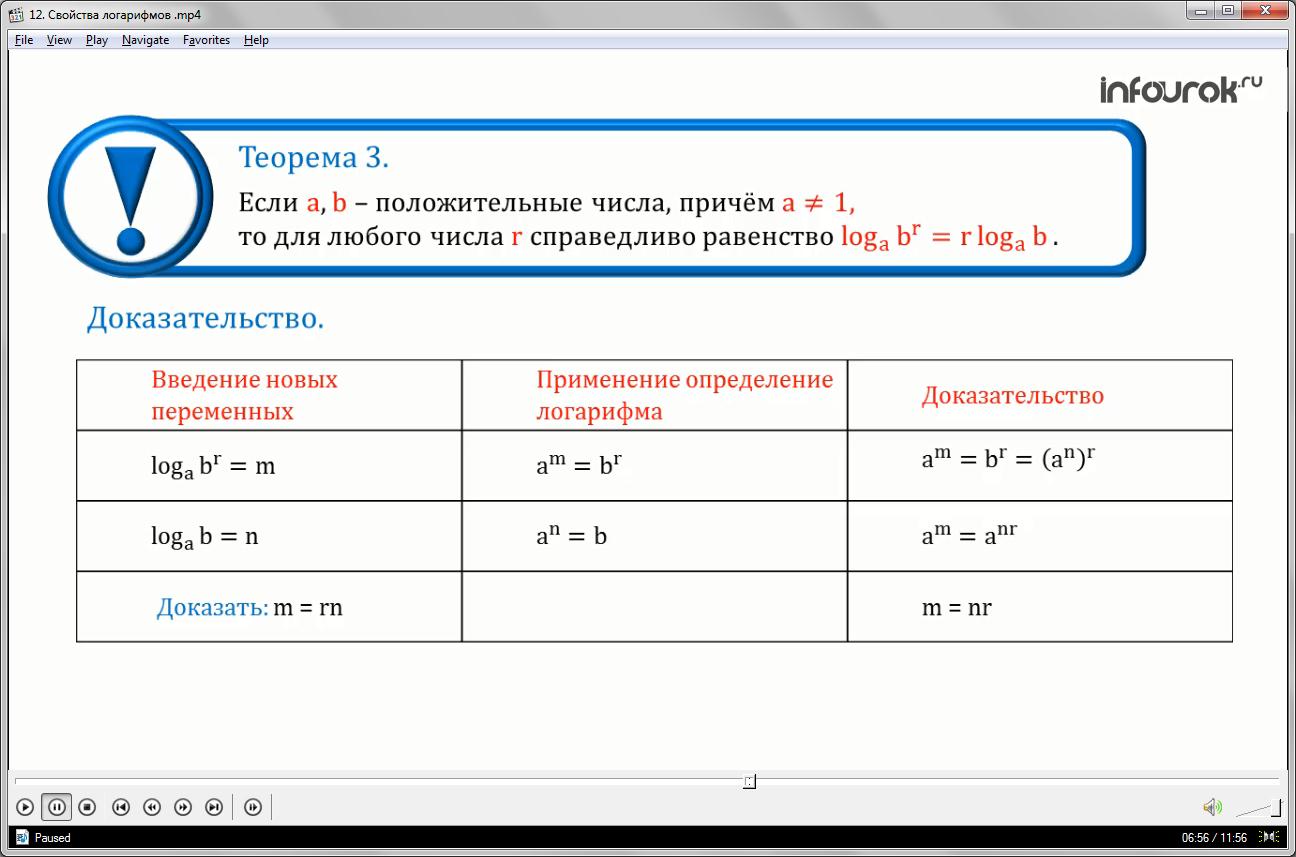
(логарифм числа бэ в степени эр по основанию а равен эм, логарифм числа бэ по основанию а равен эн), значит, необходимо доказать равенство m=rn(эм равно произведению эн и эр)
Воспользуемся определением логарифма:
(а в степени эм, равно бэ в степени эр)
Т.к. (а в степени эн равно бэ)
Введем замену и воспользуемся свойством степени, получим:
Так как основания равны и отличны от единицы, то равны и показатели степени, т.е. m=nr, что и требовалось доказать.
Пример: прологарифмируйте по основанию пять выражение (частное произведения двадцати пяти корней из пяти, а в шестой степени и бэ в седьмой степени на цэ в кубе).
Так как логарифм частного равен разности логарифмов числителя и знаменателя, то получим:
далее, применяя свойство логарифмов, по которому логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел, имеем
представим в виде степени:
затем логарифм степени равен произведению показателя степени на логарифм основания степени, поэтому
Теорема 4: Равенство
справедливо тогда и только тогда, когда m=n.
(логарифм числа эм по основанию а, равен логарифму числа эн по основанию а, тогда и только тогда, когда логарифмируемые выражения одинаковы)
Пример: Вычислите (пять в степени логарифм шестнадцати по основанию пять минус один).
Воспользуемся свойством степени (при делении степени вычитаются), тогда получим: =
далее воспользуемся определением логарифма (, логарифм — это показатель степени, в которую нужно возвести основание, чтобы получить подлогарифмическое выражение), тогда, поэтому продолжая вычисления, имеем
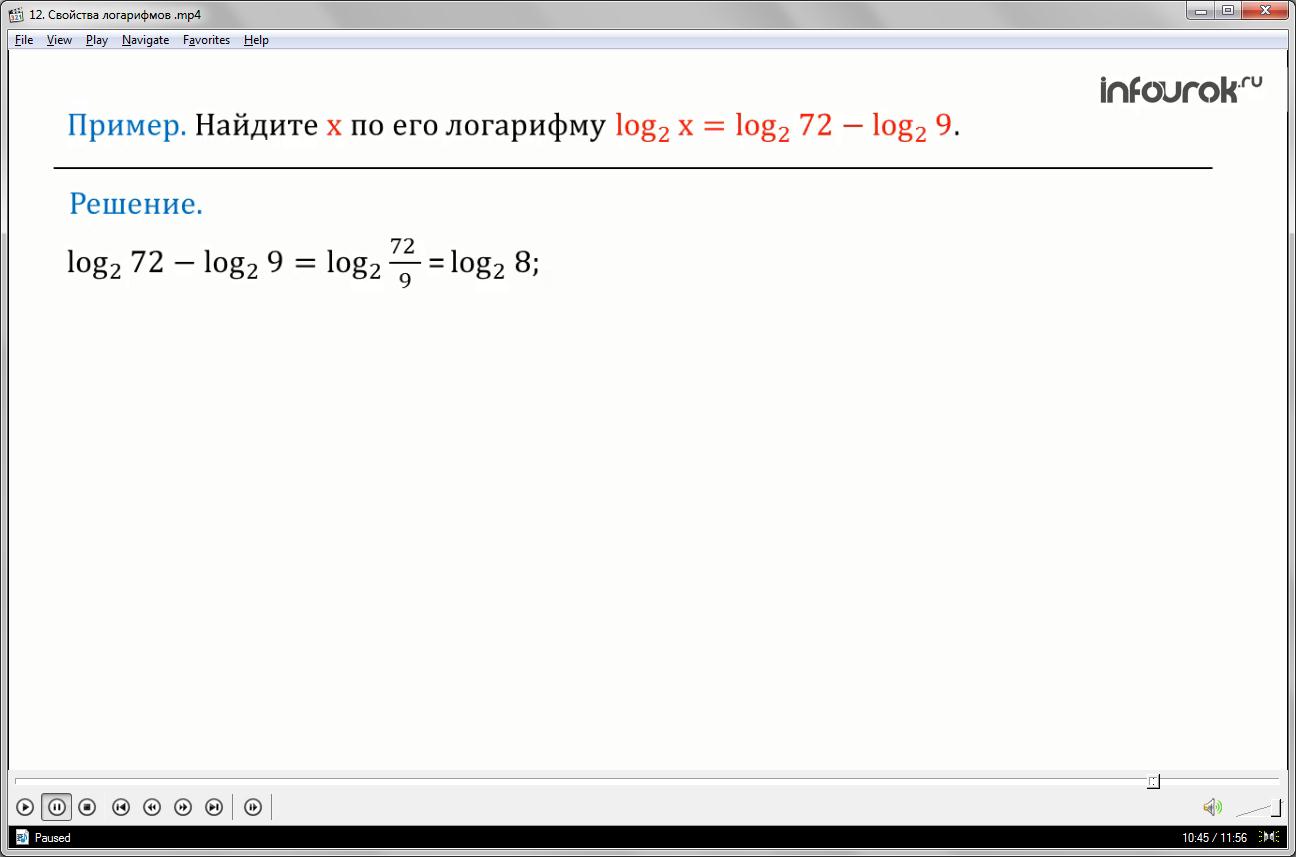
Пример: Найдите х (икс) по его логарифму
Применим свойство: логарифм частного равен разности логарифмов числителя и знаменателя, поэтому =,
А так как по теореме 4 логарифмы по одному основанию равны тогда и только тогда, когда логарифмируемые выражения одинаковы, то имеем
из того, что следует, что х=8.
Пример 4: Известно, что
(логарифм двух по основанию три равен а, логарифм пяти по основанию три равен бэ. Выразите логарифм пятидесяти по основанию три через а и бэ)
Пятьдесят заменим произведением двух множителей кратных двум и пяти; перейдем к сумме логарифмов; применим теорему 3 — логарифм степени равен произведению показателя степени на логарифм основания степени; произведем замену, воспользовавшись условием.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5170 |
| Номер материала | 1061 |