
Урок "Свойства прямоугольного параллелепипеда"

Краткое описание документа:
Видеоурок «Свойства прямоугольного параллелепипеда» демонстрирует теоремы геометрии и их доказательство, описывающие важные свойства прямоугольного параллелепипеда, используемые в решении геометрических задач. Задача видеоурока – наглядно продемонстрировать учебный материал, способствовать его лучшему запоминанию и пониманию учениками. Видео может быть использовано для сопровождения объяснения учителя в качестве наглядного пособия. Также данный видеоурок может стать полноценной частью урока математики вместо объяснения нового материала учителем.
При помощи анимации в демонстрации изучаемый материал подается структурировано, последовательно, выполняемые построения приближены к проведению традиционных построений на доске. Однако при этом все рисунки, текст хорошо видны, при необходимости важные понятия и детали построений выделяются цветом. Демонстрация дополнена иллюстрациями. При помощи озвучивания видео дополнено комментариями преподавателя, при введении новых понятий совмещение озвучивания текста с отображения его на доске способствует лучшему запоминанию.
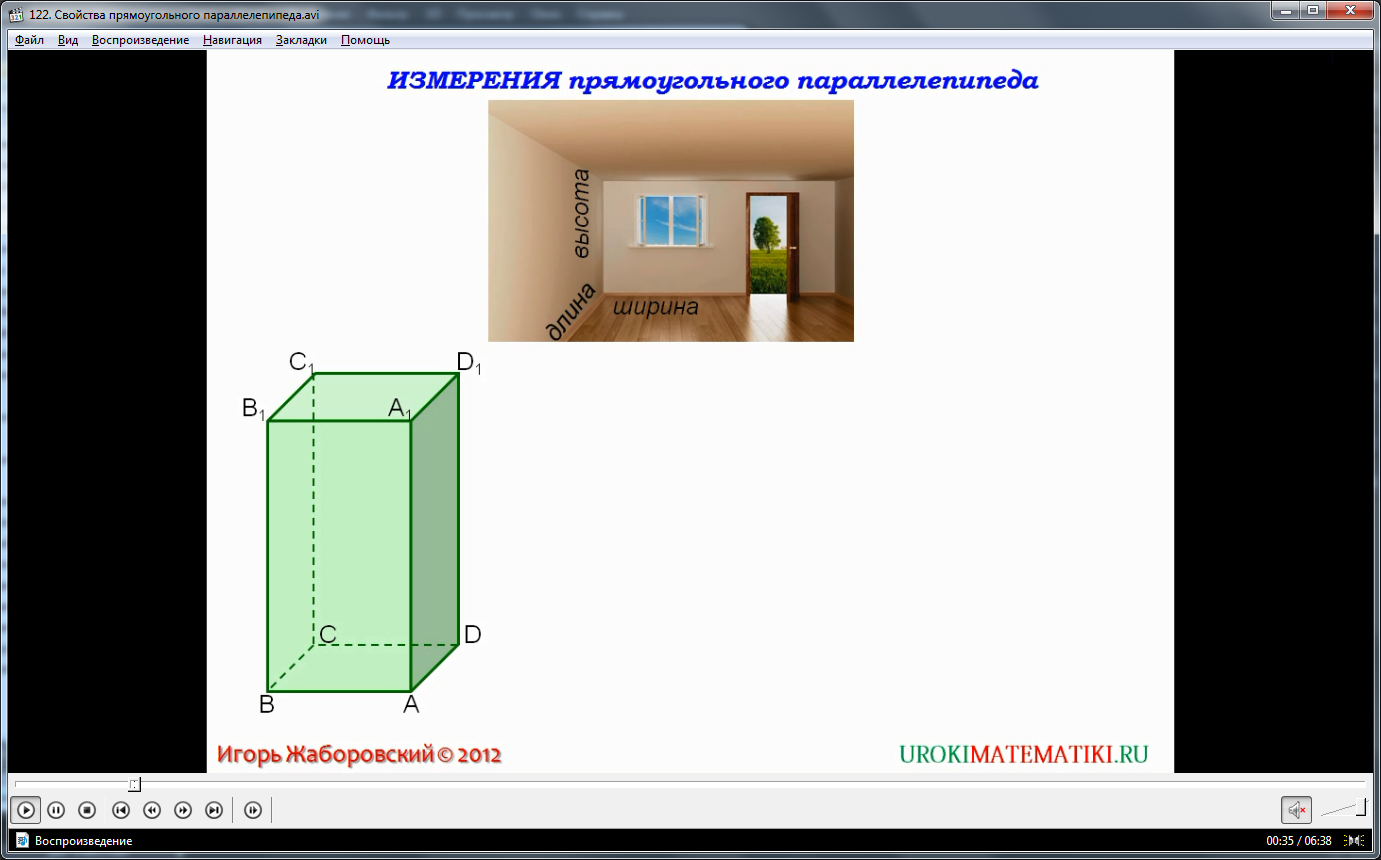
Видеоурок начинается с представления названия темы. Понятие объема прямоугольного параллелепипеда вводится с практического его отображения. На рисунке представлена комната, объем которой необходимо вычислить. Отмечается, что для этого необходимо знать ее высоту, длину, ширину. Если рассматривать комнату как геометрическую фигуру, данные измерения являются ребрами параллелепипеда, выходящими из одной вершины. В геометрии высота, ширина и длина будут называться измерениями прямоугольного параллелепипеда. Ниже на рисунке строится прямоугольный параллелепипед ABCDA1B1C1D1, в котором отмечаются ребра, длину которых необходимо знать для определения величины объема данной фигуры.

Примером таких ребер служат измерения, выходящие из вершины A – AB, AD и AA1.
Подмечается различие площади плоской фигуры, для которой достаточно знать два измерения прямоугольника – длину и ширину от прямоугольного параллелепипеда, характеризующегося тремя параметрами. Ученикам напоминается важное свойство прямоугольника, которое выражено в равенстве квадрата диагонали прямоугольника сумме квадратов его измерений – длины и ширины. Отмечено, что подобным свойством обладает и прямоугольный параллелепипед. Это свойство сформулировано на экране и выделено цветом. Оно свидетельствует о равенстве квадрата диагонали прямоугольного параллелепипеда сумме квадратов его измерений. Для доказательства данного утверждения строится прямоугольный параллелепипед ABCDA1B1C1D1. Необходимо доказать равенство AC12=АВ2+AD2+AA12. Отмечается перпендикулярность ребра CC1 плоскости ABCD, что означает перпендикулярность данного ребра любой прямой лежащей в данной плоскости, проходящей через С. Соответственно, угол ∠ACC1 является прямым. При соединении вершин А и С1 получим прямоугольный треугольник ΔАСС1. Используя теорему Пифагора, отмечаем справедливость равенства AC12=АС2+ СС12. В этом равенстве есть АС, являющаяся диагональю прямоугольника ABCD. Из данного прямоугольника выводим еще одно справедливое равенство AC2=АВ2+ AD2. При этом ребра параллелепипеда равны СС1= ВВ1= АА1. Подставив выражения из данных равенств, получаем справедливость утверждения AC12=АВ2+AD2+AA12.

Далее отмечается справедливость еще одного утверждения, выражающего похожесть свойств прямоугольника и прямоугольного параллелепипеда. Ученикам напоминается, что площадь прямоугольника вычисляется произведением его измерений. Объем прямоугольного параллелепипеда также является произведением его измерений. Формулировка утверждения выведена на экран и выделена цветом для запоминания. Для доказательства утверждения на рисунке строятся два прямоугольных параллелепипеда, лежащие одной гранью на плоскости α – параллелепипед со сторонами a, b, 1 и куб со сторонами 1. В доказательстве используется принцип Кавальери. Изображенный на рисунке куб является единицей измерения объема, так как его объем будет 1. Рисунок дополняется секущей плоскостью, площадь сечения которой куба будет равно 1, а площадь сечения параллелепипеда ab. Соответственно, площадь сечения параллелепипеда отличается от площади сечения куба в ab раз. Таким же образом отличаются и объемы описываемых геометрических тел – они отличаются в ab раз, то есть объем прямоугольного параллелепипеда с измерениями a, b, 1 будет равен V= ab. Далее рассматриваются два прямоугольных параллелепипеда, один из которых со сторонами a, b, 1, а второй сторонами a, b, с. Для демонстрации доказательства данные параллелепипеды располагаются на рисунке так, что грань ас одного параллелепипеда и грань со сторонами а и 1 второго параллелепипеда лежат на одной плоскости. Уже доказано, что объем параллелепипеда со сторонами a, b, 1 равен V= ab. Аналогично доказывается, что объем прямоугольного параллелепипеда со сторонами a, b, с будет равным abс. Отмечается, что при сечении плоскостью α площадь сечения первого параллелепипеда равна а, а второго ас. Так будет в любом сечении параллелепипеда, что означает различие объемов в с раз. Соответственно, объем второго параллелепипеда будет равен V= abс. Также данную формулу можно представить в виде произведения площади основания на высоту прямоугольного параллелепипеда. Так как площадью основания является aс, а высотой данной фигуры – b, то иначе объем параллелепипеда записывается V=Sh. Данное утверждение также представлено в текстовом виде, выведено на экран и озвучено. Также отмечено, что подобным образом определяется объем призмы. Для нее величина объема равна произведению основания призмы на ее высоту. Это утверждение также легко доказывается при помощи принципа Кавальери.

Видеоурок «Свойства прямоугольного параллелепипеда» рекомендуется использовать на уроке геометрии для повышения эффективности урока и освобождения учителя на уроке для улучшения индивидуальной работы с учениками. Также материал может быть рекомендован ученикам, требующим дополнительных занятий, для самостоятельной работы дома. Видео может стать инструментом учителя, проводящего дистанционное обучение.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 3662 |
| Номер материала | 738 |