
Урок "Связь между координатами вектора и координатами его начала и конца"

Краткое описание документа:
Видеоурок «Связь между координатами вектора и координатами его начала и конца» наглядно представляет учебный материал по данной теме. В данном видеоуроке представлены все необходимые понятия для усвоения материала, доказана связь между координатами точки и координатами ее радиус-вектора. Цели данного пособия – помочь ученикам усвоить данный материал, освободить учителя для более рационального использования времени урока. Это способствует повышению эффективности обучения.
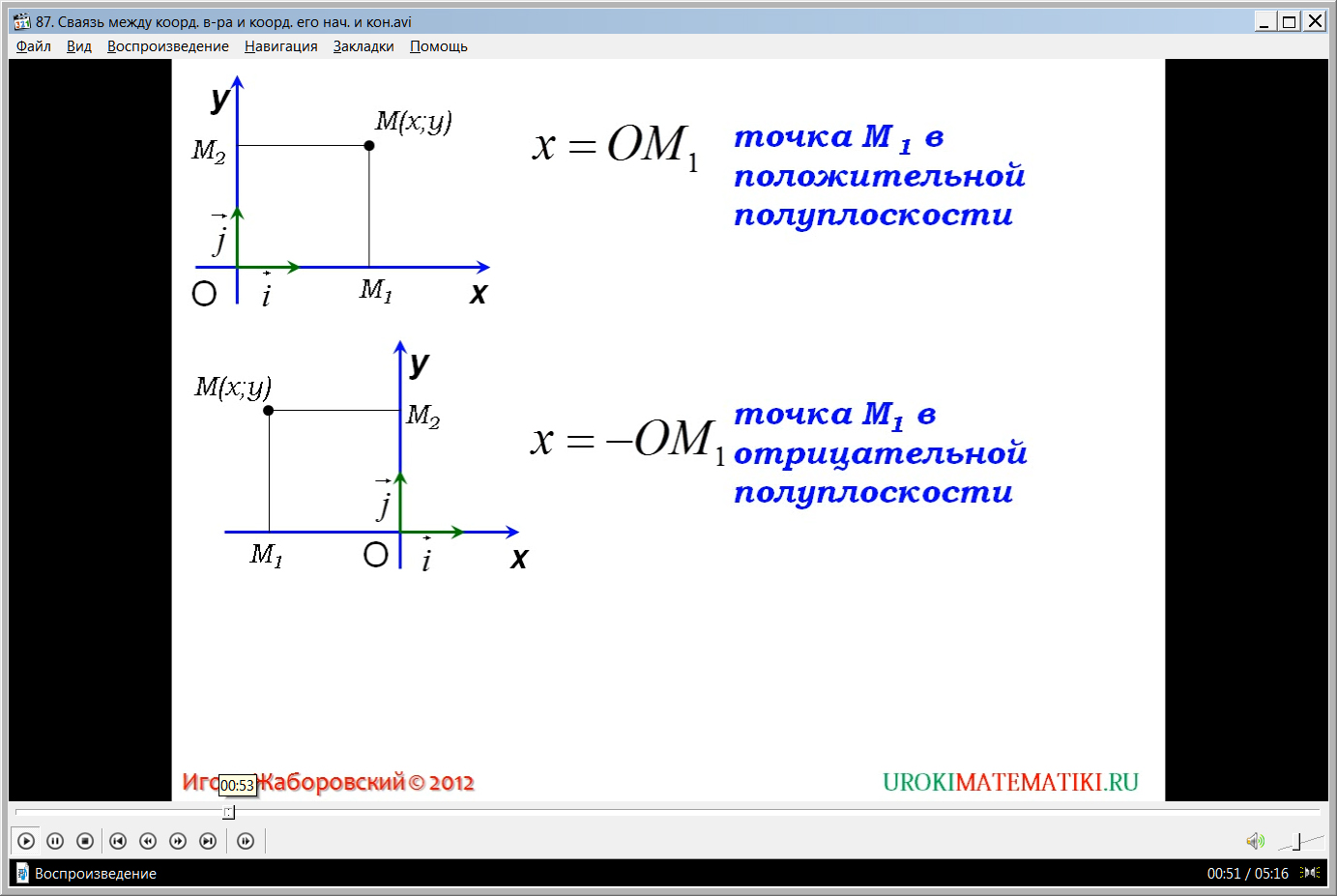
Сначала представляется тема урока. Рассмотрение темы начинается с построения прямоугольной системы координат ХОУ, на которой отмечены координатные векторы iˉ и jˉ. На координатной плоскости отмечается некоторая точка М{х;у}. Ученикам напоминается способ нахождения координат точки. Демонстрируется, как опускаются перпендикуляры на оси координат. В результате построения образуются точки пересечения перпендикуляров и оси координат М1 и М2. При этом координата х равна длине отрезка ОМ1, когда М1 располагается в положительной полуплоскости. Демонстрируется, как определяется координата точки, которая располагается в отрицательной полуплоскости. Координата х в этом случае равна длине отрезка ОМ1 со знаком минус х=-ОМ1. В случае совпадения точки пересечения перпендикуляра с началом координат О координата будет равна нулю.
Аналогично определению координат х точки определяются вторые координаты – у. На рисунке приведены примеры трех точек, которые расположены в положительной, отрицательной полуплоскости и на оси абсцисс. Для этих точек построением перпендикуляров определяются первая и вторая координата Н(-4;3), А(3;2), С(-2,5;0).
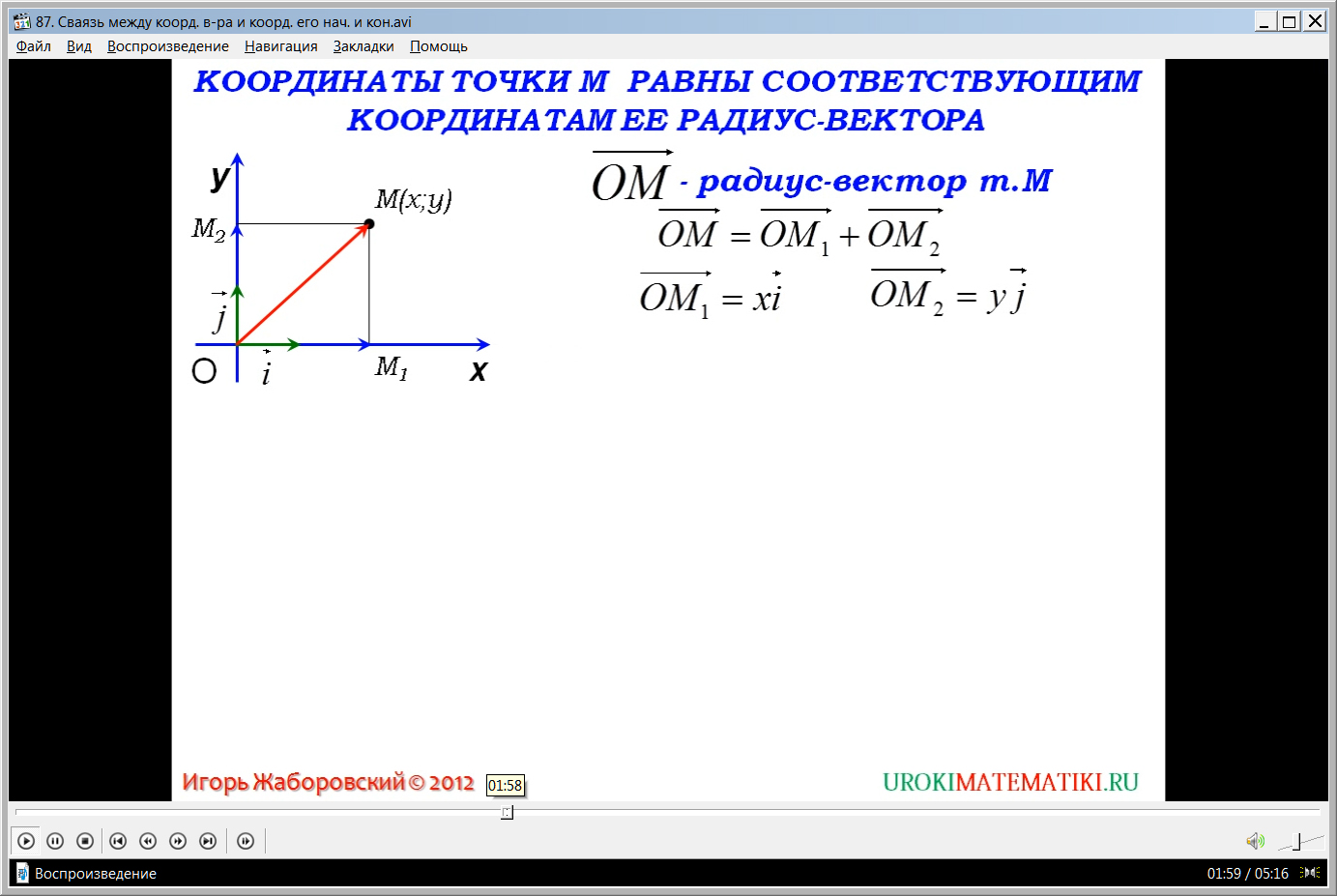
Вводится понятие радиус вектора как вектора ОМˉ, соединяющего начало координат и точку М{х;у} и направленного к точке М. Предлагается рассмотреть доказательство утверждения, что координаты точки М будут равны соответствующим координатам радиус вектора. Для доказательства используется равенство ОМˉ=ОМ1ˉ+ОМ2ˉ. Необходимо подтвердить, что ОМ1ˉ=хiˉ, а ОМ2ˉ=yjˉ. Анализируя построение, можно утверждать, что действительно в положительной полуплоскости координата х равна длине отрезка ОМ1. При этом направление вектора совпадает с направлением координатного вектора iˉ. Поэтому вектор ОМ1ˉ=ОМ1·i=хiˉ. Далее рассматривается точка, расположенная в отрицательной полуплоскости х<0. Координата х точки м равна длине отрезка ОМ1, взятой со знаком минус х=-ОМ1, так как направления координатного вектора и вектора ОМ1ˉ не совпадают. Поэтому координата радиус вектора образуется ОМ1ˉ=- ОМ·iˉ=xiˉ. Для точек, лежащих на оси ординат, ОМ1ˉ=0ˉ. Но это также соответствует выражению ОМ1ˉ=хiˉ.
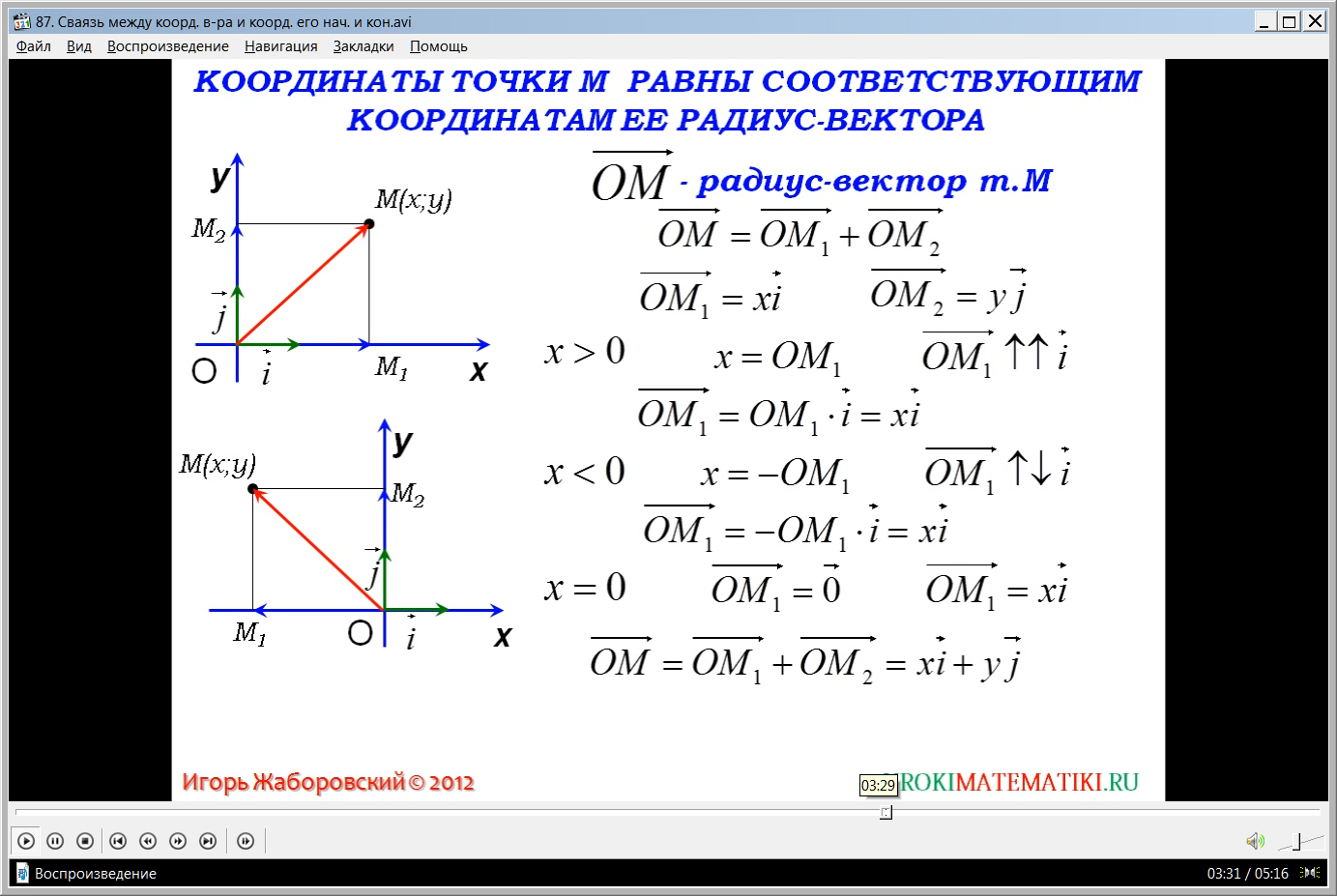
Отмечено, что таким же образом, как для выражения ОМ1ˉ=хiˉ доказывается, что вектор ОМ2ˉ=уiˉ. При этом ОМˉ= ОМ1ˉ+ ОМ2ˉ= хiˉ+ уiˉ. Значит, координаты радиус-вектора ОМˉ{х;у}. Это и необходимо было доказать.
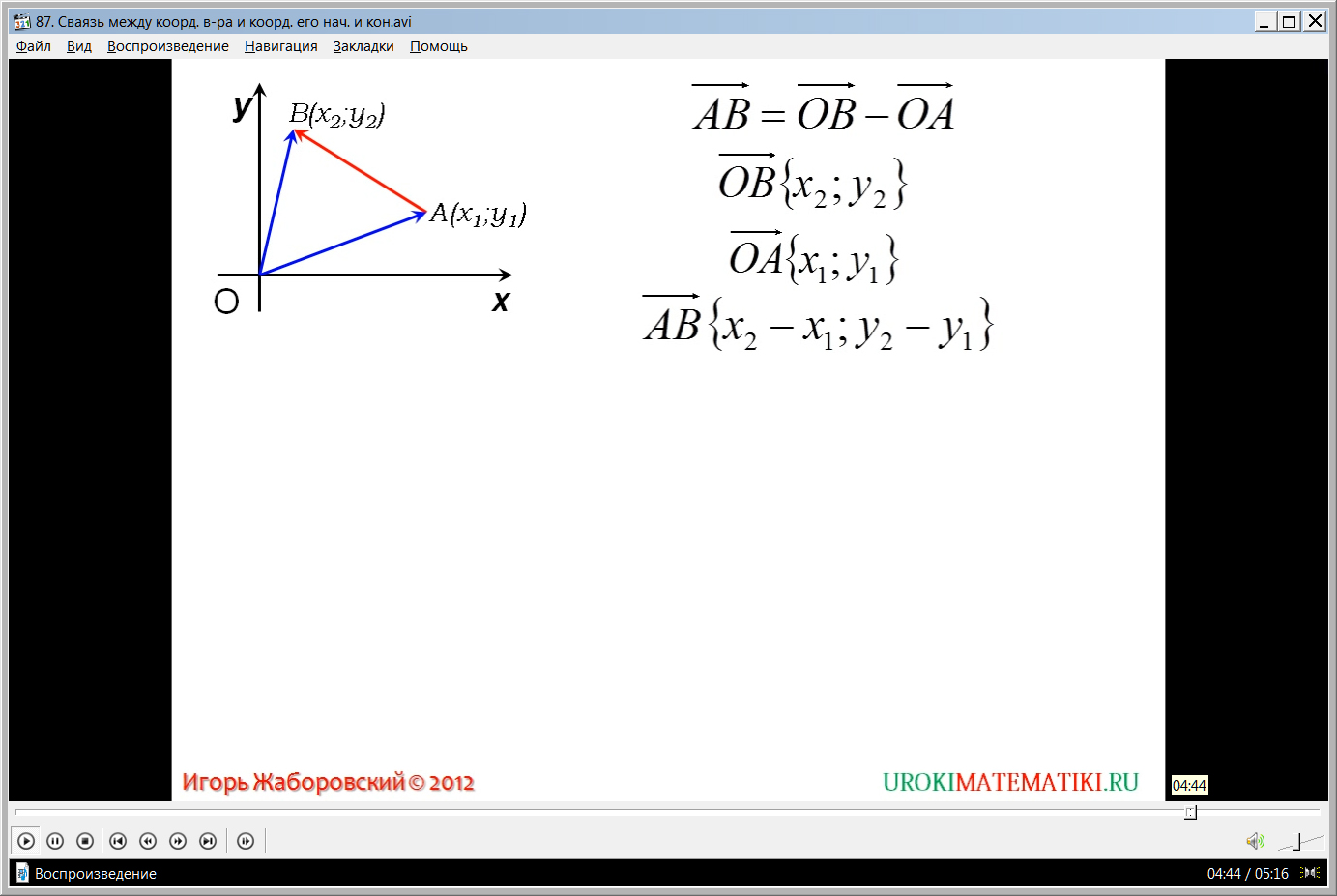
Далее, пользуясь уже доказанным утверждением, можно рассматривать координаты вектора, который образуют две произвольные точки координатной плоскости. Для этого на плоскости отмечаются две точки А{х1;у1} и В{х2;у2}, которые образуют вектор АВ ˉ. Очевидно, вектор АВˉ равен АВˉ=ОВˉ-ОАˉ, выходящим из начала координат. Однако такие векторы ОВˉ и ОАˉ являются радиус-векторами точек. Соответственно, их координаты будут ОВˉ{х2;у2}, ОАˉ{х1;у1}. При этом разность этих векторов имеет координаты АВ ˉ{х2-х1;у2-у1}. Доказательство данного утверждения дает важный вывод, что каждая координата вектора будет равна разности соответствующих координат конца и начала. Вывод отображен на экране и выделен для запоминания.
Для усвоения материала приводится пример. На координатной плоскости строится вектор ВСˉ с координатами точек В(1;4) и С(4;2). Координаты данного вектора будут равны разности соответствующих координат ВСˉ{3;-2}.
Видеоурок «Связь между координатами вектора и координатами его начала и конца» может применяться на уроке в школе как наглядное пособие. Также видеоуроки помогают донести учебный материал в ходе дистанционного обучения. Понятное подробное объяснение поможет ученику самостоятельно освоить данную тему.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 7848 |
| Номер материала | 773 |