
Урок "Тангенс суммы и разности аргументов"

Краткое описание документа:
В курсе тригонометрии, которая охватывает большое количество уроков в 10 классе, изучаются основные четыре тригонометрических функций: синус, косинус, тангенс и котангенс. Школьники должны уметь обращаться с данными функциями, строить их графики, провести анализ каждой из функции, строить графики преобразованных функций, уметь работать с таблицей тригонометрических значений и т.д.
Также, они должны уметь обращаться и воспроизводить некоторые основные формулы тригонометрии, использовать их при решении практических примеров. Это все рассматривалось в предыдущих видеоуроках. Школьники могут просмотреть и освежить материал в своей голове.
Итак, данный видеоурок посвящен изучению формул тангенса суммы и разности аргументов. Ранее изучались формулы синуса суммы и разности аргументов, также косинуса.
Они демонстрируются диктором и выводятся на экран, 0обведенные в красные рамки, для того, чтобы подчеркнуть важность запоминания данных формул.
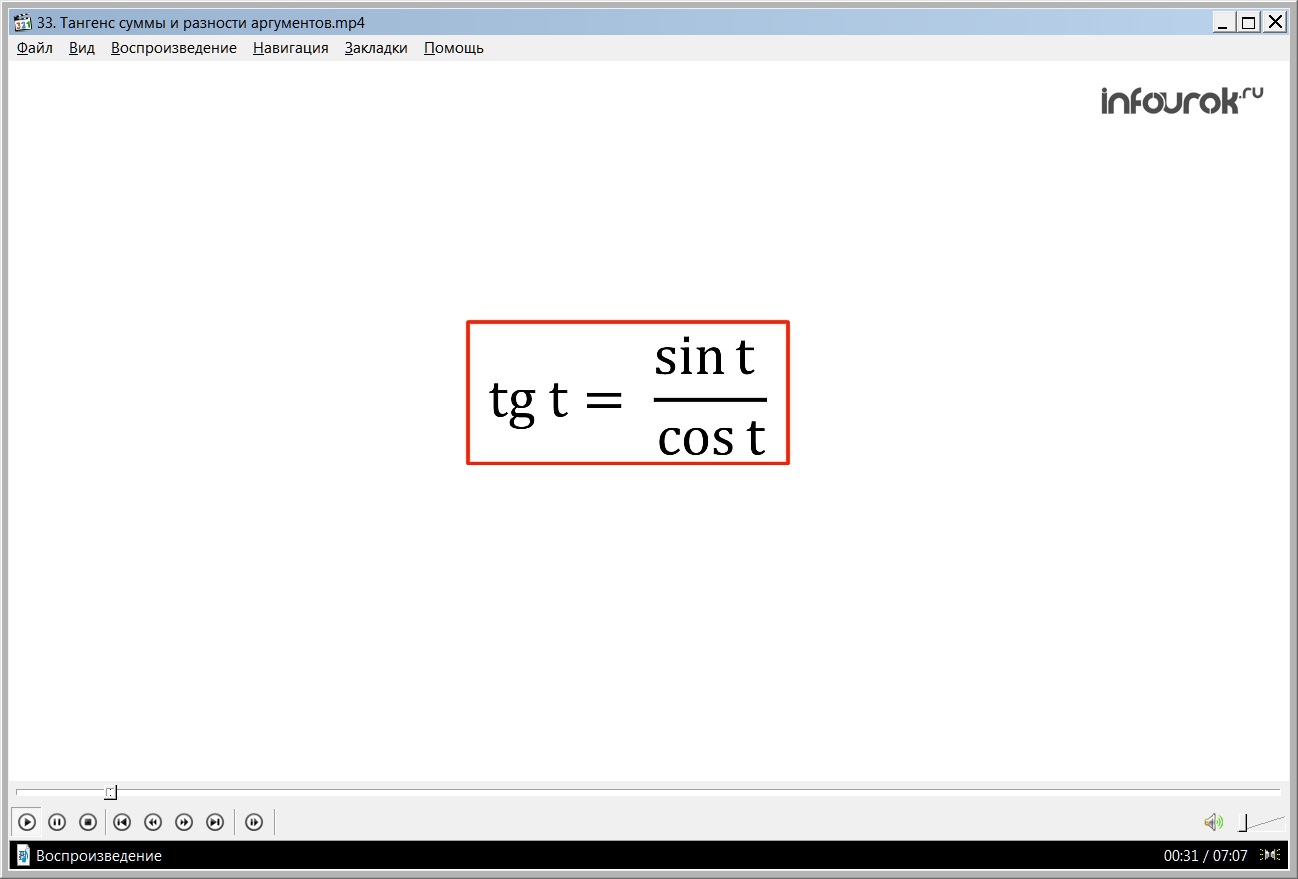
Что касается тангенса, мы знаем, как можно записать данное понятие, то есть выразить, через синус и косинус. Тангенс суммы аргументов можно записать как деление синуса суммы аргументов на косинус суммы аргументов. Имеем дробь, где числитель и знаменатель можно расписать по изученным заранее формулам. Получаем уже готовую новую формулу, которую можно слега упростить и преобразовать. Диктор предлагает каждый член многочлена поделить на произведение косинуса одного аргумента и синуса иного. Поделив, некоторые члены сократятся, и выражение уменьшится в целом.
Получаем упрощенную новую формулу, которую стоит запомнить. Если понять принцип ее получения, то никаких проблем в дальнейшем понимании и запоминании не появятся.
Далее указывается, что аргументы не могут принимать значения, которые лежат на асимптотах графика функции тангенса. Для сумм аргументов также выводятся исключения. Этот момент учитель обязательно должен рассмотреть с классом.
В первом примере, который выводится в видеоуроке, предлагается вычислить некоторое достаточно большое дробное вырадение, которое и в знаменателе, и в числителе содержит сумму тангенсов. Так как аргументы при тангенсе не являются табличными значениями, рекомендуется привести их в виде суммы более удобных градусов. Проделав данную процедуру можно использовать изученную формулу для дальнейшего решения и получения ответа.
Второй пример предлагает упростить некоторое выражение, которое представляет собой сумму двух дробей. С правой стороны приводятся все выноски, которые используются при решении задачи. Диктор спокойным и понятным голосом объясняет все шаг за шагом. Не пропущен ни один момент.
Третий пример более сложный. Здесь предлагается вычислить тангенс от некоторого значения, если известны некоторые данные. При решении также пользуются ранее изученные формулы, которые появляются в выносках с правой стороны.
Решение достаточное длинное. Выводится в итоге ответ. После этого примера, в видеозаписи рассматривается еще один пример-уравнение. Так как при его решении и используется тригонометрическая таблица значений, она выводится на экран для наглядности и простоты. Таким образом, школьники могут увидеть, откуда взяты те или иные значения, лучше понять.
Подобные примеры можно задать ученикам для выполнения дома. Если у них появятся проблемы при решении, они могу т обратиться к данной видеозаписи и просмотреть еще раз.
Данный электронный ресурс может быть использован для демонстрации в школе во время урока. Учитель сможет «оживить» урок с помощью подобных материалов. Он станет более запоминающимся и интересным. В случае если у школьников появятся вопросы, учитель или репетитор, просматривающий вместе с ним урок, сможет прокомментировать более подробно и объяснить. Сообразительные ученики смогут самостоятельно понять материал и освоить без дополнительной помощи.
ТЕКСТОВАЯ РАСШИФРОВКА:
Тангенс суммы и разности аргументов
Мы уже познакомились с формулами, которые выражают синус и косинус суммы и разности аргументов. Показать формулы
Рассмотрим, как можно выразить тангенс суммы и разности аргументов. Вспомним, что тангенс, это отношение синуса числа к косинусу этого числа
Тогда тангенс суммы двух углов выразим через синус и косинус суммы двух углов, применяя формулы синус суммы и косинус суммы:
sin(x + y) = sin x cos y + cos x sin y,
cos (x + y) = cos x cos y - sin x sin y.
tg(х+у)
Далее разделим числитель и знаменатель дроби на произведение cosxcosy
(ведь, если существуют тангенсы углов х и у, произведение косинусов этих углов отлично от нуля), после деления числителя и знаменателя на cosxcosy получим в числителе сумму а это равно tgx и а это равно tgy.
В знаменателе сокращаем и получаем единицу
как и в числителе а это равно tgxи а это равно tgy.
Следовательно, tg(x+y) =.
( Тангенс суммы двух аргументов равен сумме тангенсов этих аргументов, деленной на единицу минус произведение тангенсов этих аргументов.)
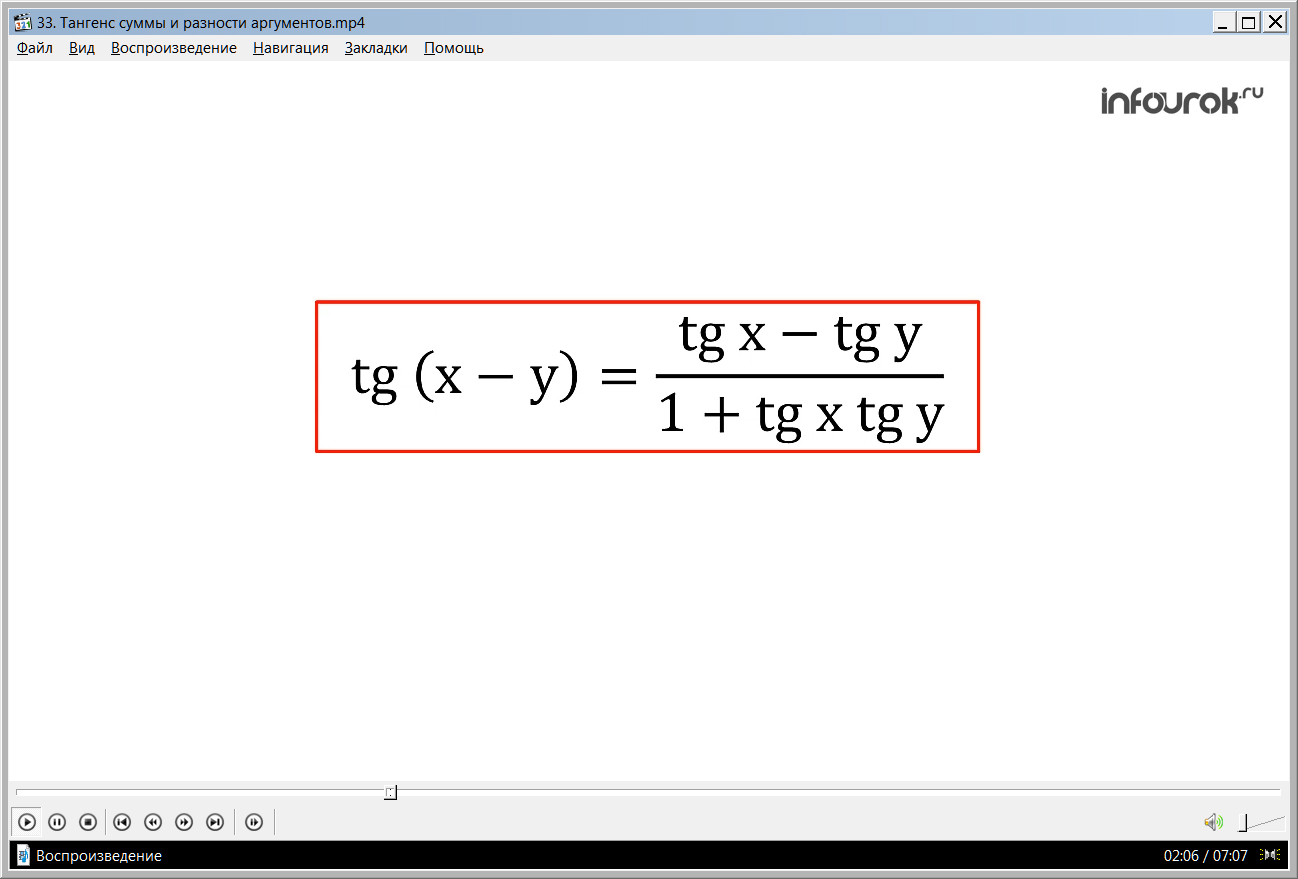
Аналогично доказывается формула для тангенса разности аргументов:
tg(х–у) =. ( Тангенс разности двух аргументов равен разности тангенсов этих аргументов, деленной на единицу плюс произведение тангенсов этих аргументов.)
Разумеется, что все тангенсы имеют смысл, т.е. х+ πn, у + πn,
х+у+ πn (для тангенса суммы двух аргументов), х – у+ πn (для тангенса разности двух аргументов).
Рассмотрим примеры.
ПРИМЕР 1. Вычислить .
Решение. Данное выражение представляет собой правую часть формулы тангенс суммы для аргументов 16° и 44°. Следовательно, приведем выражение к виду левой части и получим, что тангенс равен 600 , следовательно равен . (Показать таблицу значений)
= tg(16°+44°) = tg 60° = .
Ответ: .
ПРИМЕР 2. Упростить выражение + (частное суммы тангенсов аргументов икс и игрек на тангенс суммы этих аргументов плюс частное разности тангенсов аргументов икс и игрек на тангенс разности этих аргументов).
Решение. В знаменателе первой и второй дроби применим формулы тангенса суммы и разности аргументов, проведем сокращения и получим 1 – tgxtgy + 1 + tgxtgy , – tgxtgy и tgxtgy в результате дает ноль, тогда в ответе 2.
+ = + = 1 – tgxtgy + 1 + tgxtgy = 2.
Ответ: 2.
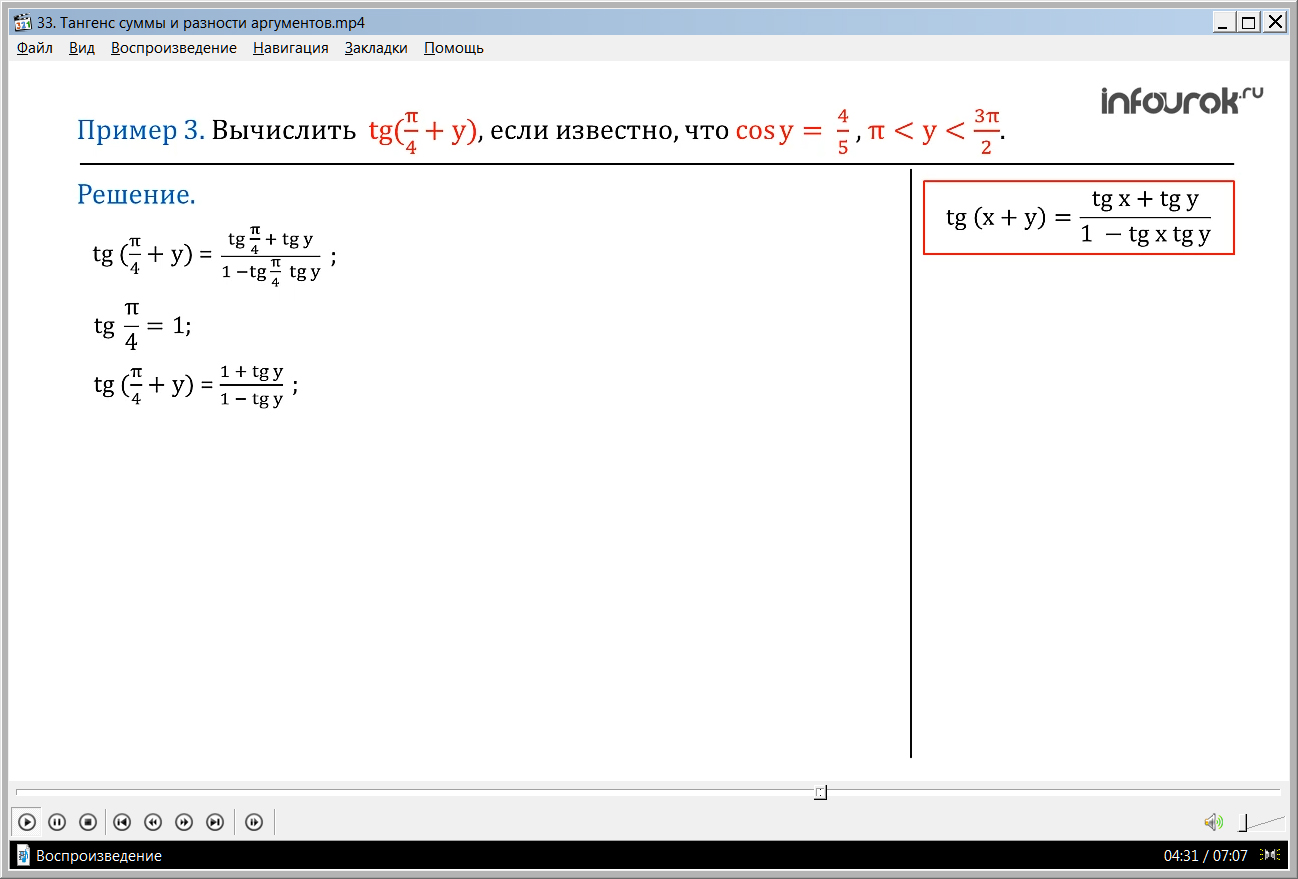
ПРИМЕР 3. Вычислить tg(+y) (тангенс пи на четыре плюс игрек), если известно, что cosy = , π <у< ( игрек больше пи, но меньше трех пи на два).
Решение. Применяя формулы тангенса суммы аргументов, получим
Найдем tgy (зная, cosy = , π<у<), воспользовавшись формулой . Получим tg2у = – 1 подставим значение косинуса в формулу, тогда получим – 1 = .
tg2у = – 1 – 1 = .
tg2 у =. Извлечем корень квадратный tg у = и tg у =
По условию аргумент у (игрек) принадлежит третьей четверти, а там тангенс положительный. Значит, tg у = . А сейчас вернемся к первоначальной формуле и подставим найденное значение:
= = = 7.
Ответ: = 7.
ПРИМЕР 4. Решить уравнение =–1 (Разность тангенсов трех икс и икс, деленная на сумму единицы и произведения тангенсов трех икс и икс равно минус единице).
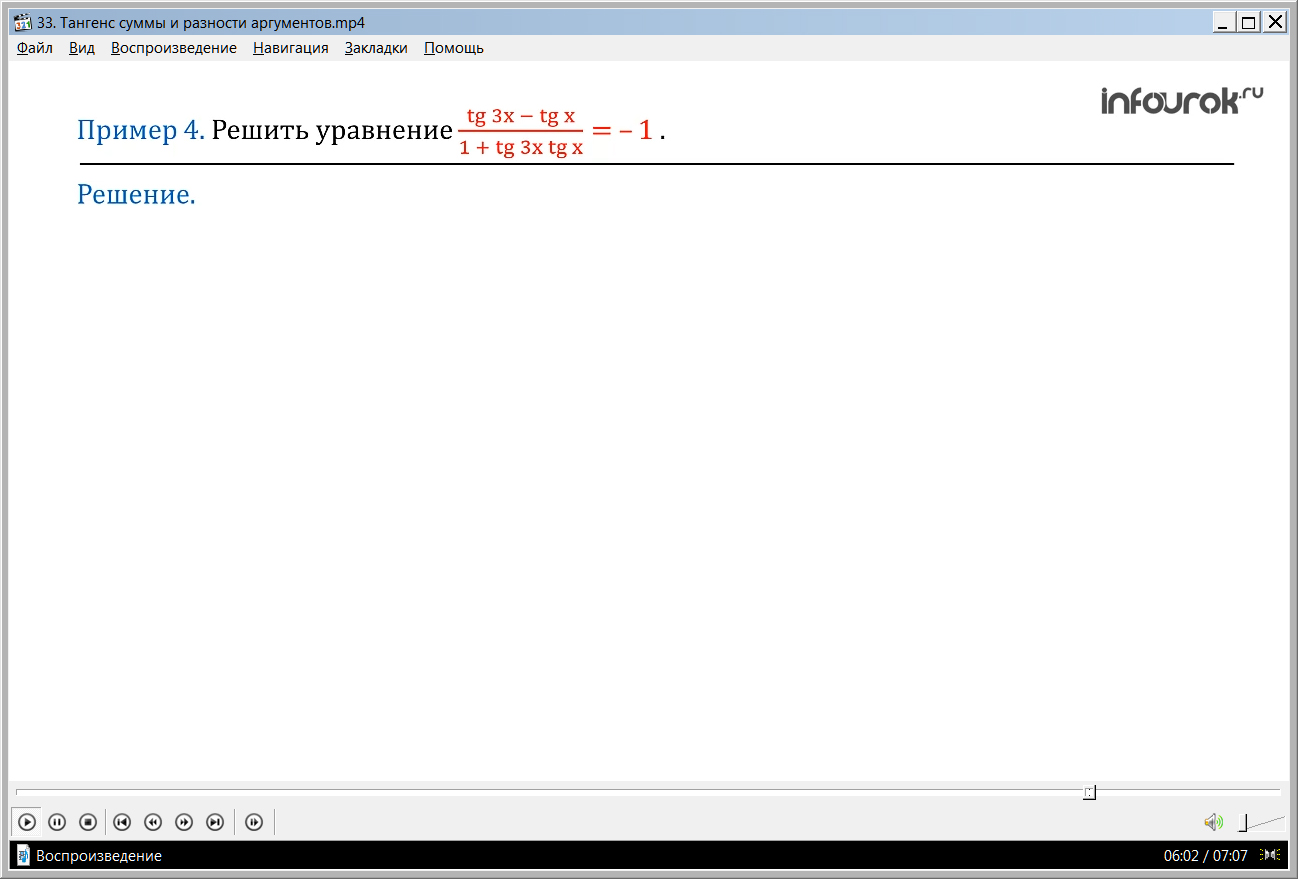
Решение. Заметим в левой части уравнения формулу тангенса разности аргументов три икс и икс. Имеем
= –1,
tg(3x–x) =– 1, от получим 2х, значит
tg2x = – 1,
2х = arctg (-1) + πn, (два икс равно арктангенс минус единицы плюс пи эн).
Так как arctg (-1)= –arctg 1, тогда tg (-1) = Показать таблицу
Подставляем данные в выражение и получаем:
2х =–+ πn, (два икс равно минус пи на четыре плюс пи эн)
x = –+, ( икс равно минус пи на восемь плюс пи эн, деленное на два)
Ответ: x = –+,.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 9686 |
| Номер материала | 846 |