
Урок "Теорема, обратная теореме Пифагора"

Краткое описание документа:
Рассмотрение тем школьной программы с помощью видеоуроков является удобным способом изучения и усвоения материала. Видео помогает сконцентрировать внимание учащихся на основных теоретических положениях и не упускать важных деталей. При необходимости школьники всегда могут прослушать видеоурок повторно или вернуться на несколько тем назад.

Данный видеоурок для 8-го класса поможет учащимся изучить новую тему по геометрии.
В предыдущей теме мы изучили теорему Пифагора и разобрали ее доказательство.
Существует также теорема, которая известна как обратная теорема Пифагора. Рассмотрим ее подробнее.
Теорема. Треугольник является прямоугольным, если в нем выполняется равенство: значение одной стороны треугольника, возведенной в квадрат, такое же, как сумма возведенных в квадрат двух других сторон.

Доказательство. Допустим, нам дан треугольник ABC, в котором выполняется равенство AB2 = CA2 + CB2. Необходимо доказать, что угол С равен 90 градусов. Рассмотрим треугольник A1B1C1, в котором угол С1 равен 90 градусов, сторона C1 A1 равна CA и сторона B1C1равна BС.
Применяя теорему Пифагора, запишем отношение сторон в треугольнике A1C1B1: A1B12 = C1A12 + C1B12. Произведя замену в выражении на равные стороны, получим A1B12 = CA2 + CB2.
Из условий теоремы мы знаем, что AB2 = CA2 + CB2. Тогда можем записать A1B12 = AB2, из чего следует, что A1B1= AB.
Мы нашли, что в треугольниках ABC и A1B1C1равны три стороны: A1C1 = AC, B1C1 = BC, A1B1= AB. Значит, эти треугольники равны. Из равенства треугольников следует, что угол С равен углу С1 и соответственно равен 90 градусов. Мы определили, что треугольник ABC прямоугольный и его угол С равен 90 градусов. Мы доказали данную теорему.

Далее автор приводит пример. Допустим, дан произвольный треугольник. Известны размеры его сторон: 5, 4 и 3 единиц. Проверим утверждение из теоремы, обратной теореме Пифагора: 52 = 32 + 42. Утверждение верно, значит данный треугольник прямоугольный.
В следующих примерах треугольники также будут прямоугольными, если их стороны равны:
– 5, 12, 13 единиц; равенство 132 = 52 + 122 является верным;
– 8, 15, 17 единиц; равенство 172 = 82 + 152 является верным;
– 7, 24, 25 единиц; равенство 252 = 72 + 242 является верным.
Известно понятие пифагорового треугольника. Это прямоугольный треугольник, у которого значения сторон равны целым числам. Если катеты пифагорового треугольника обозначить через a и c, а гипотенузу b, то значения сторон этого треугольника можно записать с помощью следующих формул:
a = 2k x m x n
b = k x (m2 – n2)
c = k x (m2 + n2)
где m, n, k– любые натуральные числа, причем значение m больше значения n.
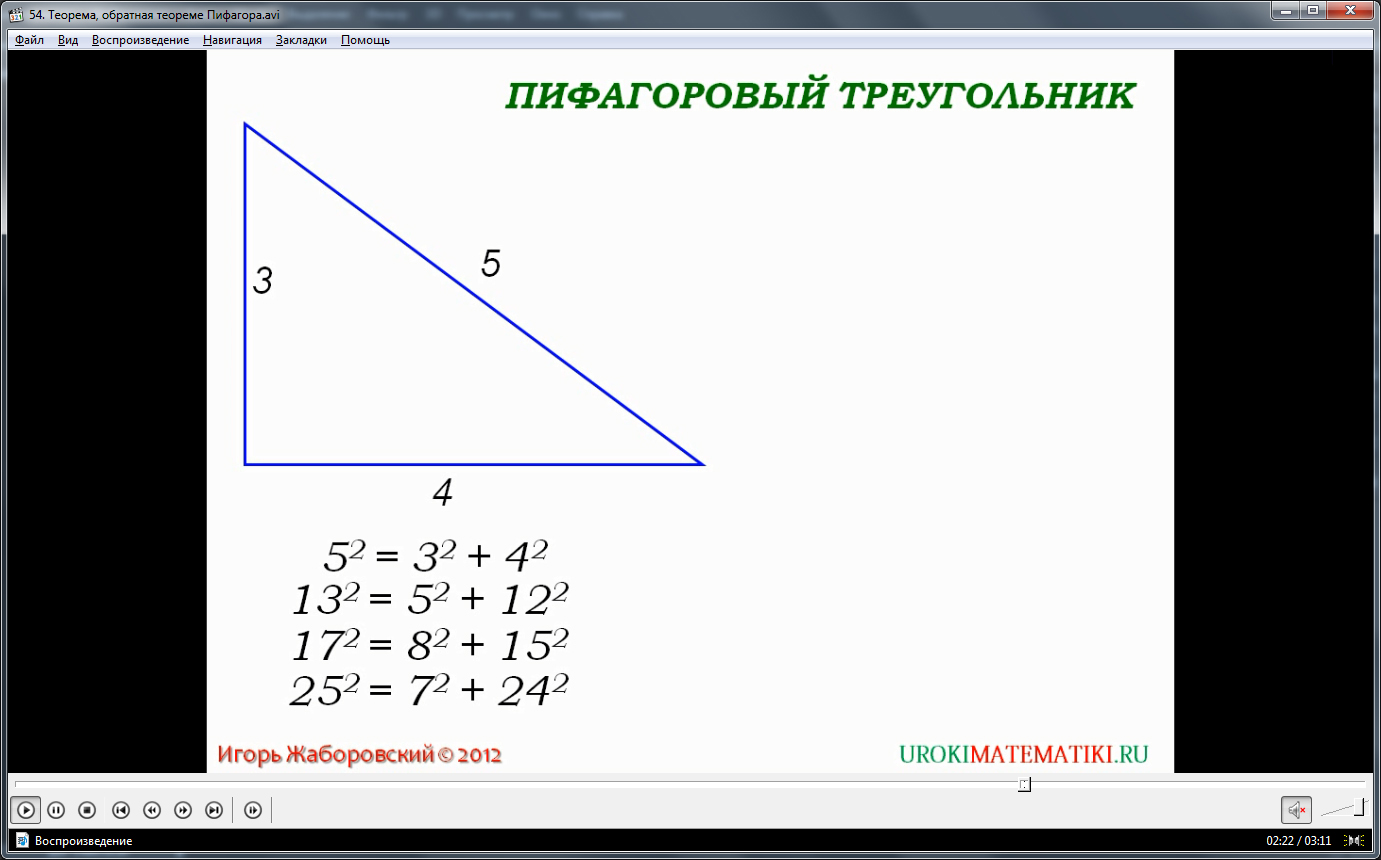
Интересный факт: треугольник со сторонами 5, 4 и 3 называют также египетским треугольником, такой треугольник был известен еще в Древнем Египте.
В данном видеоуроке мы ознакомились с теоремой, обратной теореме Пифагора. Подробно рассмотрели доказательство. Также учащиеся узнали, какие треугольники называют пифагоровыми.
Видеоматериалы, представленные автором, могут быть применены учителем при проведении урока геометрии, так как последовательно и наглядно демонстрируют все положения изучаемой темы.
Учащиеся с легкостью могут ознакомиться с темой «Теорема, обратная теореме Пифагора» самостоятельно с помощью данного видеоурока.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 9037 |
| Номер материала | 592 |