
Урок "Тригонометрические уравнения"

Краткое описание документа:
Несколько уроков назад учащиеся уже начали изучать тригонометрические уравнения, рассмотрели разнообразные примеры.
В данной теме перейдем к их более углубленному изучению. В начале урока дается определение тригонометрического уравнения, указывается, какие уравнения относятся к простейшим тригонометрическим уравнениям:
sin (kx + m) = a
cos (kx + m) = a
tg (kx + m) = a
ctg (kx + m) = a
Приводятся решения уравнений, которые были изучены ранее:
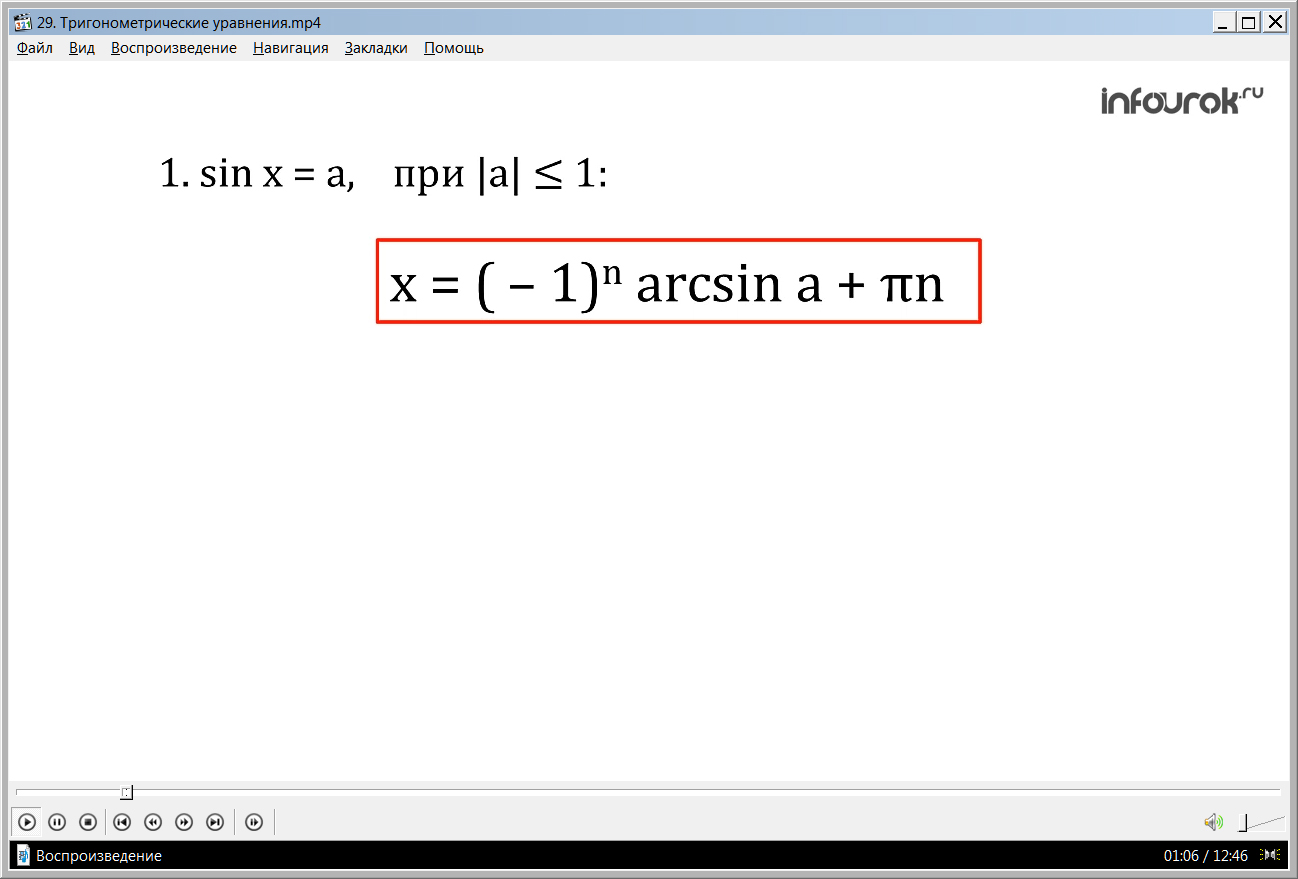
1) sin x = a, если модуль а меньше или равен единице, х = (– 1)narcsin a + πn. Или: х = arcsin a + 2πk; х = π – arcsin a+ 2πk;
2) cos x = a, когда модуль а меньше или равен единице, x = ± arccos a + 2πn;
3) если модуль а больше единицы, то уравнения sin x = a и cos x = a не имеют решений;
4) tg x = a имеет решение для любого значения а, х = arctg а + πn;
5) ctg x = a имеет решение для любого значения а, х = arcctg а + πn;
6) в пункте отражены частные случаи решения уравнений sin x = a и cos x = a при а = 0, а = 1 и а = – 1, которые для наглядности представлены в таблице.
Далее рассмотрим примеры решений. Пример 1: решить уравнение, содержащее sin.
Для решения вводится новая переменная t, которая равна значению переменной под знаком sin, в данном случае t = 4x. Запишем исходное выражение, заменяя x на t. Определим, что модуль а меньше либо равен единице, а значит уравнение имеет решение вида х = (– 1)narcsin a + πn. Напишем это выражение с помощью переменной t. По таблице значений найдем решение arcsin, зная которое, запишем значение t. Далее, подставив вместо t 4x, найдем ответ: х = (– 1)nπ/16 + πn/4. Кстати, новую переменную можно не вводить и решать уравнение только с х; в нашем случае мы ввели новую переменную для удобства решения.
Пример 2. Найти такие решения уравнения, которые принадлежат интервалу от 0 до π/2. Дано такое же уравнение, как в примере 1. Из примера 1 выпишем х = (– 1)nπ/16 + πn/4. Далее, подставляя вместо n целые числа, получим:
1) при n = 0: х = π/16; этот корень решения принадлежит промежутку от 0 до π/2;
2) при n = 1: х = 3π/16; это значение принадлежит отрезку от 0 до π/2;
3) при n = 2: х = 9π/16; это число не принадлежит интервалу от 0 до π/2, а также не будут принадлежать данному интервалу другие значения х при n > 2;
4) при n = – 1: х = – 5π/16; это значение не принадлежит промежутку от 0 до π/2, а также не будут принадлежать данному промежутку другие значения х при n < – 1.
Итак, мы можем сделать вывод, что решениями заданного уравнения, принадлежащими интервалу от 0 до π/2, будут такие значения х, которые получаются при n = 0 и при n = 1: π/16 и 3π/16.
Перейдем к примеру 3. Решить уравнение, содержащее tg и ctg. Введем новую переменную y. Тогда исходное уравнение примет вид y + 1/y = 3, корнями которого будут у = 1 и у = 2. Используя формулу решения х = arctg а + πn и подставляя значения найденных у в исходное уравнение, найдем: x = 3π/4 + 3πn и x = 3 arctg2 + 3πn.
Рассмотрим еще такое уравнение 2 cos x sin 7x – sin 7x = 0 (пример 4).Используя метод разложения на множители, переходим к решению двух уравнений: sin 7x = 0 и 2 cos x – 1 = 0.
Применяем формулу решения cos x = a при модуле а меньше или равном единице: x = ± arccos a + 2πn, в данном примере х = ± arccos 0,5 + 2πn. Найдем, что arccos 0,5 = π/3. Подставим это значение и получим х = ± π/3 + 2πn.
В примере 4 мы произвели переход от уравнения f1 (х) * f2 (х) = 0. Автор делает акцент на том, что при таком переходе необходимо быть внимательным. Для примера рассмотрим задачу 5 – решить уравнение ctq x (cos x – 1) = 0. При решении переходим к решению двух уравнений ctq x = 0 и cos x – 1 = 0. Корень первого уравнения х = π/2 + πn, а второго х = 2πn. Но корень х = 2πn включить в решение исходного уравнения мы не можем, т.к. ctq x не будет иметь смысла. Корень х = 2πn называется посторонним корнем, т.к. не принадлежит области определения уравнения. Тогда ответ данного уравнения будет выглядеть как х = π/2 + πn.
ТЕКСТОВАЯ РАСШИФРОВКА:
Тригонометрические уравнения
Уравнения, в которых переменная содержится под знаком тригонометрических функции, называются тригонометрическими.
Познакомимся с простейшими тригонометрическими уравнениями. К простейшим тригонометрическим уравнениям относят уравнения вида sin(kx +m)=a, cos(kx +m)=a, tg(kx +m)=a, ctg(kx +m)=a.
Мы уже изучили, что
- Решения уравнения sinx=a, при | а | 1, имеют вид:
х = ( - 1)n arcsin a + πn.
или эти решения можно записать по-другому
х = arcsin a + 2πk, х = π - arcsin a + 2πk.
- Решения уравнения cosx=a, при | а | 1, имеют вид:
х = arccos a + 2πn.
- Если | а | 1, то уравнения sinx=a и cosx=a не имеют решений.
- Уравнение tg x = a имеет решение для любого значения а и эти решения имеют вид х = arctg x a + πn.
- Уравнение ctg х = a имеет решение для любого значения а и эти решения имеют вид: х = arcсtg а + πn.
- Важно помнить частные случаи:
Во всех формулах подразумевается, что nϵZ, kϵZ( эн и ка принимают любые целочисленные значения).
Рассмотрим примеры.
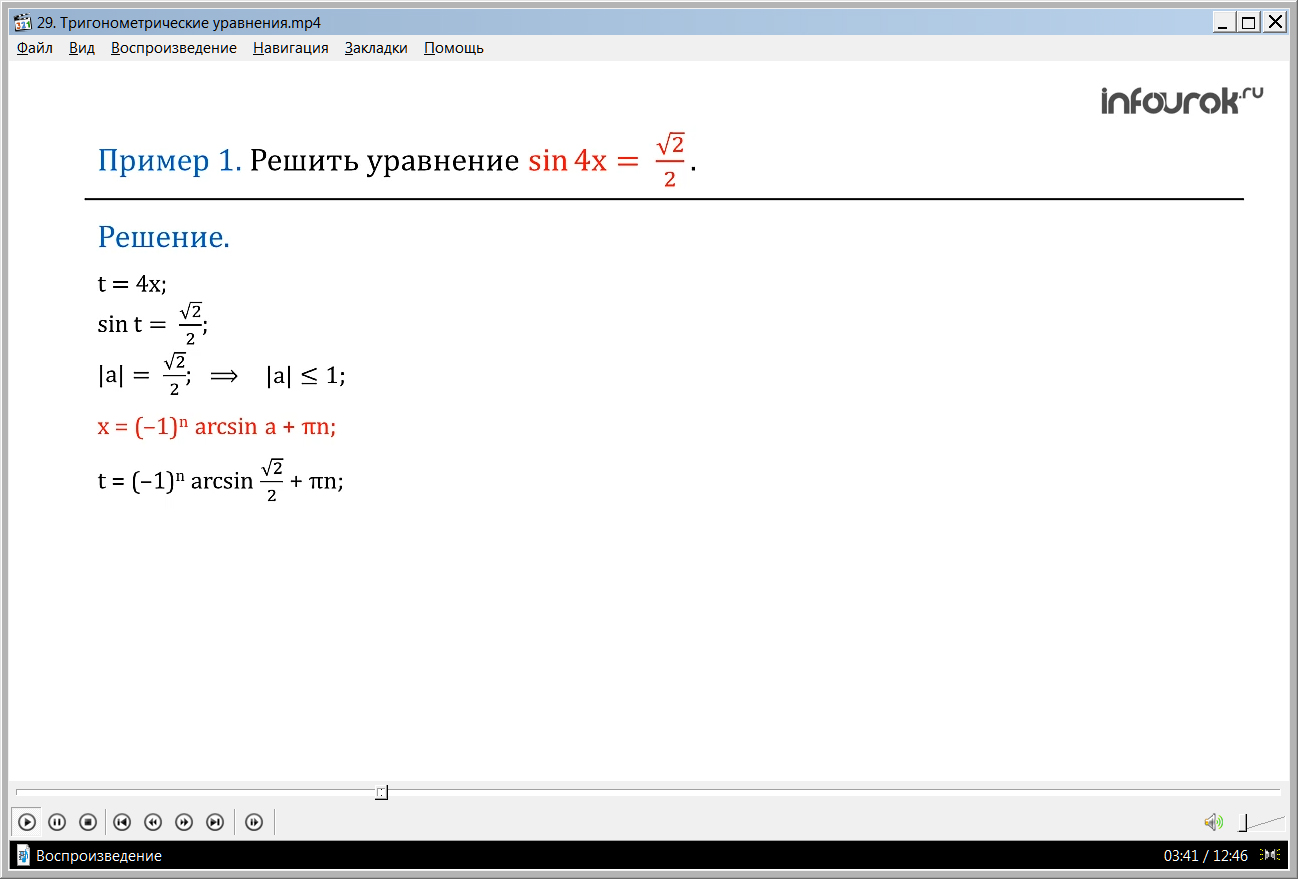
ПРИМЕР 1. Решить уравнение sin 4x= .
Решение. Введем новую переменную t = 4x, получим sin t = . Так как |а|= , значит | а | 1 и решение уравнения имеет вид х = (–1)narcsina + πn.
Тогда t =(–1)narcsin +πn ( тэ равно минус единица в степени эн умноженная на арксинус корня из двух на два плюс пи эн). А так как arcsin = , то
t = (–1)n+πn .Следовательно, 4х = (1)n+πn. Разделим обе части на четыре, получим х = (- 1)n+.(произведение минус единицы в степени эн и пи, деленного на шестнадцать плюс пи эн на четыре).
ЗАМЕЧАНИЕ. Необязательно вводить новую переменную. Можно сразу от уравнения sin 4x= переходить к уравнению 4х = (–1)n + πn.
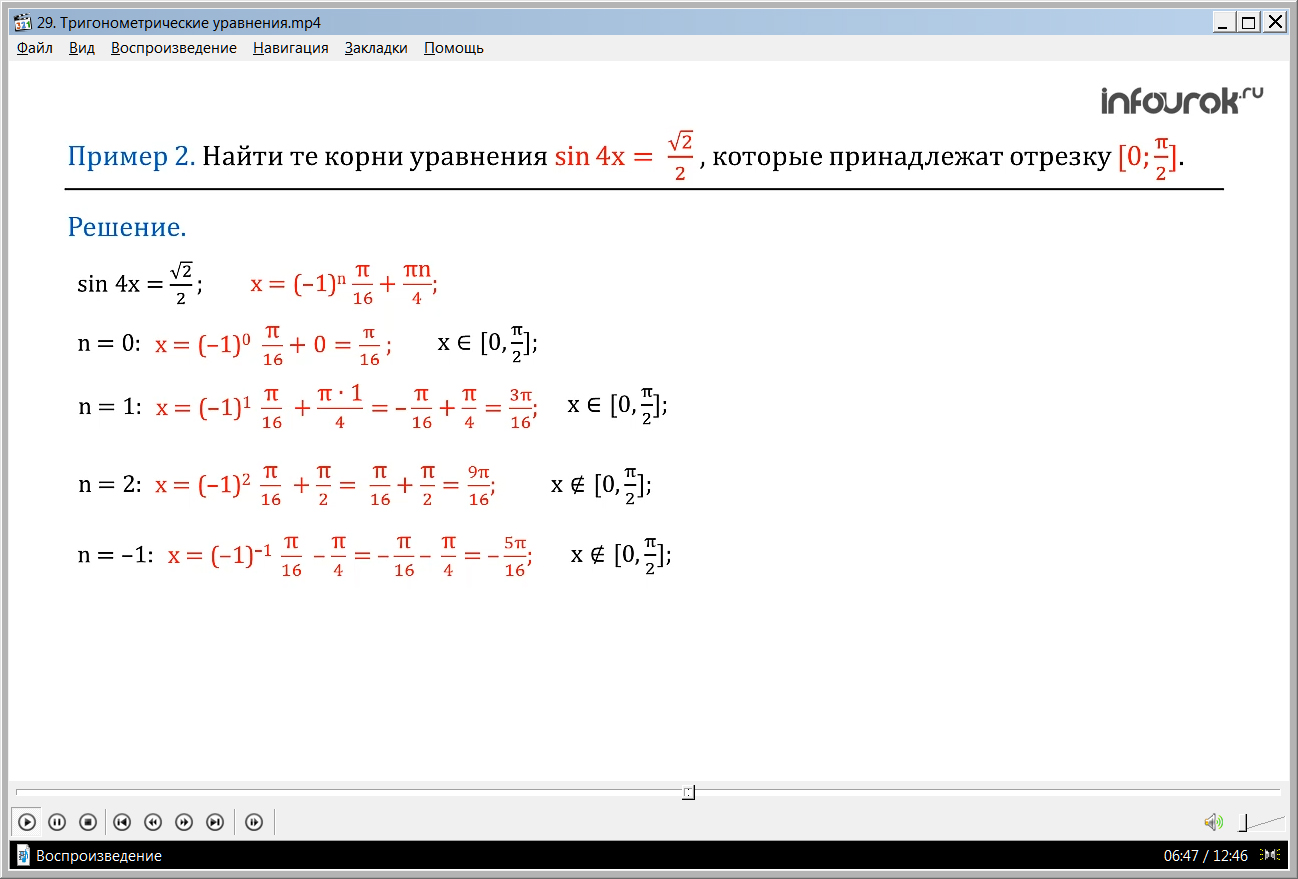
ПРИМЕР 2. Найти те корни уравнения sin 4x= , которые принадлежат отрезку [0, ].
Решение. Как мы знаем из примера 1, решение уравнения sin 4x= записано в виде х=(–1)n+. Далее, придавая параметру n целочисленные значения и подставляя эти значения в общую формулу корней, получим
1) если n=0, х = (- 1)0 +0 = . Это число принадлежит заданному отрезку [0, ].
2) если n =1, х=(–1)1+== – + = . Это число принадлежит заданному отрезку [0, ].
3) если n =2, х =(- 1)2 + = + = . Это число не принадлежит заданному отрезку [0, ]. Тем более не будут принадлежать заданному отрезку значения икс, которые получаются из общей формулы при n 2.
4) рассмотрим n = - 1, х =(- 1)- 1 - = – – = . Это число не принадлежит заданному отрезку [0, ], так как отрицательное. Тем более не будут принадлежать заданному отрезку значения икс, которые получаются из общей формулы при n<–1.
Итак, заданному отрезку [0, ] принадлежат те корни уравнения, которые получаются из общей формулы при n=0 и n =1. Эти корни и .
Ответ: , .
Для решения тригонометрических уравнений чаще всего используют метод введения переменной или метод разложения на множители.
ПРИМЕР 3. Решим уравнение tg + 2 сtg = 3 ( сумма тангенса икс на три и удвоенного котангенса икс на три равно трем).
Решение. Используем метод введения переменной. Пусть у = tg , тогда
сtg = (так как tgt ∙ сtgt = 1). Получим уравнение у + = 3, которое приведем к квадратному у2 – 3у + 2 = 0. Корни этого уравнения 1 и 2.
Вернемся к переменной икс и получим два уравнения tg = 1 или tg = 2.
Так как уравнение tg x = a имеет решение для любого значения а и эти решения имеют вид х = arctg x a + πn, то для первого уравнения имеем: = arctg 1 + πn = + πn , значит, х = + 3πn(три пи на четыре плюс три пи эн).
Для второго уравнения имеем: =arctg2+πn , значит, х=3arctg2+3πn(сумма трех арктангенсов двух и трех пи эн).
Ответ: х = + 3πn, 3arctg2+3πn.
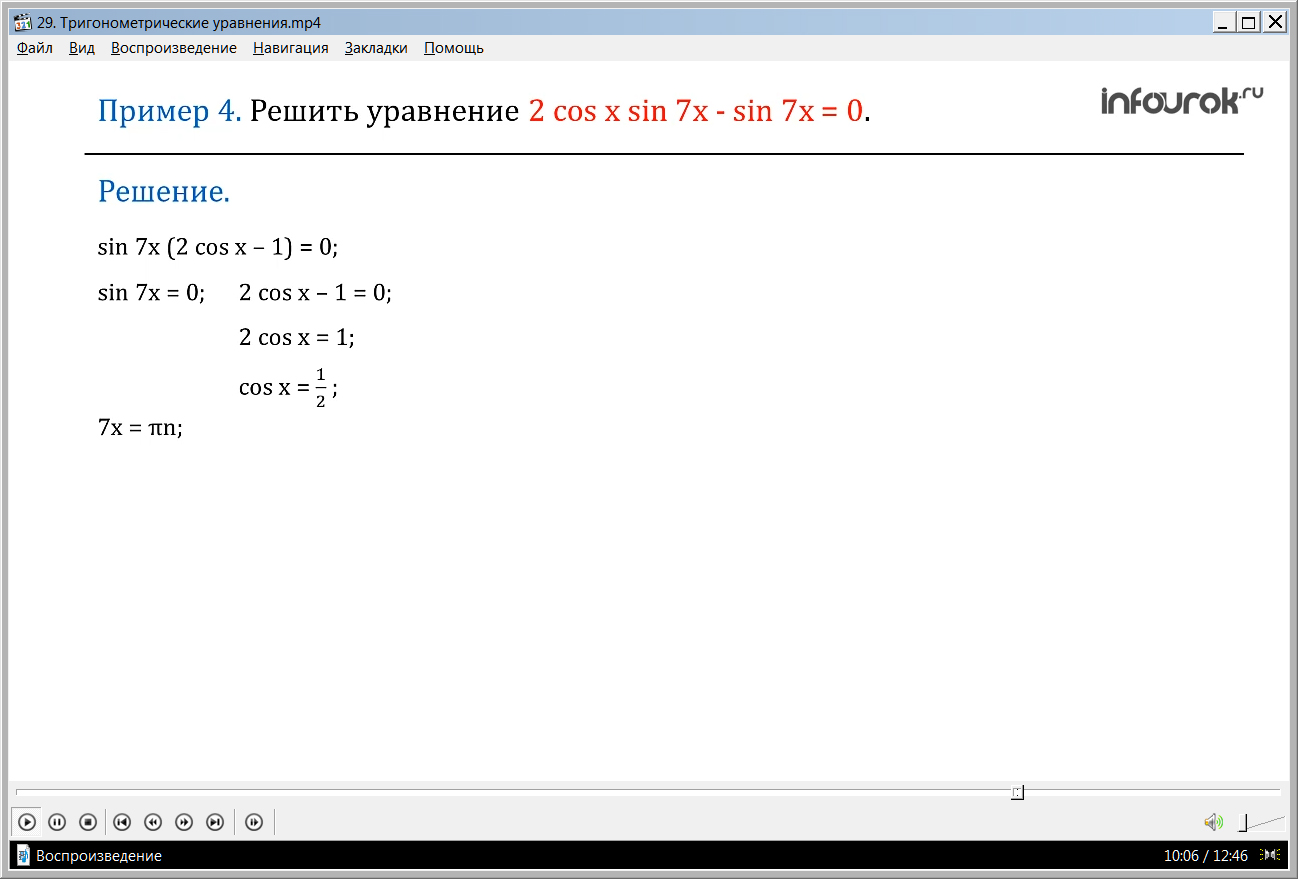
ПРИМЕР 4. Решить уравнение 2 cosхsin7x - sin 7x = 0.( два косинус икс на синус семи икс минус синус семи икс равно нулю)
Решение. Используем метод разложения на множители.
Вынесем за скобку sin 7x, получим sin 7x(2 cosх – 1) =0. Перейдем к совокупности уравнений:
Так как мы помним, что при а=0 х = πn,
то из первого уравнения находим, что 7х = πn, значит, х = .
Так как Решения уравнения cosx =a, при | а | 1, имеют вид:
х = arccosa + 2πn, а а=,
то из второго уравнения находим: х = arccos + 2πn,
А так как из определения арккосинуса числа а следует, что arccos это такое число, косинус которого равен
cos= , значит arccos = Подставив данное значение в найденное выражение х = arccos + 2πn, находим, что х = + 2πn.
ЗАМЕЧАНИЕ. При переходе от уравнения вида f1(x) ∙ f2(x) = 0 нужно быть очень внимательным.
Рассмотрим, например, уравнение ctgх(cosх – 1) =0.
1. Перейдем к совокупности уравнений:
Из уравнения ctg х= 0 находим по таблице значений котангенса: arcctg 0=, тогда х = + πn,
а из уравнения cos х =1 находим х .
Вспоминаем частные случаи:
Значит х= 2πn.
Но включить в ответ второе решение нельзя, потому что при значениях х = 2πn множитель ctgх не имеет смысла, т.е. значения х = 2πn не принадлежат области определения уравнения (или по-другому области допустимых значений – ОДЗ). Значит х = 2πn - это посторонние корни.
Ответ х = + πn, .
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 13937 |
| Номер материала | 857 |