
Урок "Угол между векторами"

Краткое описание документа:
Видеоурок «Угол между векторами» представляет наглядный материал для ведения урока по теме. В ходе видеоурока рассматривается понятие угла между векторами, возможное взаимное расположение векторов в зависимости от того, какой угол образуется между ними. Видеоурок может помочь учителю сформировать представление об изучаемом понятии, сопровождая его объяснение наглядным материалом. Также пособие может использоваться как самостоятельная часть урока, освобождая учителя для того, чтобы уделить больше внимания индивидуальной работе с учениками.
Видеоматериал является наиболее эффективным наглядным пособием из всех современных способов наглядности. В нем не только четко и понятно изображены иллюстрации и построения, но также имеется звуковое сопровождение, в котором предусмотрены важные комментарии учителя, облегчающие понимание предмета изучения. Видео составляется с использованием анимационных эффектов, выделения математических объектов, формулировок и понятий цветом. Используя видеоурок, учитель может значительно повысить эффективность урока математики.
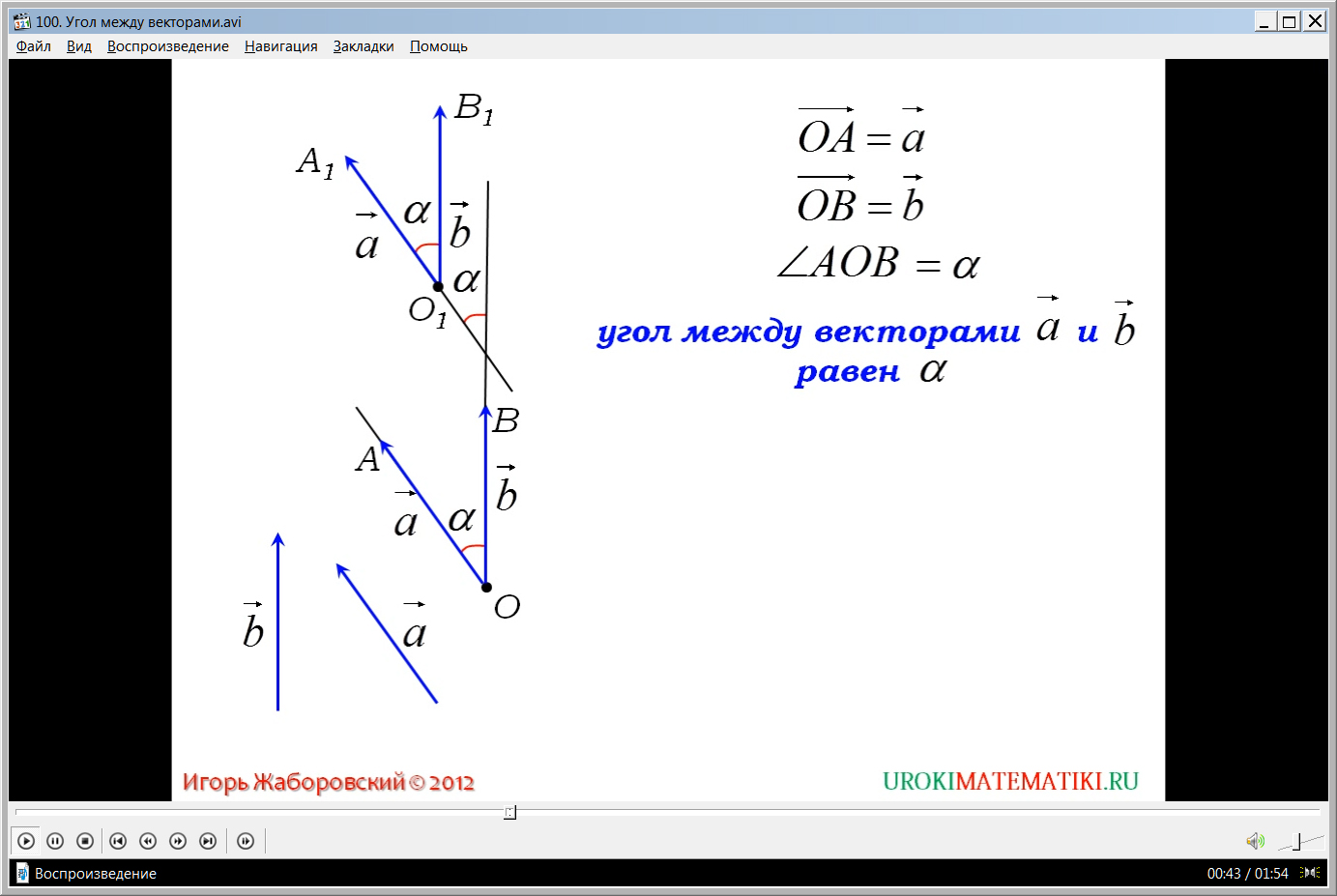
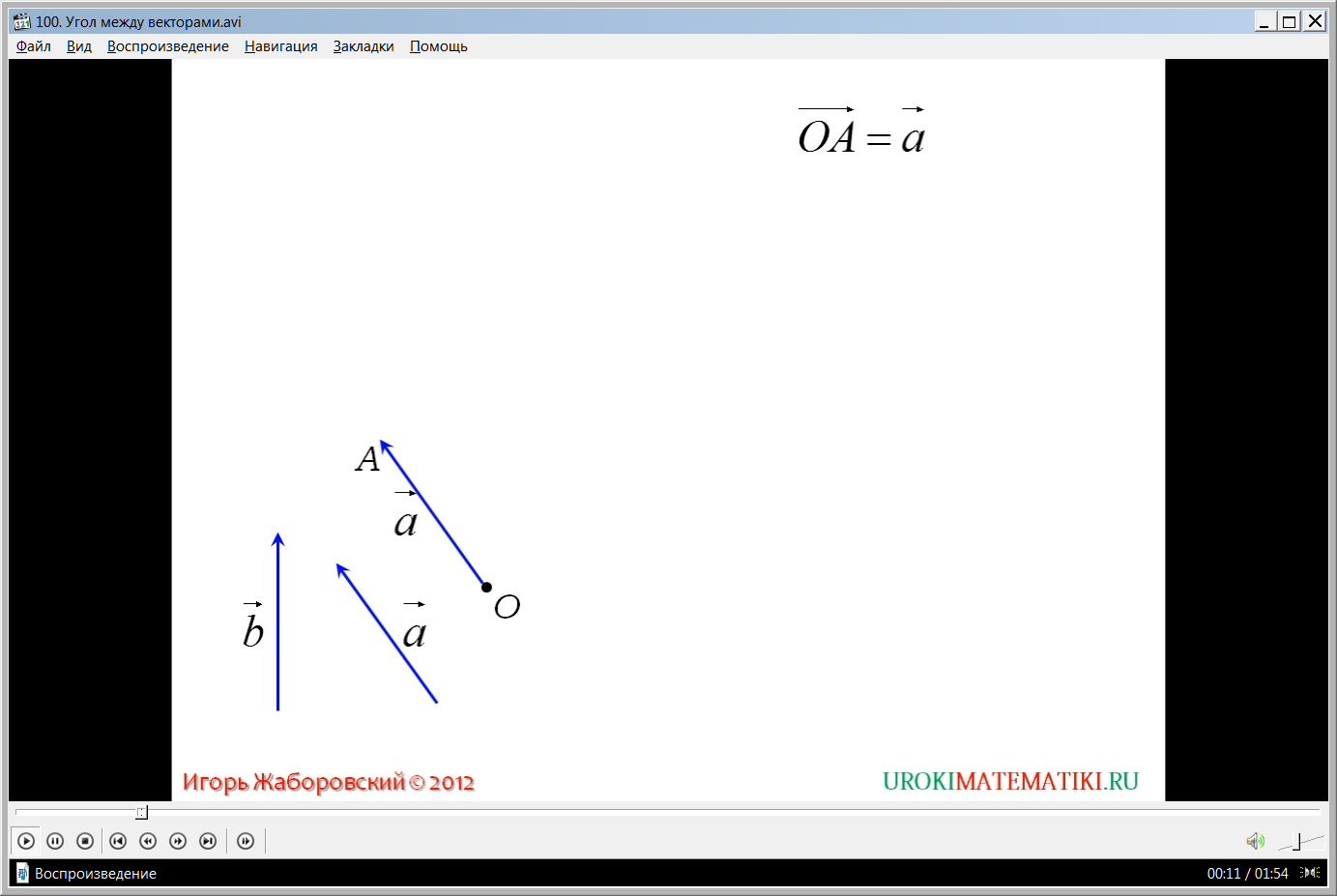
Демонстрация начинается с представления темы видеоурока. На экране продемонстрированы два произвольных вектора aˉ и bˉ. Для введения понятия угла между данными векторами необходимо их переместить таким образом, чтобы они выходили из одной вершины. Для этого отмечается некоторая точка О, их которой строится вектор ОАˉ, параллельный вектору аˉ. Затем из этой же точки строится вектор ОВˉ, параллельный и равный вектору bˉ. Рядом с рисунком отмечается, что ОАˉ= аˉ, а ОВˉ= bˉ. Так как данные в условии вектора не сонаправлены, то лучи, построенные из этих векторов, образуют угол ∠АОВ. Вводится обозначение угла между векторами на плоскости, соответствующее обозначению обычного линейного угла. Угол называют α. Представляется математически корректное выражение, которое необходимо применять при рассмотрении темы – угол между векторами aˉ и bˉ равен α. Также отмечается независимость выбранного начала построения - точки О. На рисунке продемонстрировано, что при выборе другой точки О1 таким же образом будет построен угол между векторами aˉ и bˉ с концами в других точках А1 и В1. При этом угол между векторами равен построенному ранее углу.
Далее рассматривается частный случай – когда векторы aˉ и bˉ сонаправлены. На рисунке изображены сонаправленные вектора aˉ и bˉ, а также вектора aˉ и bˉ, с нулевым вектором bˉ. Отмечается, что для таких векторов угол будет считаться 0°. Также введено обозначение в математической записи угла между векторами aˉ^bˉ.
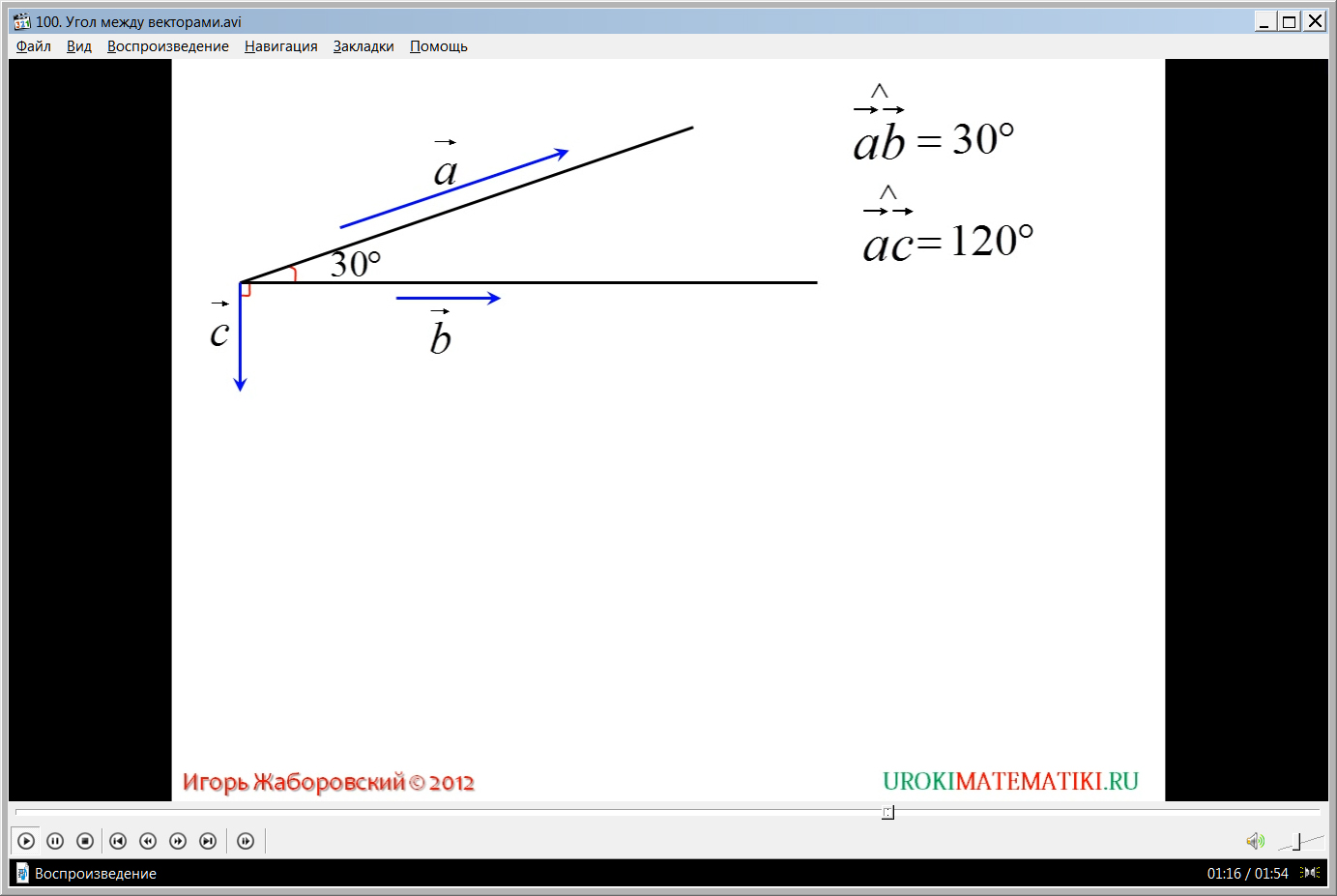
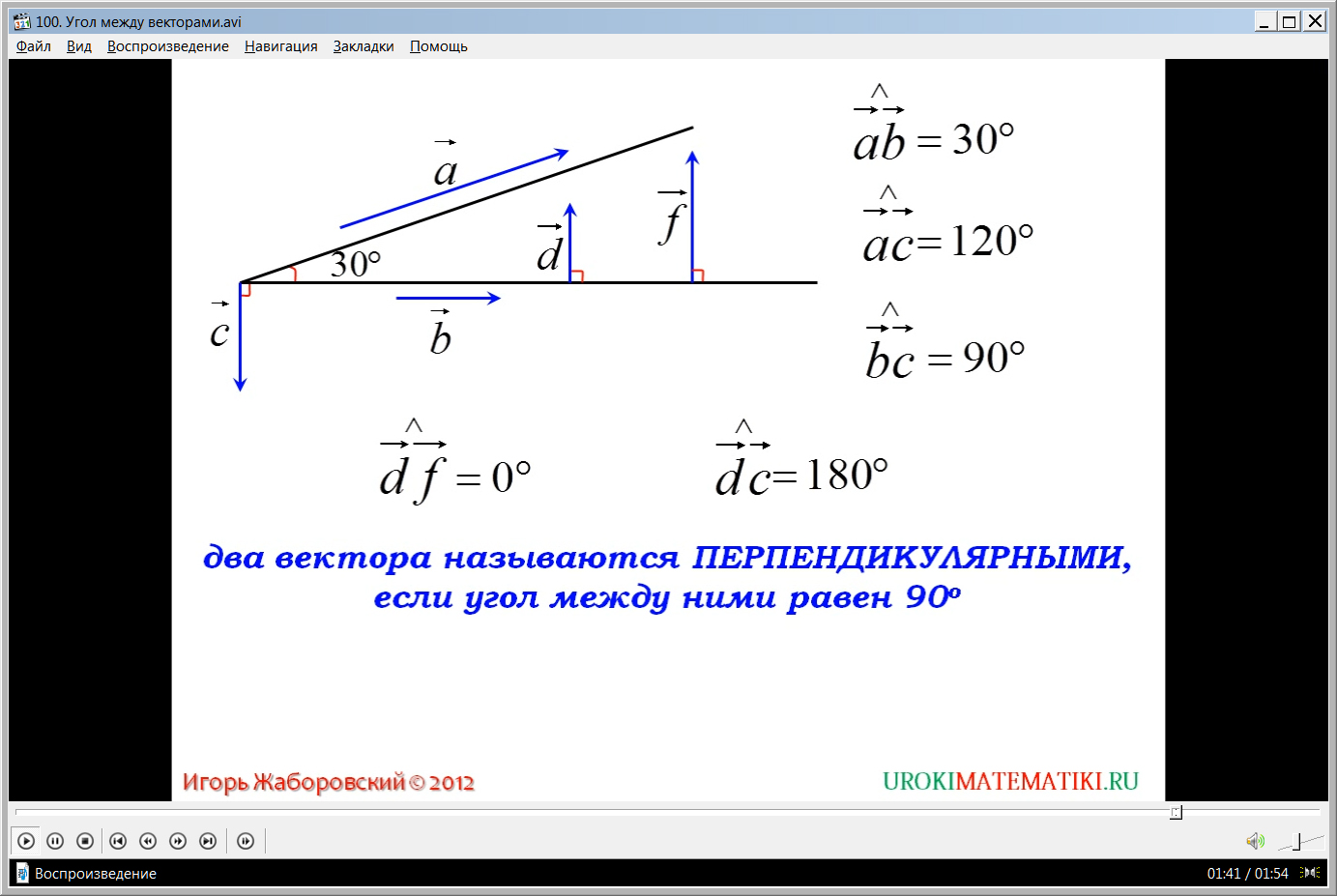
На рисунке строится угол 30°, отмечая, что стороны угла представлены векторами aˉ и bˉ. Отмечается, что запись угла между векторами выглядит так: aˉ^bˉ=30°. Из вершины угла строится еще один угол перпендикулярно вектору bˉ. Отмечается, что угол bˉ^сˉ=90°. Также демонстрируется построение сонаправленных векторов dˉ и fˉ. При этом угол между ними отмечается как dˉ^fˉ=0°. Построенный вектор dˉ составляет с вектором сˉ развернутый угол, поэтому dˉ^сˉ=180°.
Вводится понятие перпендикулярности векторов, угол между которыми составляет 90°. Определение выведено на экран и выделено цветом. Для демонстрации перпендикулярных векторов на рисунке указаны образованные в результате построения пары перпендикулярных векторов bˉ и сˉ, bˉ и dˉ, bˉ и fˉ.
Видеоурок «Угол между векторами» рекомендуется применять на традиционном уроке математики как наглядное пособие. Также данный материал может использоваться учителем, проводящим дистанционное обучение. В качестве дополнительного занятия рассмотрение темы с помощью видеоурока может быть рекомендовано отстающему ученику или изучающему предмет самостоятельно.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 4766 |
| Номер материала | 760 |