
Урок "Уравнение линии на плоскости"

Краткое описание документа:
Видеоурок «Уравнение линии на плоскости» связывает материал, изученный в курсе алгебры об уравнениях и их графиках с геометрическим понятием уравнения линии на плоскости. В ходе видеоурока рассматривается, как составляется уравнение линии на плоскости, какие задачи могут возникнуть в ходе исследования уравнения линии на плоскости. Данный видеоурок может применяться на уроке геометрии вместо объяснения учителем нового материала по данной теме. Задача видеоурока – наглядно представить материал, помочь учителю более эффективно использовать время урока, повысить эффективность обучения.
При помощи данного видеоурока ученики могут лучше усвоить учебный материал. Четкое и понятное построение, которое можно рассмотреть с любой точки в классе, помогает понять особенности связи теоретического материала с практической реализацией. Основные инструменты, воздействующие на процессы запоминания учеников в ходе видеоурока – анимированное построение, выделение цветом, структурированная подача материала, голосовое сопровождение. Такой набор инструментов помогает полностью заменить учителя в процессе обучения на этапе подачи нового материала.
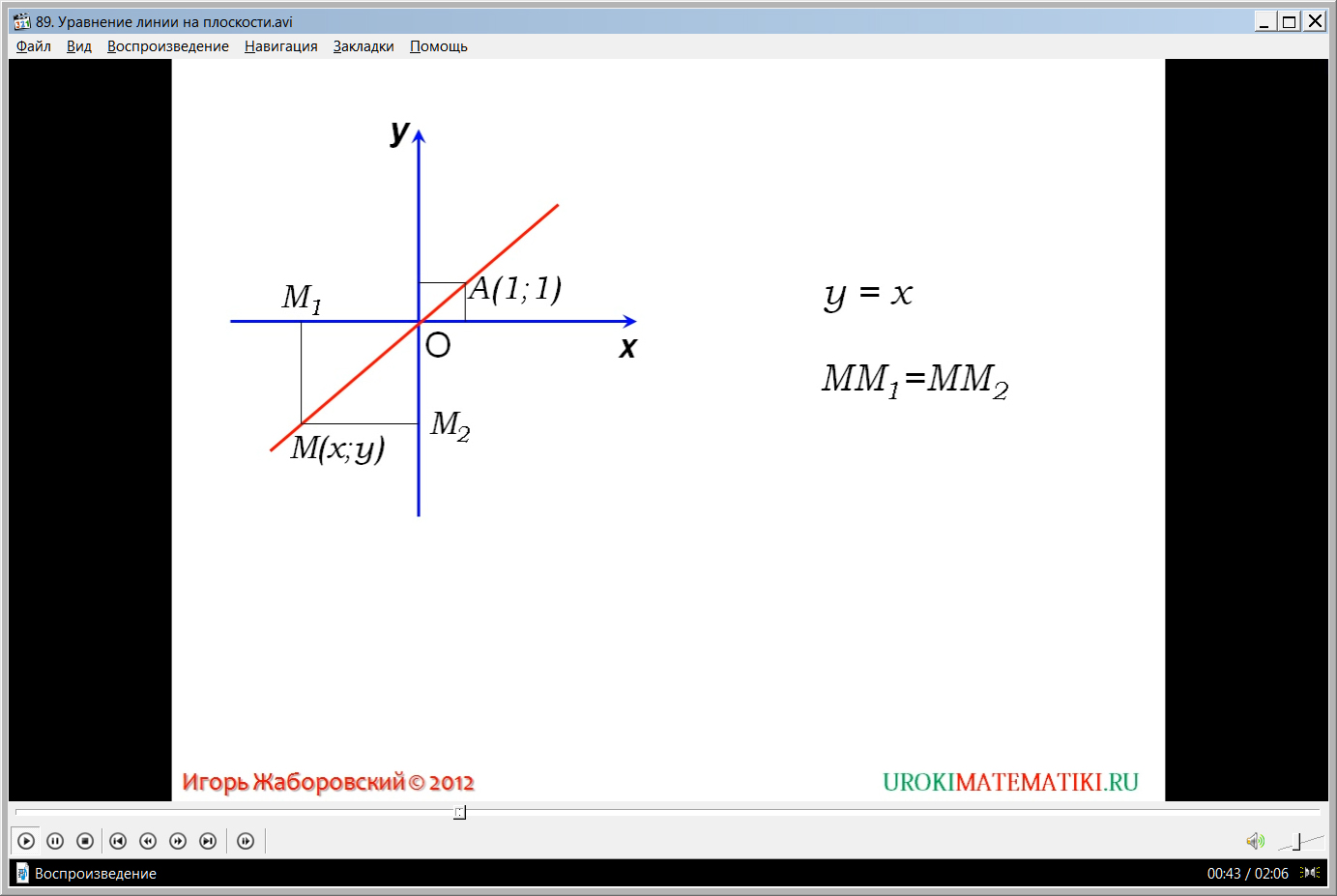
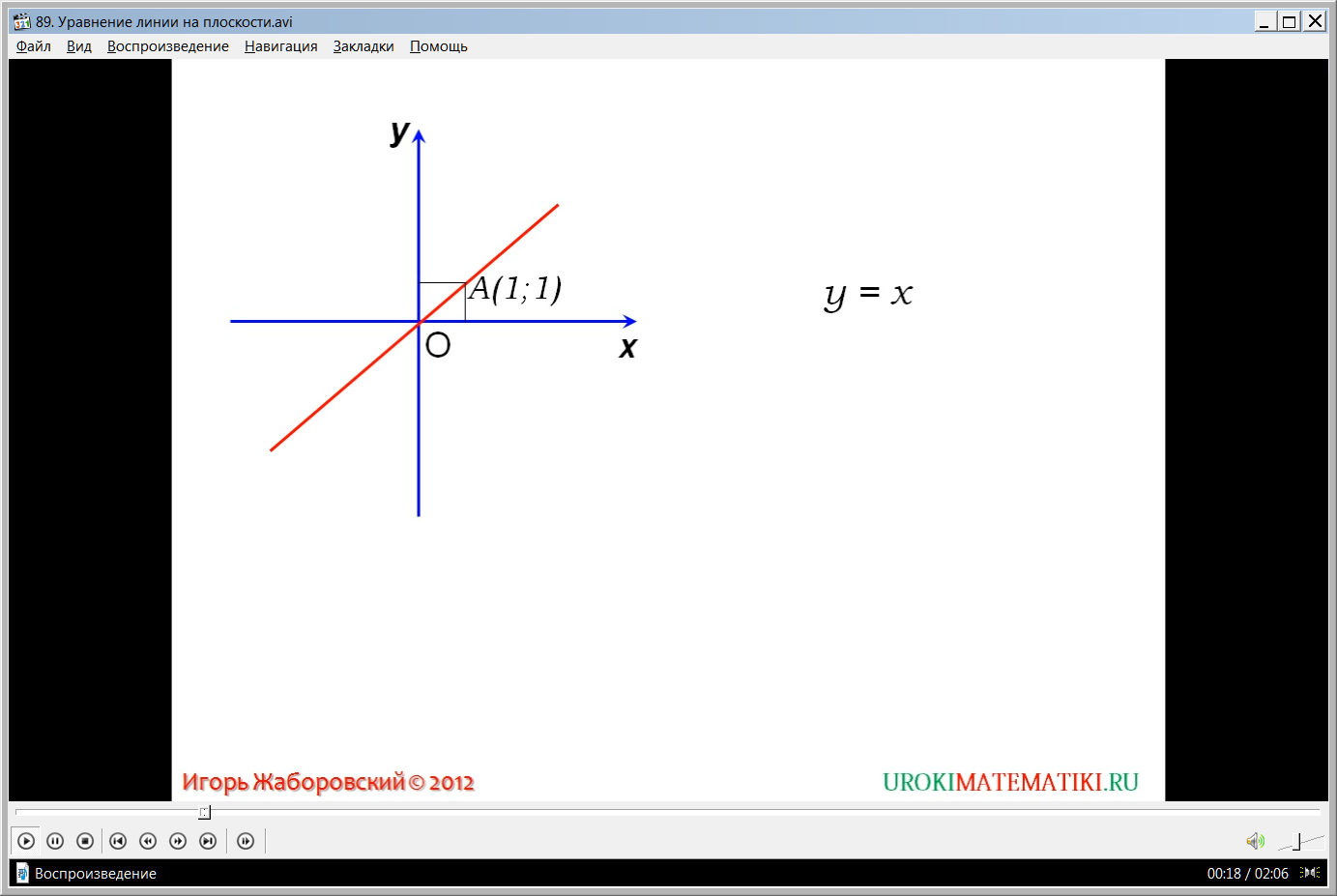
В начале видеоурока ученикам представлена его тема. Далее ученикам напоминается материал, изученный в курсе алгебры. На уроках алгебры они исследовали функции и их графики, связывая уравнение функции с его представлением в прямоугольной системе координат. Примером такой функции может послужить у=х. На экране демонстрируется данная функция, строится прямоугольная система координат и график данной функции – прямая, проходящая через начало координат и через точку с координатами (1;1). Отмечается, что любая точка, лежащая на данной прямой, будет удовлетворять заданному уравнению у=х. На линии, соответствующей прямой у=х, отмечается точка М(х;у), которая демонстрирует соответствие ее координат данному уравнению. От точки опускаются перпендикуляры на оси координат, получая точки пересечения перпендикуляров с осями – М1 и М2. Замечено, что данное уравнение свидетельствует о том, что ММ1=ММ2. При этом, точки, лежащие вне прямой, не будут удовлетворять данному уравнению. В данном смысле можно говорить о том, что прямая у=х является уравнением прямой ОА.
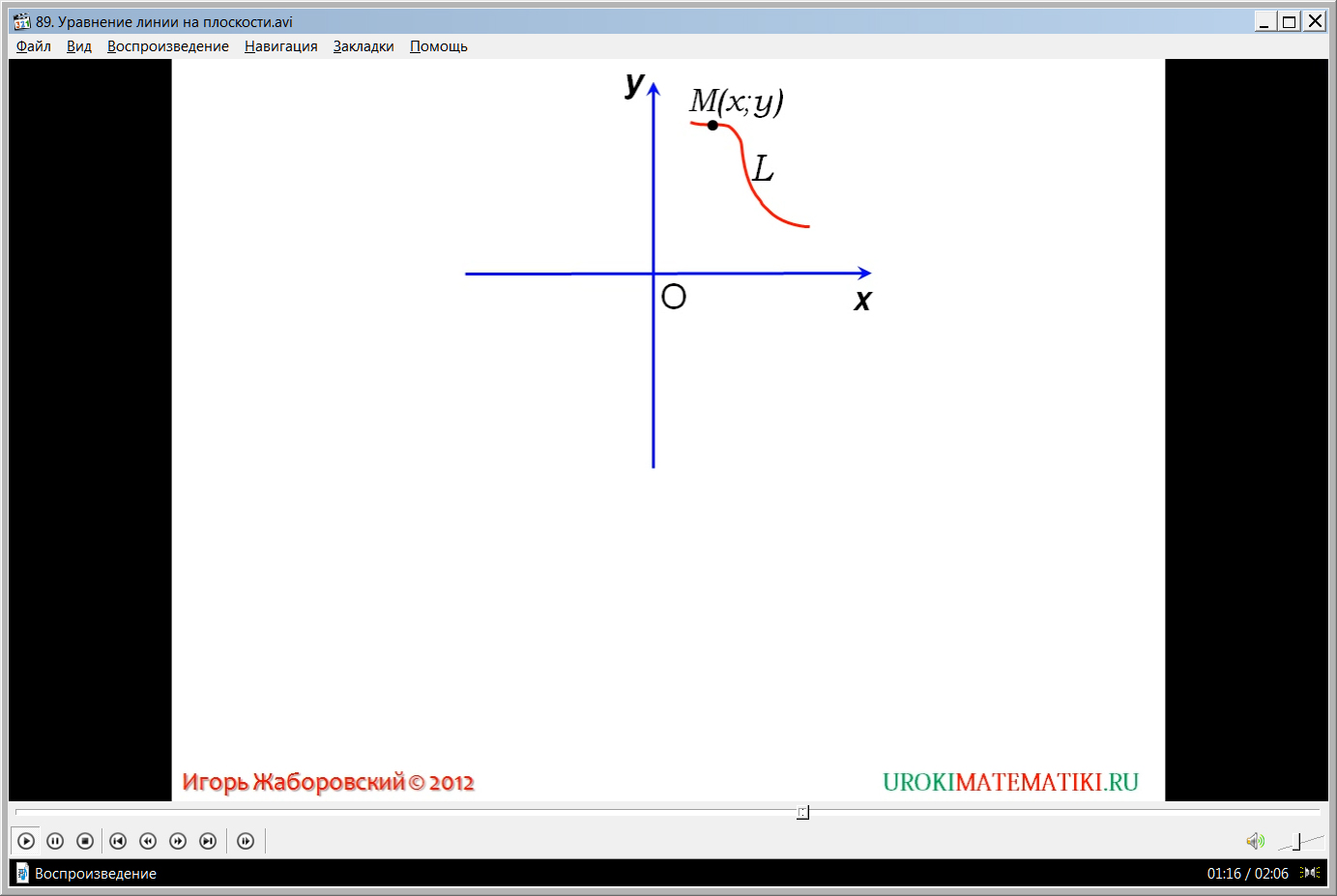
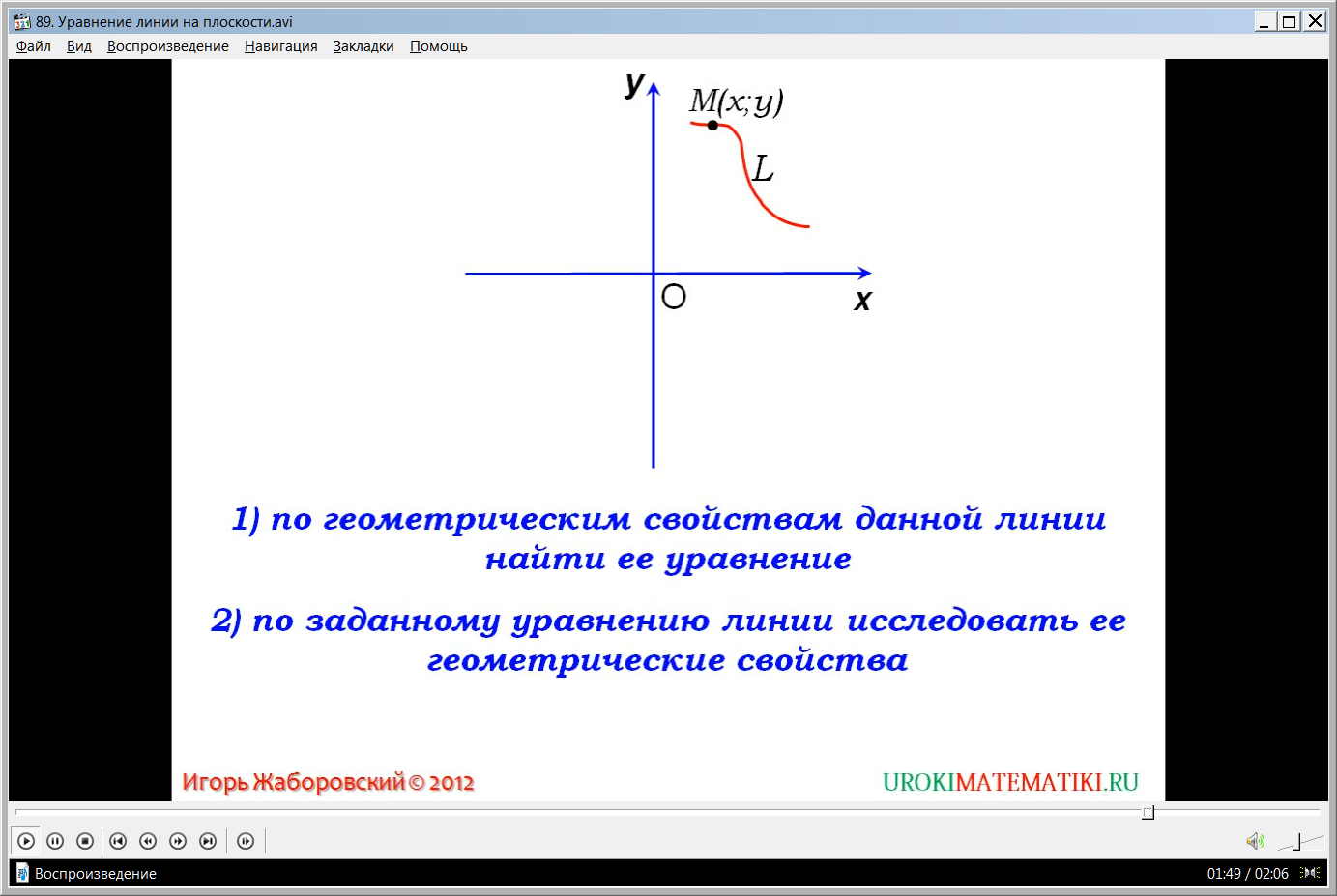
Далее рассматривается уравнение произвольной линии. На экране строится прямоугольная система координат ХОУ, а на ней произвольная линия L. Отмечается, что уравнением данной линии будет уравнение, которое верно для любой точки М(х;у), принадлежащей данной линии. При этом координаты всех остальных точек, лежащих вне линии, не удовлетворяют данному уравнению. Практические задачи, которые возникают в ходе исследования связей линии и ее уравнения, бывают двух типов – определить уравнение линии по известным ее геометрическим свойствам, и второй тип задачи – по имеющемуся уравнению исследовать геометрические свойства данной линии. Отмечая последовательность курса изучения данной темы, отмечается, что на следующем уроке отводится время для рассмотрения решения задач первого типа, применительно к произвольной окружности. Задачи второго типа уже рассматривались учениками при изучении курса алгебры, когда исследовались различные виды функций, их свойства и графики.
Видеоурок «Уравнение линии на плоскости» может послужить наглядным пособием на уроке геометрии в школе. Также данный урок будет полезен ученикам для более глубокого понимания материала при самостоятельном его изучении. В ходе дистанционного обучения видеоурок помогает обеспечить наглядность в изучении новой темы.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 4804 |
| Номер материала | 771 |