
Урок "Уравнение окружности"

Краткое описание документа:
Видеоурок «Уравнение окружности» дает представление об уравнении окружности, раскрывает метод выведения уравнения окружности с известным радиусом и координатами центра. В ходе урока рассматриваются примеры, которые помогают усвоить материал и научить применять его на практике в решении задач. Задача данного пособия – облегчить восприятие материала, способствовать его запоминанию, позволить учителю более рационально распределить время урока, повысить эффективность обучения. Освобожденное время учитель может использовать на повышение качества индивидуальной работы с учениками.
В ходе видеоурока используются следующие эффекты – анимация, структурирование материала по кадрам, выделение цветом важных понятий и деталей построения и теоретической части. Видеоуроки помогают сконцентрировать внимание учеников на изучении темы. Структурированная, четкая подача материала улучшает его восприятие. Последовательное объяснение с построением, голосовым сопровождением дает возможность улучшить усвоение материала учениками с различными способностями и особенностями внимания.
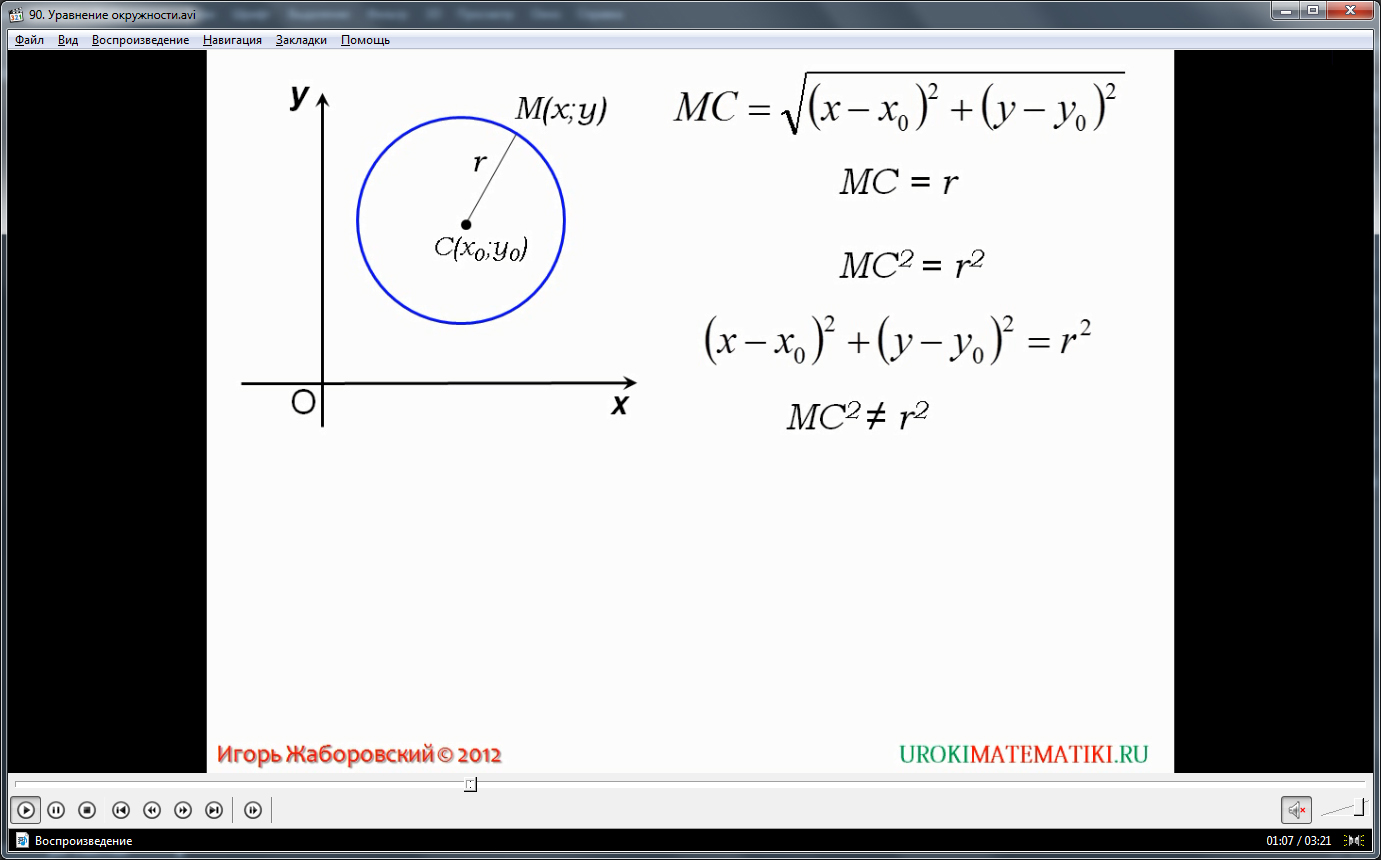
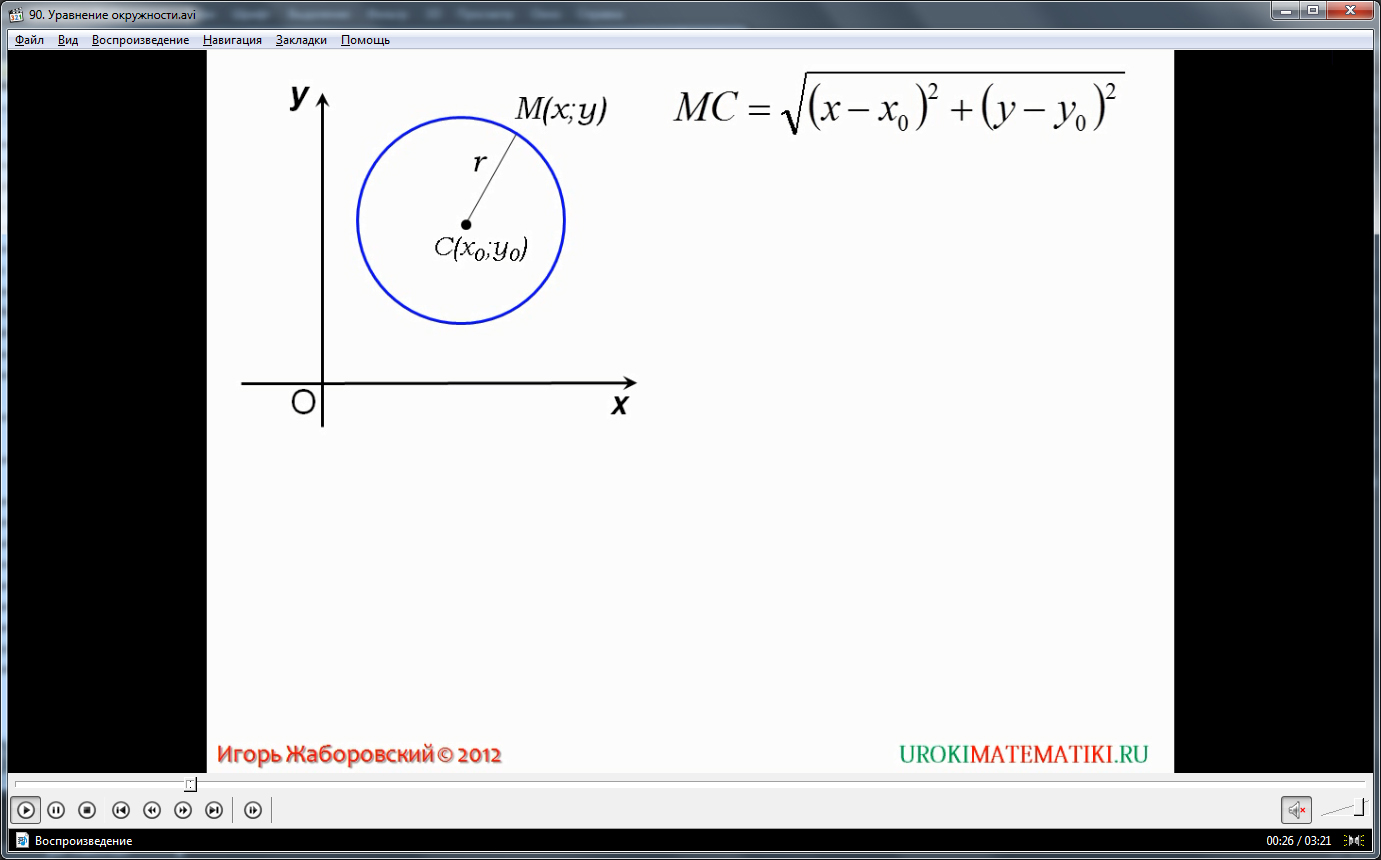
Видеоурок начинается с представления темы урока. На экране строится прямоугольная система координат, на которой нарисована окружность с центром в точке С(х0;у0). Также в данной окружности отмечен радиус r. По известным свойствам окружности расстояние между ее центром и любой точкой М(х;у), принадлежащей окружности, будет вычисляться по формуле, уже изученной на прошлых уроках. Соответственно, расстояние между точкой М(х;у) и С(х0;у0) будет представлено формулой МС=√(х-х0)2+(у-у0)2. Так как данное расстояние в окружности представлено радиусом, верно равенство МС=r. Возведя в квадрат обе части равенства, получим МС2=r2. Подставив вместо МС выражение, отражающее расстояние между точками в системе координат, получаем (х-х0)2+(у-у0)2= r2. Также отмечается, что данное уравнение не будет верно для любой другой точки, которая лежит вне данной окружности. Из рассуждения делается вывод, что уравнение окружности, имеющей радиус r и центр в точке С(х0;у0) в прямоугольной системе координат выражается следующим равенством (х-х0)2+(у-у0)2= r2.

Отдельно выведено уравнение окружности, центр которой располагается в начале координат. В этом случае координаты центра окружности равны нулю. Уравнение окружности преобразуется в вид х2+у2= r2.
Для усвоения рассмотренного материала приводится пример нахождения уравнения окружности. В примере необходимо описать уравнение окружности, которая проходит через начало координат, а центр имеет в точке (-3;4). Зная, что центр окружности располагается в точке (-3;4), записываем уравнение, пользуясь изученной формулой (х+3)2+(у-4)2= r2. Чтобы определить радиус окружности r, необходимо воспользоваться заданным условием, что окружность проходит через начало координат. Чтобы определить радиус, подставляем значение координат данной точки в уравнение (0+3)2+(0-4)2= r2. После вычислений получаем r2=25. Вычисленный радиус окружности r=5. В результате анализа получаем готовое уравнение окружности (х+3)2+(у-4)2= 25. Данное уравнение после раскрытия скобок принимает вид х2+у2+6х-8у=0. Данное уравнение также является уравнением окружности.

Видеоурок «Уравнение окружности» может применяться на уроке геометрии как наглядное пособие при изучении данной темы. Видеоматериал может стать дополнительным пособием, помогающим ученику самостоятельно освоить данную тему или углубить ее понимание. Наглядность пособия поможет учителю, осуществляющему дистанционное обучение.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 6999 |
| Номер материала | 770 |