
Урок "Уравнение прямой"

Краткое описание документа:
Видеоурок «Уравнение прямой» содержит наглядный материал для усвоения данной темы. В видеоуроке выводится уравнение прямой, рассматриваются его особенности. Задача данного пособия – способствовать улучшению усвоения нового учебного материала, помочь учителю наглядно представить тему, помочь ученикам запомнить важные теоретические положения, научиться решать геометрические задачи по данной теме. Данный материал может быть использован на этапе объяснения нового материала в качестве самостоятельного блока подачи материала. Также данный материал может сопровождать объяснение учителя. Использование видеоурока повышает эффективность урока, освобождая учителя для проведения более качественной индивидуальной работы.
В данном видеоуроке используются инструменты, которые помогают удержать внимание ученика на изучаемом предмете, улучшить восприятие материала, сформировать глубокое понимание предмета. Последовательная структурированная подача материала способствует логически верным выводам. Использование анимации приближает построения и выведение формул к обычному представлению учебного материала. При этом на экране все построения четкие, хорошо видны всем ученикам. Выделение цветом важных понятий и деталей позваоляют акцентировать на них внимание и улучшить запоминание выводов и формулировок.
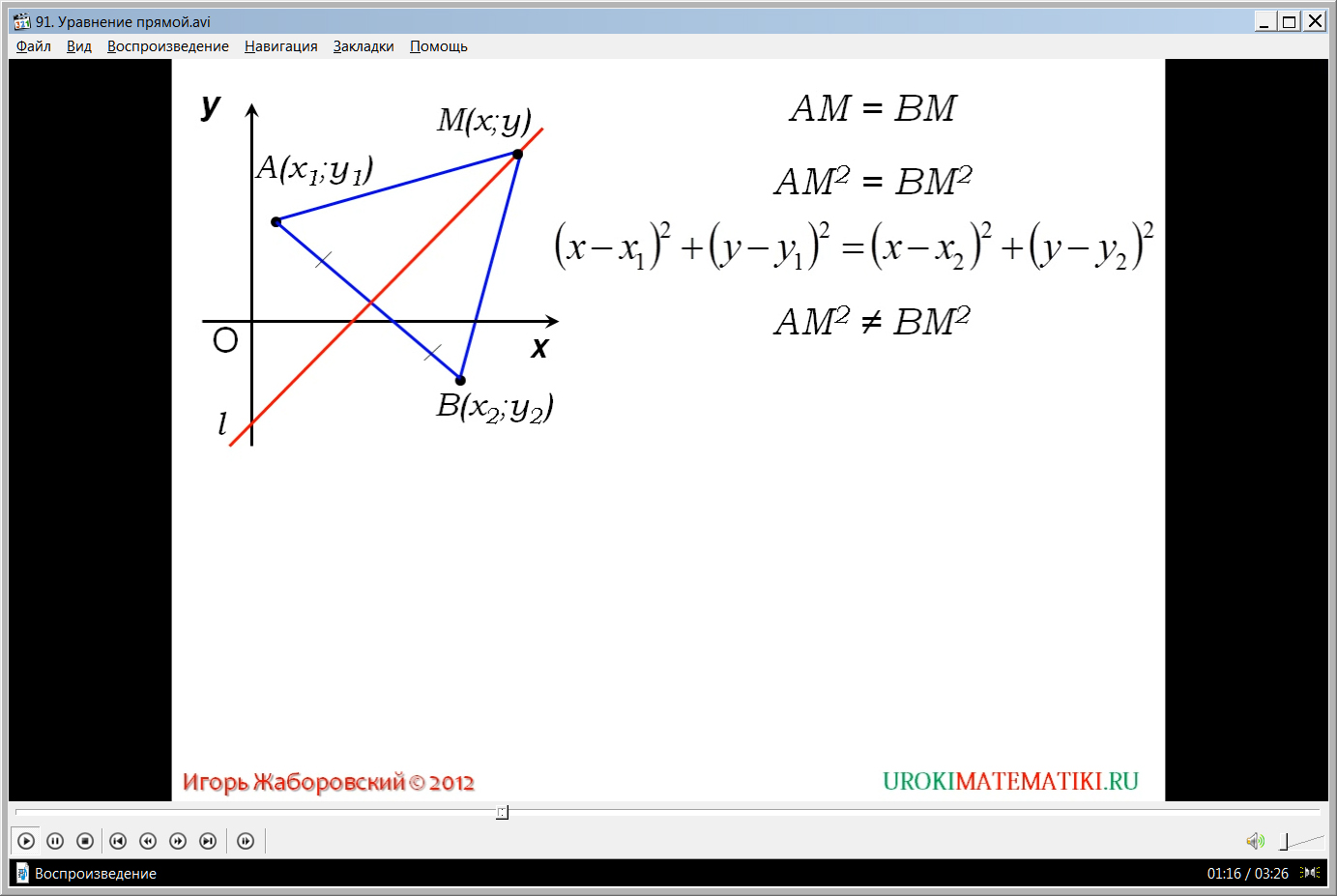
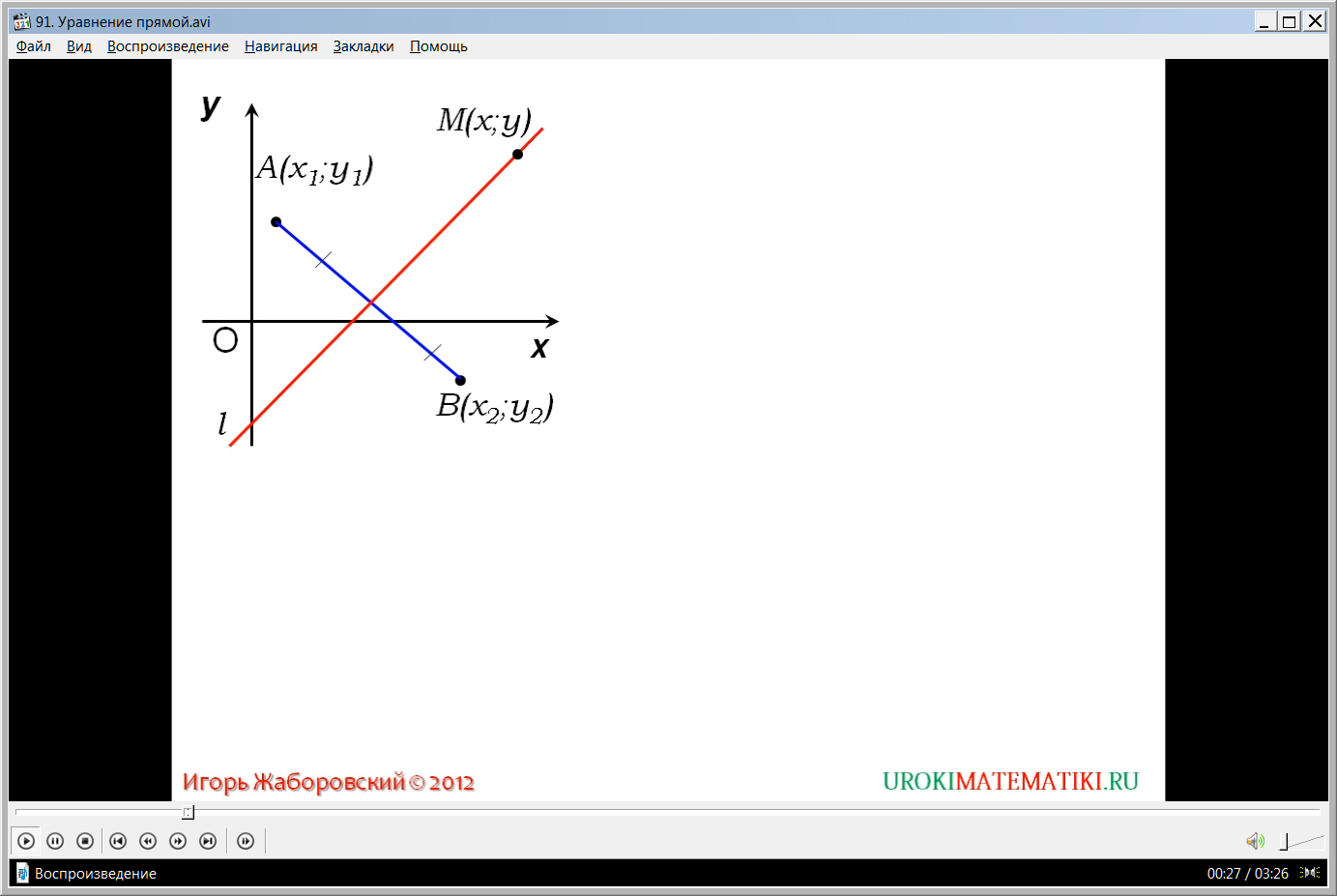
Видео начинается с представления темы урока и построения прямоугольной системы координат ХОУ. На данной координатной плоскости отмечаются две точки А(х1;у1) и В(х2;у2). Точки строятся таким образом, чтобы прямая l, которая располагается на плоскости, была серединным перпендикуляром к данному отрезку АВ. Выберем на прямой l некоторую точку М(х;у). Очевидно, так как прямая l является серединным перпендикуляром отрезка АВ, длины отрезков АМ и ВМ будут равны АМ=ВМ. Возведя в квадрат обе стороны равенства, получаем АМ2=ВМ2. Используя имеющуюся формулу, выражающую расстояние между точками через координаты точек, получаем равенство (х-х1)2+(у-у1)2=(х-х2)2+(у-у2)2. Любая точка, лежащая вне прямой l, не будет удовлетворять равенству, то есть АМ2≠ВМ2. И координаты точки вне прямой также не будут удовлетворять описанному равенству. Значит, данное уравнение является уравнением прямой l в данной системе координат. После приведения подобных слагаемых в данном равенстве уравнение примет вид ах+by+c=0. В данном уравнении а=2(х1-х2), b=2(у1-у2), коэффициент с=х22+у22-х12-у12. Уравнение ах+by+c=0 является уравнением прямой. Оно выведено на экран и взято в рамку для запоминания. Отмечается, что так как точки А и В не совпадают, то какая-либо разность их координат х1-х2 или у1-у2 не будет равна нулю. Из сделанного анализа формулируется вывод, что уравнение прямой в прямоугольной системе координат – уравнение первой степени.

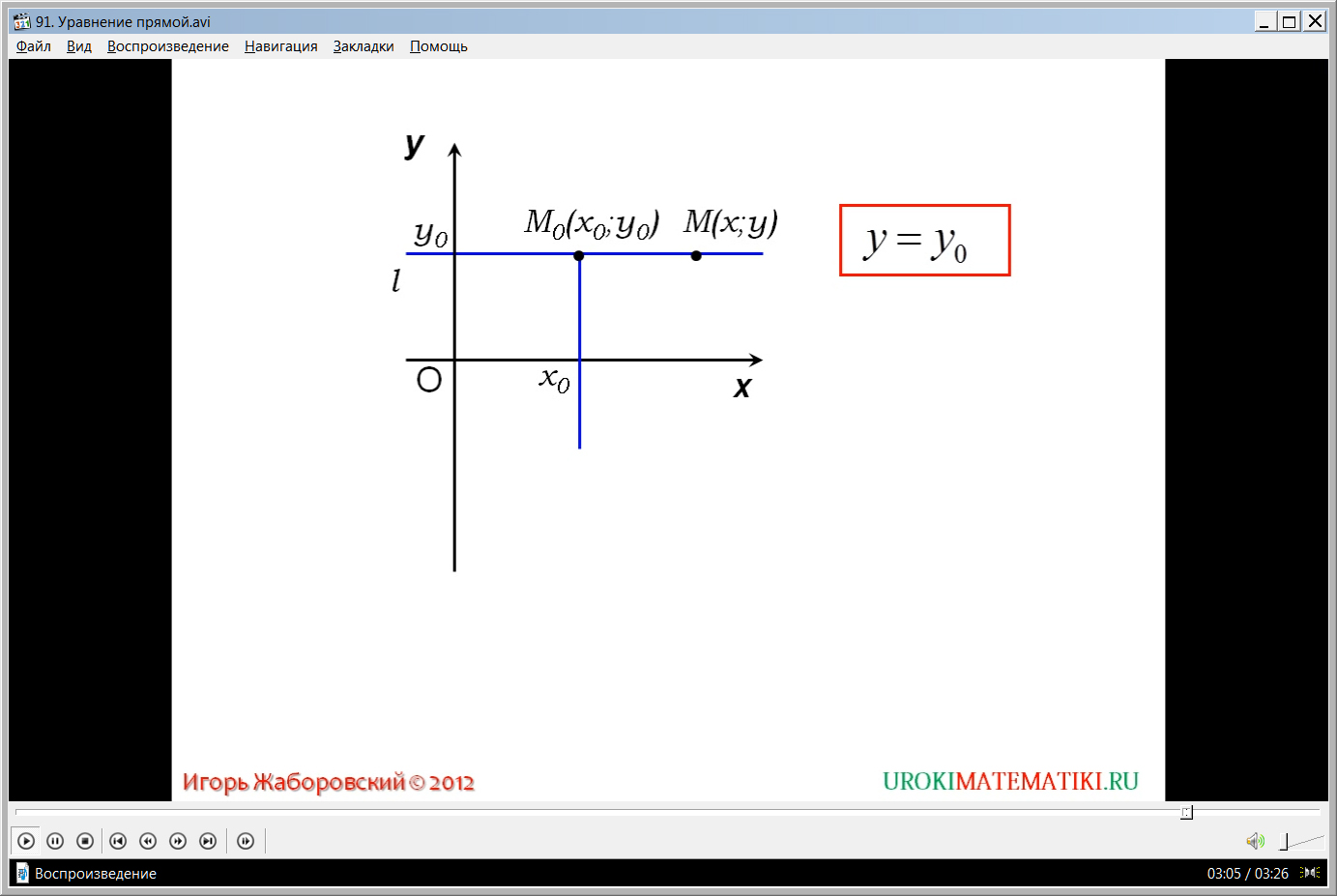
Далее предлагается рассмотреть выведение уравнения прямой, которая проходит через точку М(х0;у0) и расположена параллельно оси Ох. Отмечается, что любая точка М(х;у), принадлежащая данной прямой, имеет ординату у0. Это значит, что каждая точка прямой удовлетворяет уравнению у=у0. При этом любая точка координатной плоскости, которая не принадлежит данной прямой, не соответствует указанному уравнению. Значит, выведенное уравнение у=у0 является уравнением данной прямой.
Аналогично предыдущему примеру рассматривается выведение уравнения прямой, проходящей через точку М(х0;у0) расположенной параллельно оси ординат. То, что прямая параллельна оси ординат означает, что любая точка, которая принадлежит данной прямой, имеет абсциссу х0. Поэтому уравнение данной прямой будет иметь вид х=х0. Проанализировав подобным образом прямую, совпадающую с осью абсцисс, получаем ее уравнение у=0. Уравнение прямой, совпадающей с осью ординат, будет равно х=0.
Видеоурок «Уравнение прямой» может быть использован в качестве пособия в школе на уроках геометрии по данной теме. Также данный видеоматериал поможет ученикам самостоятельно разобраться в особенностях выведения уравнения прямой, научиться выводить такое уравнение самостоятельно. Наглядность и подробное описание учебного материала поможет учителю донести предмет изучения до ученика в ходе дистанционного обучения.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 6256 |
| Номер материала | 769 |