
Урок "Вычисление производных"

Краткое описание документа:
Видеоурок «Вычисление производных» имеет большое практическое значение, так как в течение этого урока формируется умение решать задачи на нахождение производной различных функций. В течение урока предоставляются сведения о производных основных математических функций, свойствах производных, демонстрируется решение заданий с применением знаний о свойствах производных и производных основных функций.
Видеоурок начинается с представления его темы. Вводится понятие формул дифференцирования – формул, необходимых для отыскания производных определенных функций. В качестве примеров таких формул представлены С′=0, х′=1, (kx+m)′=k, (x2)′=2x, (x3)′=3x2, (1/x)′=-1/x2, (√х)′=1/2√х, (sin x)′=cos x, (cos x)′=-sin x.
Далее демонстрируется применение изученных формул для нахождения значения производных функций. В примере 1 дается 6 функций, предел которых нужно определить:
а) у=-2х+7 в точке х=√5. Подставив значения в формулу, определяем у′=-2. Поэтому и у′(√5)=-2.
б) у=х2 в точке х=-2. После подстановке выражения в соответствующую формулу находим у′=2х. Поэтому у′(-2)=-4.
в) у=1/х в точке х=1/3. Выбрав соответствующую формулу, находим у′=-1/х2. Поэтому у′(1/3)=-9.
г) у=√х в точке х=9. Подставив в формулу, находим у′=1/2√х. Поэтому у′(9)=1/6.
д) у=sin x в точке х=π. Зная формулу, находим у′=cos x. Это означает у′(π)=-1.
е) у=cos x в точке π/4. Производная у′=-sin x, а в данной точке у′(π/4)=-√2/2.
В примере 2 рассматривается нахождение уравнения касательной к графику у=х2 в точке х=-1. Ученикам напоминается, что уравнение касательной представляет собой прямую, определенную уравнением y= kx+m. Значение производной функции в точке – угловой коэффициент касательной. Находим производную в точке у′=( х2)′=2х, у′(-1)=-2. Это коэффициент k. Для нахождения m подставляем значение функции в уравнение прямой. Зная, что в точке х=-1, у= х2=1, получаем уравнение 1=(-2)·(-1)+m. Отсюда m=-1. Получаем уравнение касательной у=-2х-1.
Далее демонстрируется выведение формул для нахождения производных некоторых функций. Сначала находится производная у=√х. Согласно алгоритму нахождения производной, находим для фиксированного значения х значение функции f(x)=√x. После изменения аргумента х+Δх функция получает значение f(х+Δх)=√( х+Δх). Приращение функции при изменении аргумента равно f(х+Δх)- f(x)=√( х+Δх)- √x. Находим отношение Δу/Δх=(√( х+Δх)- √x)/Δх. После преобразования выражения получаем Δу/Δх=1/(√( х+Δх)+√х). При стремлении Δх→0 находим предел отношения lim Δу/Δх=1/2√x. Производная (√x)′= 1/2√x.
Согласно агоритму нахождения производной также опредляется производная y=sin x. В некоторой фиксированной точке х значение функции f(x)= sin x. После изменения аргумента х+Δх получаем значение функции f(х+Δх)= sin ( х+Δх). Находим приращение функции f(х+Δх)- f(x)= sin ( х+Δх)- sin x. После преобразования выражения получаем f(х+Δх)- f(x)=2 sin(Δх/2)cos(x+Δx/2). Находим отношение Δу/Δх=( sin ( х+Δх)- sin x)/Δх=2 sin(Δх/2)cos(x+Δx/2)/ Δх. Приняв t= Δх/2, получаем выражение Δу/Δх=sin t cos(x+t)/ t. Предел отношения при стремлении Δх→0, lim Δу/Δх= lim sin t cos(x+t)/ t= (lim sin t/t)·lim cos(x+t). Зная замечательный предел lim sin t/t=1 и lim cos(x+t)= cos x, а также воспользовавшись свойством предела произведения находим производную (sin x)′= cos x.
Далее демонстрируются правила дифференцирования. А первом правиле определяется нахождение суммы производных y=f(x), y=g(x). Если производные этих функций существуют в данной точке, то производная их суммы определяется по формуле (f(x)+g(x))′= f′(x)+g′(x). Описывается доказательство правила. Принимаем f(x)+g(x)=h(x). Для постоянной х имеем h(x)=f(x)+g(x). После изменения аргумента x+Δx имеется h(x+Δx)= f(х+Δх)+g(х+Δх). Находим приращение функции Δу= h(x+Δx)- h(x). После подстановки значения h(x) и h(x+Δx) и преобразования выражения, получается Δf+Δ g. Находим отношение приращения значения функции к приращению аргумента Δу/Δх=(Δf+Δg)/Δх=Δf/Δх+Δg/Δх. Это означает, что lim Δу/Δх= f′(x)+g′(x) при Δх→0. Утверждение доказано.
Примером применения правила является нахождение производной (x2+sin x)′= (x2)′+( sin x)′=2x+ cos x.
Доказывается второе правило дифференцирования, которое утверждается о возможности вынесения постоянного множителя за знак производной (kf(x))′= kf′(x). Для постоянного х имеем h(x)= kf(x). После изменения аргумента x+Δx получаем значение функции h(x+Δx)= kf (x+Δx). Приращение функции при этом равно Δу= h(x+Δx)- h(x)= kf (x+Δx)- kf(x)= kΔf. Отношение приращения функции к приращению аргумента Δу/Δх=k(Δf/Δх). Находим предел отношения при стремлении Δх→0lim Δу/Δх= lim kΔf/Δх=kf′(x). Примером применения данного правила при решении задач служит решение примеров (5х2)′= 5 (х2)′=5·2х=10х и (-cosx/3)′=-(1/3)(cosx)′= -(1/3)(-sinx)=(1/3) sinx.
Третье правило рассматривает нахождение производной произведения двух функций у=f(x) и у= g(х), дифференцируемых в точке х. Оно определяется формулой (f(x)g(x))′= f′(x) g(x)+ f(x)g′(x). В качестве примера применения данного правила демонстрируется нахождение производной функции ((2х+3) sinx)′=(2х+3)′ sinx+(2x+3)(sinx)′=2 sinx+(2x+3) cosx.
Последнее правило регулирует нахождение производной частного двух функций. Ото утверждает, что для функций у=f(x) и у= g(х), дифференцируемых в точке х верно(f(x)/g(x))′= (f′(x) g(x)- f(x)g′(x))/ g2(x). При этом должно быть g(х)≠0, а также существовать производная (f(x)/g(x))′. Для примера применения данного правила при решении задач приводится вычисление (х2/(5-4х))′. Применив формулу, задача разбивается на более простые. В результате преобразований получаем (х2/(5-4х))′=(10х-4х2)/(5-4х)2.
В примере 3 рассматривается нахождение производной у=3х2-4х+2. Применив правило нахождения производной суммы и формулы для нахождения производных от основных функций, получаем у′=(3х2-4х+2)′=( 3х2)′+(-4х+2)′=6х-4.
В примере 4 описывается нахождение производных функций у=х4 и у=х5. С помощью представления функции х4 произведением х3·х определяется (х4)′=4х3. Аналогично определяется (х5)′=5х4. Нахождение производной степенной функции обобщается формулой (хn)′=nхn-1.
В примере 5 рассматривается нахождение точек , в которых касательная у=х3-3х+2 параллельна Ох. Для решения задачи необходимо найти у′=(х3-3х+2)′=3 х2-3. Решением данного уравнения являются точки х=1 и х=-1. В этих точках f(1)=0 и f(-1)=4. Соответственно, решением задачи будут точки (1;0) и (-1;4).
В следующем примере вычисляются производные функций y=tgx и y=ctgx. Для определения производной (tgx)′ используется формула для нахождения тангенса tgx=sinx/cosx. Применив формулу нахождения производной частного, определяется значение производной (tgx)′=1/cos2x. Очевидно, производная не существует в точках х=π/2+2πn. Для вычисления производной используется формула ctgx=1/sin2x.
Далее сообщается о решении обратной задачи наравне с прямой – по известной производной найти функцию. Примером решения такой задачи служит нахождение функции по производной f′(x)=cosx. Отсюда f(x)=sinx. Производную f′(х)=х3 имеет функция f(х)=х4/4. Проверить правильность решения можно, найдя производную f′(х)=( х4/4)′= х3.
Демонстрируется примеры нахождения производной тригонометрических функций, используя формулы преобразования функции двойного аргумента, значения основных производных. На основании этих данных находятся значения производных (sin 2x)΄=2 cos 2x, (cos (-7x))΄=7 sin (-7x), sin√5x=√5cos√5x, (tgx/4)΄=(1/4)·(1/cos2x/4), ((-x+1)5)΄=-5(2x+1)4.
Представлена теорема о нахождении производной от y=f(kx+m). Утверждается, что такая производная вычисляется по формуле y=(f(kx+m))΄= kf΄(kx+m).
В последнем примере находится производная от f(x)=√(8-1,15x) в точке x=5. Пользуясь формулой нахождения производной (√х)΄ и свойством, доказанным в теореме, находится (√(8-1,15x))΄=-1,15/2√8-1,15х.
Видеоурок «Вычисление производных» рекомендуется применять на традиционном уроке математики для повышения эффективности урока, освобождения времени учителя для улучшения обратной связи с учениками. Также данный наглядный материал может облегчить задачу учителя, читающему предмет дистанционно. Для лучшего усвоения темы видеопособие может быть рекомендовано ученикам для самостоятельного рассмотрения.
ТЕКСТОВАЯ РАСШИФРОВКА:
Формулами дифференцирования обычно называют формулы для отыскания производных конкретных функций, например:
С'=0; (цэ штрих равно нулю)
x'=1; (икс штрих равно одному)
(kx+m)' =k; ( ка икс плюс эм штрих равно ка)
(х2)′=2х;
(х3)'=3х2;
Покажем три дополнительные формулы дифференцирования:
(sinх)' =cos х;
(cosх)' = – sin х.
(формулы на экран)
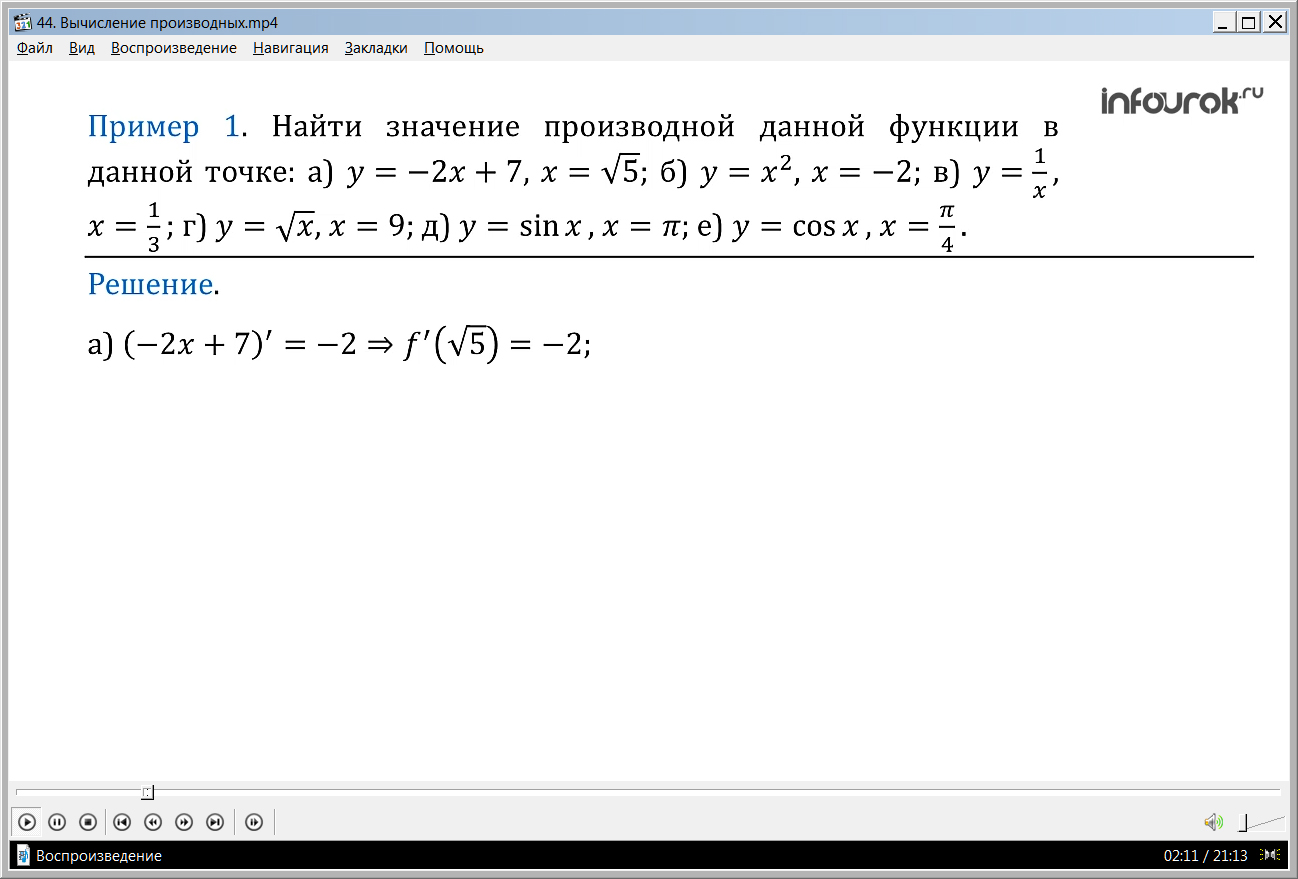
Пример 1. Найти значение производной данной функции в данной точке:
а) у= –2х+7, х= ; б)у = х2, х= –2; в)у =, х=; г)у= , х=9; д) у=sinx, x= 0; e) y=cosx, x=.
Решение, а) Имеем: (–2х + 7)'= –2, (минус два икс плюс семь штрих равно минус два). Значит, производная равна –2 в любой точке х, в частности, в заданной точке х =.
Итак, производная функции у = –2х + 7 в точке х = равна –2; на математическом языке это удобнее записывать так: f'()= –2.(эф штрих от корня из пяти равно минус два)
б) Имеем: (x2)'=2х (производная икс в квадрате равна два икс), значит,
f´(–2) = 2·(–2) = –4.( эф штрих от минус два равно два умножить на минус два равно минус четыре).
в) Имеем: (один, деленное на икс штрих равно минус один, деленное на икс в квадрате), значит, f'= –=–9. (эф штрих от одной третей равно минус девять).
г) Имеем: (корень квадратный из икс штрих равен один, деленное на два корня из икс), значит, f´(9) = = , (эф штрих от девяти равно одной шестой).
д) Имеем: (sinx)'=cosx, значит, f'()=cos = –l.
е) Имеем: (cosx)' =–sinx, значит, f' = –sin= –.
Пример 2. Составить уравнение касательной к графику функции у = х2 в точке х = –1.
Решение. Уравнение касательной, как уравнение всякой прямой, имеет вид y=kx + m. Найдем сначала k– это угловой коэффициент касательной, который, как мы знаем, равен f'(–1).
Имеем: (х2)'=2х, значит, f ′(–l) = 2·(–1)= –2.
Итак, k = – 2, т.е. уравнение касательной будет вида у = –2х + т.
Осталось найти значение коэффициента т. Для этого воспользуемся тем, что касательная проходит через точку с абсциссой х = –1, лежащую на параболе
у = х2 , т.е. через точку (–1; 1).
Имеем:
1=-2•(–1)+m,
m=-1
Итак, уравнение касательной имеет вид у = -2х -1.
Ответ: -2х -1.
Нужен график
(Вывод формул можно вывести на экран рассказав лишь этапы их получения)
Выведем новые формулы дифференцирования.
Найдем производную функции у = .
Воспользуемся алгоритмом отыскания производной.
1) Для фиксированного значения х (при условии, что х > 0) имеем: f(x) = .
2) В точке х+х имеем: f(x+х)=.
3) у = f(x+x) – f(x) = –.
4) = . Здесь полезно применить искусственный прием: домножить и числитель, и знаменатель дроби на выражение +.
В числителе мы получим «разность квадратов»: ()2–()2, т.е.
(х +х)–х или х, а сама дробь примет вид: , т.е. .
Итак, = .
5) = ==
Таким образом, ()'=
В процессе рассуждений мы воспользовались тем, что если
х0, то х +х х и .
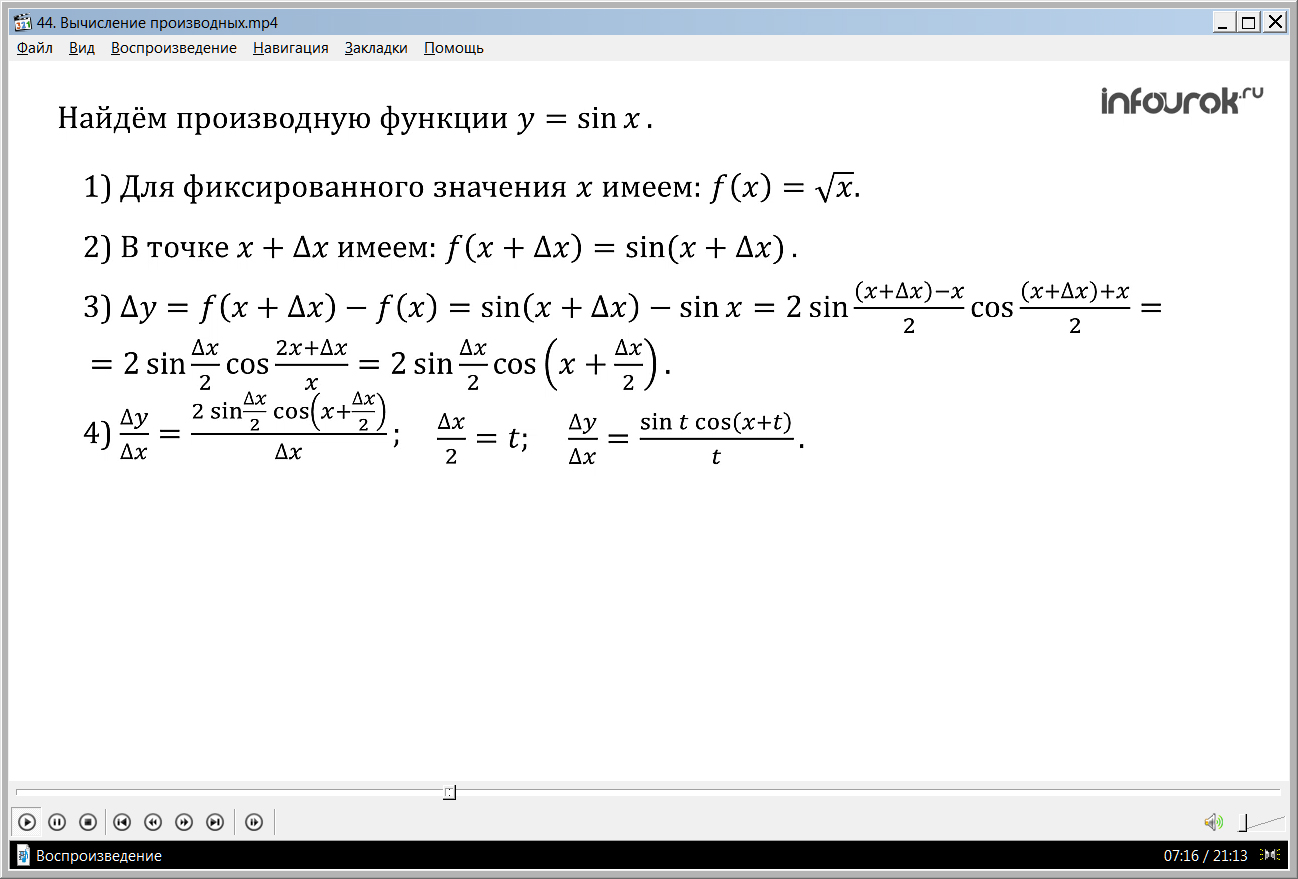
Найдем производную функции у = sinx.
Воспользуемся алгоритмом отыскания производной.
1) Для фиксированного значения х имеем: f(x) = sinx.
2) В точке х+х имеем: f(x+х) = sin(x+x).
3) y = f(x+x)–f(x) = sin(x+x)–sinx. Преобразуем полученное выражение, воспользовавшись формулой «разность синусов»
sin(x+x)–sinx = 2sincos= =2sincos=2sincos
4) =.В правой части полученного равенства – обратите внимание – три раза содержится выражение. Есть смысл обозначить его буквой t. Получим: =
5) = . А далее рассуждаем так: х0, at=, значит, t0 и под знаком предела вместо условия х0 можно записать условие t0.
Таким образом,
Получили произведение пределов. Первый предел – это первый замечательный предел, он равен 1. А второй предел равен cosх. В итоге получаем cosx. Итак, (sin х)' = cos х.
Аналогично выводится формула (cos х)' = –sin х.
2. Правила дифференцирования
Изучим правила нахождения производных суммы, произведения, частного функций.
Правило 1. Если функции y = f(x) и y = g(x) имеют производную в точке х, то и их сумма имеет производную в точке х, причем производная суммы равна сумме производных:
(f(x) + g(x))´= f´(x) + g´(x).
Т.е. производная суммы равна сумме производных.
Докажем данное правило дифференцирования функции у = f(x) + g(x).
Воспользуемся алгоритмом отыскания производной.
1) Положим, ради удобства, f(x) + g(x) = h(x). Для фиксированного значения х имеем: h(x) = f(x) + g(x).
2) В точке х + х имеем: h(x+x) = f(x+x) + g(x+x).
3) у=h(x+x)–h(x)=(f(x+x)+g(x+x))–(f(x)+g(x))=(f(x+x)–f(x))+(g(x+x)–g(x))= f +g.
Итак, y = f + g.
4) ==;
5) ===f´(x)+g´(x).
Итак, (f(x)+g(x))´= f´(x)+g´(x)
Например, (х2 +sinx)' =(x2)'+(sinx)' =2x+cosх. (икс в квадрате плюс синус икс штрих равно икс в квадрате штрих плюс синус икс штрих равно два икс плюс косинус икс).
Правило 2. Если функция у = f(x) имеет производную в точке х, то и функция y = kf(x) имеет производную в точке х, причем: (kf(x))'=kf'(x).
Т.е. постоянный множитель можно вынести за знак производной.
Докажем данное правило дифференцирования функции у = kf(x).
Воспользуемся алгоритмом отыскания производной.
1) Положим, ради удобства, kf(x) = h(x). Для фиксированного
значения х имеем: h(х) = kf(x).
2) В точке х+х имеем: h(x+x) = kf(x+Ax).
3) y=h(x+x)–h(x)=kf(x+x)–kf(x)= k(f(x+x)–f(x)) =kf
Итак, y=kf.
4) ==
5) ===kf´(x).
Получим (kf(x))' = kf'(x).
Например,
(5x2)´=5(x2)´=5·2x=10x; (пять икс в квадрате штрих равно пять, умноженное на икс в квадрате штрих равно пять, умноженное на два икс равно десять икс).
Правило 3. Если функции y=f(x) и у =g(x) имеют производную в точке х, то и их произведение имеет производную в точке х, причем:
(f(x) g(x))' = f '(x) g(x)+f(x) g´(x).
Т.е. производная произведения двух функций равна сумме двух слагаемых. Первое слагаемое есть произведение производной первой функции на вторую функцию, а второе слагаемое есть произведение первой функции на производную второй функции.
Например: ((2x+3)sinx)' =(2x+3)'sinx+(2x+3)(sinx)' =
=2sinx+(2x+3)cosx.
Правило 4. Если функции у = f(x) и y=g(x) имеют производную в точке х, причем в этой точке g(x)≠0, то и частное имеет производную в точке х, причем:
Например, == (икс в квадрате, деленное на пять минус четыре икс штрих равно десять икс минус четыре икс в квадрате, деленное на квадрат разности пяти и четырех икс).
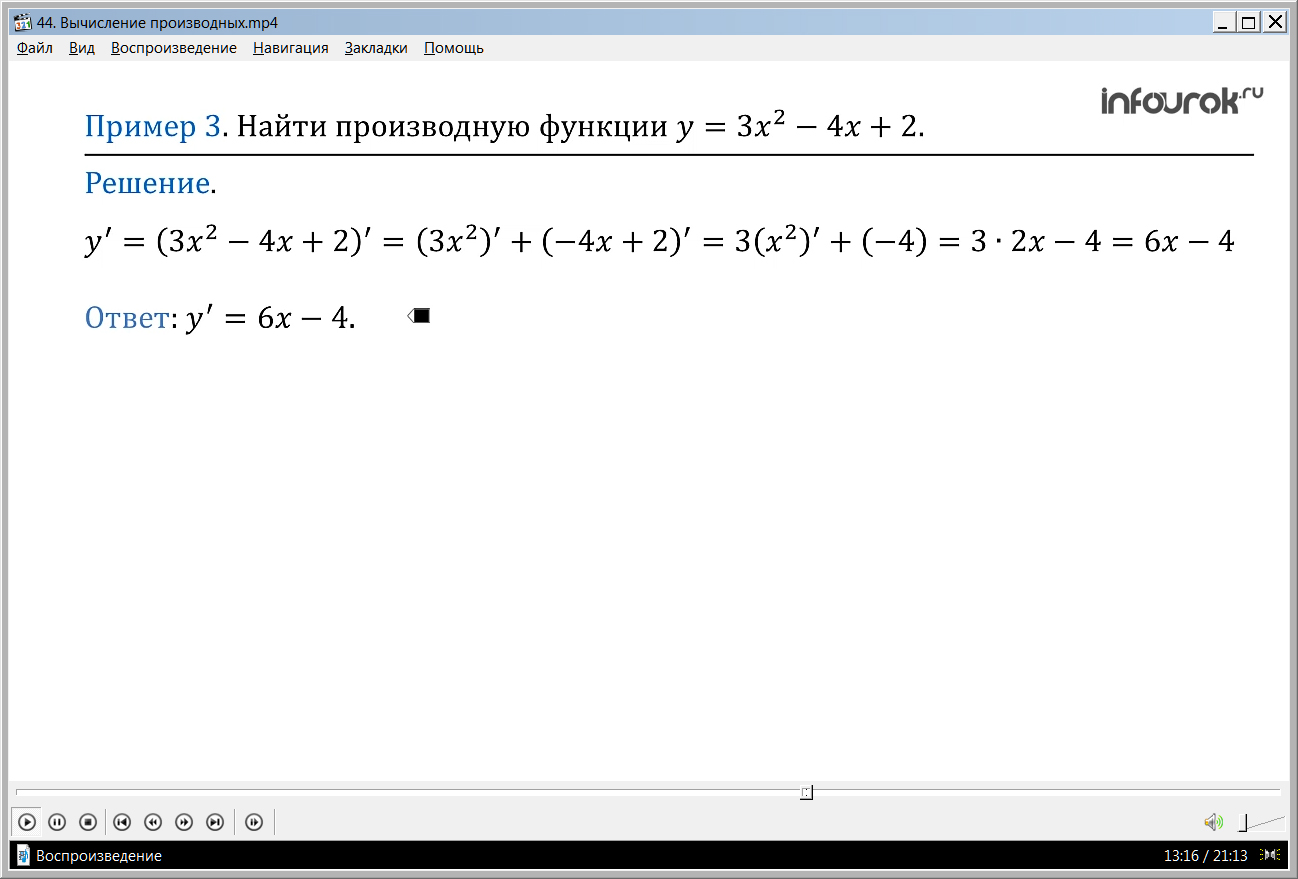
Пример 3. Найти производную функции у=3х2 –4х + 2.
Решение. Имеем:
у´=(3х2 –4х + 2)´=(3x2)´+(–4x+2)´= 3(x2)´+(–4)= 3·2x –4=6x –4
Мы воспользовались первым и вторым правилами, а также формулами
дифференцирования линейной функции у = –4х + 2 и функции у = х2.
Ответ: y'=6x–4.
Пример 4. Найти производные функций: а)у = х4; б)у = х5.
Решение: а) Представим х4 в виде х3 · х и применим правило дифференцирования произведения. Получим:
(х4)'=(х3· х)' =(х3)' ·х+ х3· (х)' = 3х2 ·х+ х3 ·1=4х3.
Итак, (х4)'=4х3.
б) Представим х5 в виде х4 · х и применим правило дифференцирования
произведения. Получим:
(х5)'=(х4·х)'=(х4)'· х+х4·(х)'=4х3· х + х4·1 = 5х4.
Итак, (х5)' = 5х4.
Ответ: а)(х4)'=4х3; б)(х5)' = 5х4.
А теперь сравним четыре формулы: две формулы, которые мы знали раньше, и те три формулы, которые мы вывели в примере 4. Смотрите:
х' = 1;
(х2)'=2х;
(х4)'=4х3;
(х5)'=5х4.
Возникает естественная гипотеза: для любого натурального показателя n справедлива формула дифференцирования:
(xn)'= nхn-1. (икс в энной штрих равно эн, умноженное на икс в степени эн минус один)
Пример 5. Найти точки, в которых касательная к графику функции
у = х3 –Зх + 2 параллельна оси х.
Решение. Имеем: у'=(х3 –3x + 2)'=3х2 –3.
Если касательная параллельна оси х, то ее угловой коэффициент равен нулю. Но, с другой стороны, угловой коэффициент касательной равен значению производной в абсциссе точки касания. Значит, нам нужно найти точки, в которых производная обращается в нуль. Имеем: Зх2 -3=0; находим: х1 =1,
х2 = –1.
Далее, f(1)=13–3·1+2=0
f(–1)=(–1)3–3·(–1)+2=4
Итак, касательная, проведенная к графику функции у = х3 –Зх + 2 в точке
(1; 0)или в точке (-1; 4), будет параллельна оси х. На рис. 1 дана геометрическая иллюстрация полученного результата — построен график функции у=х3–Зх+2. При этом мы учли, что f(–2)=0, т.е. график
пересекает ось абсцисс в точке х = –2.
Пример 6. Найти производные функций: а) у = tg х; б) у = ctgx.
Решение, а) Воспользуемся тем, что tgx = , и правилом дифференцирования частного. Получим: =====.
Таким образом, мы вывели еще одну формулу дифференцирования: = Понятно, что эта формула справедлива лишь при допустимых значениях х, т.е. при х≠.
б) Рассуждая аналогично,получим: =
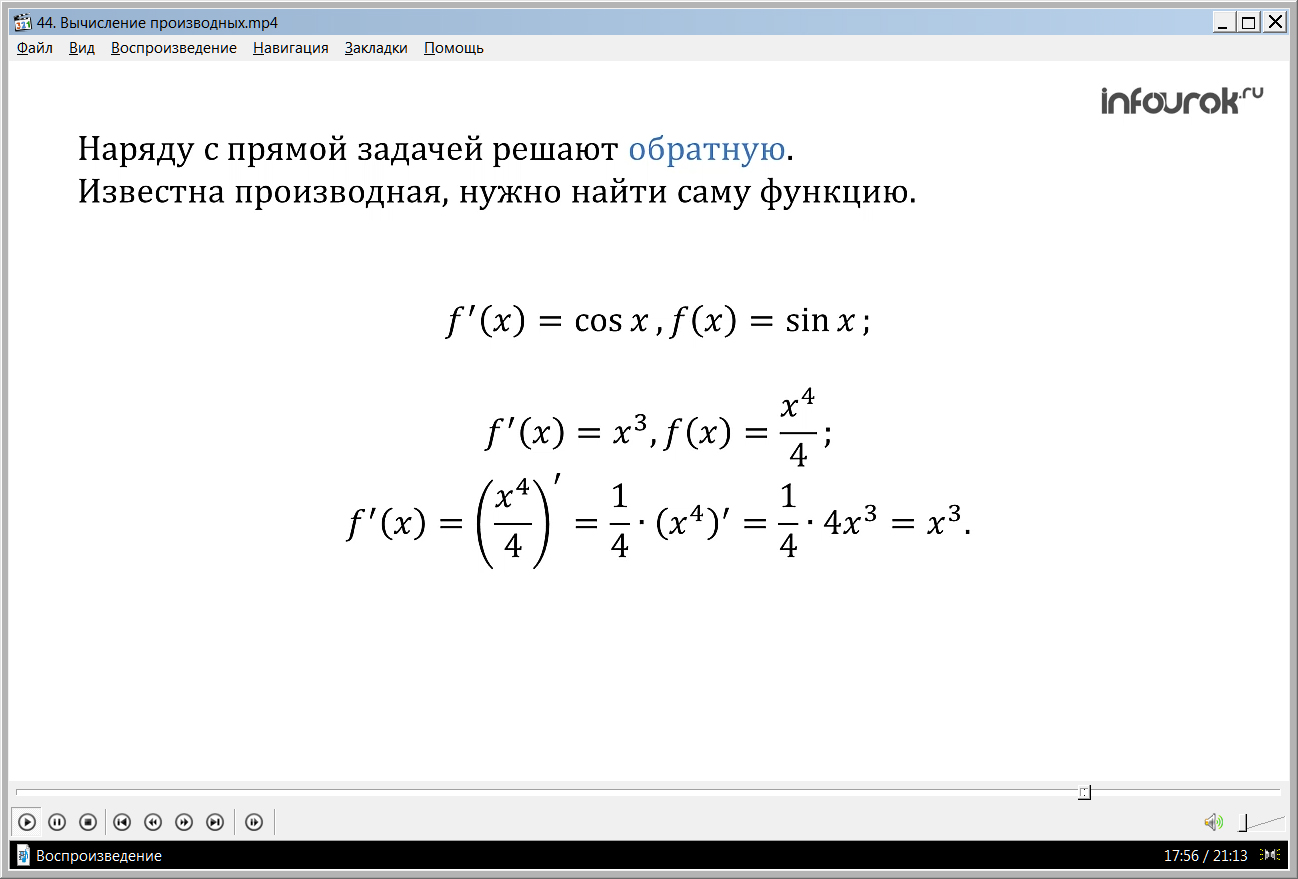
В математике наряду с прямой задачей часто решают обратную. До сих пор мы говорили о том, как по функции найти ее производную. Но часто бывает так, что известна производная, а найти нужно саму функцию. Если, например, известно, что f'(x) =cosx, то f(x) = sinx; в самом деле, производная от sinx равна cosx. Если известно, что f'(x) = x3, то нетрудно догадаться, что f(x)=; в самом деле, f´(x)= = = =.
3. Дифференцирование функции у = f(kx+m) (игрек равен эф от ка икс плюс эм).
Мы знаем, чему равны производные функций: у = хn(игрек равен икс в энной степени), y = sinx, y=cosx, y = tgx, у = . Нередко на практике приходится находить производные функций у = sin2x, y=cosи т.д. Возникает вопрос: если мы знаем, чему равна производная функции y = f(x), то как вычислить производную функции у = f(kx+m)?
С функцией y = sin2x можно поступить так. Известно, что sin2x = 2sinxcosx. Тогда: (sin2x)' =(2 sinxcosx)' =2((sinx)'cosx+sinx(cosx)') =
=2(cosxcosx+sinx(–sinx))=2(cos2x–sin2x)=2cos2x.
Здесь мы использовали правило вычисления производной произведения и правило вынесения постоянного множителя за знак производной, а также формулы синуса и косинуса двойного аргумента. То есть мы доказали, что (sin2x)'=2cos2x. (синус два икс штрих равно два косинус два икс)
В формулах sin5x, sin–2x? sinkx: аргументом является не x, а kx.
И тогда применяем известную формулу дифференцирования только появляется дополнительный множитель, равный коэффициенту k при x. Например, справедливы следующие формулы:
(cos(–7x))' = 7∙ sin(–7x);
(sinx)'=cosx;
(( - х + 1)5)′= - 1∙ 5( - х +1)4= - 5( - х +1)4
Справедлива следующая теорема.
Теорема. Производная функции у= f(kx+m) вычисляется по формуле
(f(kx+m))'=kf '(kx+m). (эф от ка икс плюс эм штрих равно кА, умноженное на эф штрих от ка икс плюс эм).
Пример 7. Найти значение производной функции y = f(x), где f(x)=, в точке х = 5. (эф от икс равно корень квадратный из восемь минус одна целая пятнадцать сотых икс)
Решение. Сначала найдем производную в произвольной точке х. Известно, что ()'=. По этой формуле найдем интересующую нас производную, но при этом учтем два обстоятельства: 1) под знаком корня напишем не х, а
8 –1,15х; 2) укажем дополнительный множитель, равный –1,15 – это коэффициент при х. Таким образом, ()'=.
Чтобы вычислить f(1), в полученное выражение подставим х = 5:
f´(5)
Ответ: f´(5)
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 20726 |
| Номер материала | 867 |