
Презентация "Определение степени с натуральным показателем"

Краткое описание документа:
Главная прелесть математики в том, чтобы находить красивые решения. Тот, кто это понимает сразу,начинает любить предмет по-особому. Именно эта наука подходит к решению различного рода задачмаксимально рационально, чтобы человек мог затрачивать минимум личного времени, но при этом несовершать ошибки при сложных вычислениях. Можно запросто запомнить несколько действий и тогдасправляешься со всем гораздо быстрее и с удовольствием. Более того, всё элементарно простопросчитывается в уме, и нет необходимости в использовании калькулятора. Одно из удовольствий – эторабота со степенями.
Если повторно умножить одно и то же число, то его можно написать в степени. Например:
4*4*4*4*4*4=4^6
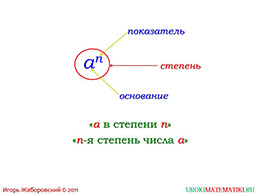
То есть мы получили четыре в степени шесть, где четыре – это основание степени, а шесть – еёпоказатель.


слайды 1-2 (Тема презентации "Определение степени с наутральным показателем", пример)
А что если возвести в степень m*m*m*m*m*m*m, 5*5*5*c*c*c, ppkk+pppk-pkkk?
В первом случае всё довольно просто, мы получаем «m» в степени шесть. Далее чуть сложнее, но видно,что пять повторяется три раза, впрочем, как и «с», поэтому выйдет 5с в степени три. Последний пример,как говориться, со звёздочкой, выйдет сумма следующих произведений: «p» в степени два на «k» встепени два, «p» в степени три на «k», а далее из полученного выражения вычитаем произведение «p» и«k» в степени три.
Если число возведено в первую степень, то это лишь означает, что оно равняется самому себе. Тополучаем: 18^1=18, 198^1=198,392^1=392


слайды 3-4 (примеры, определение степени)
Вторую степень называют квадратом, то есть число три в степени два может также звучать как три вквадрате. Третья же степень называется кубом, поэтому, когда любое число (например, четыре), возведёмв третью степень, то получим число в кубе (например, четыре в кубе).
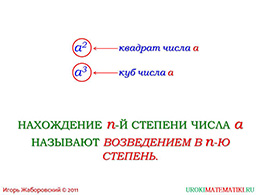
слайды 5-6 (примеры, определение возведения в степень)
Работая с положительными числами, мы возводим основание в любую степень (четную или нечётную) ивсё равно получаем такое же положительное основание. Здесь всё просто, но стоит обратить внимание навыражения с неположительными числами. При работе с отрицательным основанием есть ряд особенностей.Представим, что у нас есть отрицательное число, которое необходимо возвести в чётный показатель. Вданном случае число становится положительным. К примеру: (-9)^2=81


слайд 7-8 (примеры)
Если же отрицательный основатель надо возвести в отрицательную степень, то основание знак минусане теряет. К примеру: (-3)^3=-27
Отдельно дела обстоят при работе с нулем. Когда возводим нуль в абсолютно любую степень, то мы всёравно получим нуль, ведь мы просто несколько раз перемножаем его на самого себя. Обратим внимание:0^7=0

слайды 9-10 (пример, калькулятор)
Один из достаточно сложных примеров – это возвести в шестую степень нецелое число (например,шесть целых одну десятую возвести в степень семь). В таком случае понадобиться калькулятор для того,чтобы совершить повторные действия произведения или же на передовых моделях есть возможностьвозведения в степень (для этого стоит найти специальную кнопку).
Теперь можно смело переходить на задания очень сложного типа или, как говориться, задания с двумязвёздочками. Например:


слайды 11-12 (примеры)
Данный пример можно разделить на четыре действий. Во-первых, возведём в квадрат минус шесть иполучим тридцать шесть. Во-вторых, минус два в пятой степени равняется минус тридцати двум(отрицательность сохраняется, так как степень нечётная). В-третьих, шестьдесят четыре делим на минустридцать четыре, и выходит минус два. В-четвёртых, мы находим сумму минус тридцать шесть и минус дваи получаем минус тридцать восемь. Соответственно ответ этому сложному пример равняется минустридцать восемь. При решении стоит запомнить, что основанием может быть любое число, а вот показательдолжен быть натуральным числом.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4071 |
| Номер материала | 184 |