
Презентация "График функции"

Краткое описание документа:
В математике существенно множество закономерностей, в этом уроке речь пойдёт об одном из важнейших понятий, о функции. То, что привлекает внимание школьников с седьмого класса или функция - так называемый «закон», по которому каждому элементу определённого множества подставляется другой элемент множества. Независимой переменной выступает «х» (или же аргумент), а «у» напрямую зависит от значений аргумента и называется значением функцией или просто функцией. Именно в функции видна зависимость одной переменной от значений другой.
Стоит объяснить, что многие области знаний зависят именно от функций (кроме математики, это и физика, и химия, и биология), потому что они пытаются понять взаимосвязь объектов и данных. Из материала понадобится интерактивная доска или распечатанный раздаточный материал.


слайды 1-2 (Тема презентации "График функции", пример)
Задачей учителя будет систематизировать теоретические знания, и закрепить понятие «график функции». Сразу презентация начинается с примера функции, где «у» называем функцией от переменной «х», которая задаётся определённой формулой. Главная задача – использование наглядного примера, чтобы заинтересовывать учащихся, поэтому нарисуем таблицу. Находим, при каких значениях «х» функция возможна (видим, что функция реальна при «х» от минус двух до плюс шести). В формате таблицы подбираем все значения функции в возможном промежутке.
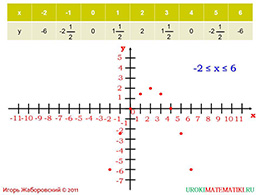
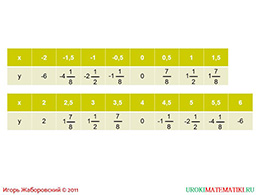
слайды 3-4 (примеры)
Полученные результаты наносим на оси абсцисс и ординат. Теперь видно, что фигура – нисходящая парабола, что изначально можно было определить по формату функции (объяснить почему). Она имеет коническое сечение, а ось проходит через точку с координатой два, вершина же отмечена в координатах (2; 2). Однако данных сведений не достаточно для того, чтобы корректно нарисовать фигуру, необходимо рассмотреть каждую её часть в промежутке от минус двух до двух и от двух до шести.
Вновь в табличной форме находим значения функции при половинчатых данных. На данном этапе важно не давать возможность использовать калькулятор школьникам, а вовлечь их в процесс просчёта дробей. Например, можно каждому отдельному ученику задать определённый показатель «у» при данном значении «х».
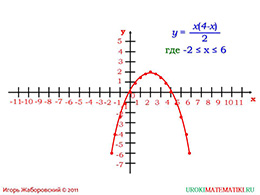

слайды 5-6 (пример, определение графика функции)
Все полученные результаты доносим на график и уже уверенно можем видеть, как выглядит заданная функция. После проделанных вычислений важно сказать определение «графика функции», уточнив у школьников, где же значения аргумента, а где – значения функции. Постарайтесь максимально вовлечь всех в разбор определения и попросить кого-то из присутствующих объяснить его своими словами.
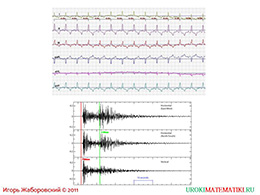
слайды 7-8 (примеры)
За теорией следует закрепить материал более живыми примерами: покажите следующие две картинки детям и попросите их догадаться, что именно представляет каждый из графиков. Главное – контролировать поток детской фантазии, чтобы она не понесла всех в хаотичное направление. Задайте следующие вопросы: насколько диаграммы подобны и стабильны? Имеют ли они какое-то сечение?
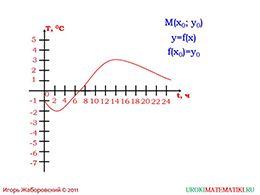
Показав следующий график школьникам, стоит обратить их внимание на названиях осей. Почему на оси абсцисс цифра доходит до 24х? Подтвердите, что это отношение суточного времени от температуры. Может ли кто-то проанализировать, как изменялась погода в течение суток? Где виден максимум и минимум температур?
слайд 9 (пример)
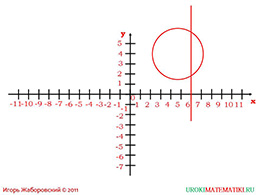
Напоследок – задание со звёздочкой. Спросите: есть ли сечение у функции? Какие ассоциации вызывает данная фигура? Помнит ли кто формулу круга? Далее попросите каждого перерисовать данный график себе в тетрадь и разобрать его дома с родителями. Данное задание поможет воспитать в учащихся желание к познанию и организует синергию с родителями.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4331 |
| Номер материала | 203 |