
Презентация "Взаимное расположение графиков линейных функций"

Краткое описание документа:
Изучив материал по построению графиков линейных функций, можно уже переходить к другой теме, касающейся взаимного расположения подобных графиков. С помощью этой презентации учащиеся должны понять, каким образом могут располагаться на одной и той же оси координат два графика линейных функций по отношению друг к другу.


слайды 1-2 (Тема презентации "Взаимное расположение графиков линейных функций", пример)
Первый слайд презентации напоминает о том, что в случае, если коэффициент x будет равен нулю, то линейная функция станет равна значению коэффициента b. Для школьников стоит повторить, что при соблюдении данного условия прямая графика будет проходить только по оси Y. Также область значений подобного графика будет напрямую зависеть от значения коэффициента b.
слайды 3-4 (примеры)
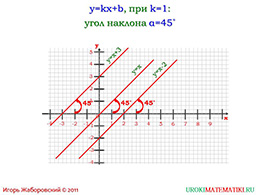
Следующий слайд презентации говорит о том, что коэффициент k важен для графика не только тем, что обеспечивает пересечение графика через ось X, но и задает определенный угол наклона прямой по отношению к оси координат. В приведенном примере коэффициент k равен числу 1, что позволяет получить угол наклона в 45 градусов.
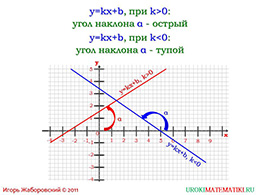
Но у коэффициента k есть еще одна важная миссия в построении графика: в зависимости от того является ли коэффициент k по своему значению больше или же меньше нуля, угол наклона может оказаться острым или, напротив, тупым. На наглядном примере в презентации показан, как первый вариант, так и второй вариант. При этом обе прямые между собой пересекаются в одной точке.

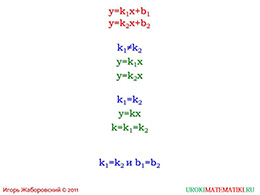
слайды 5-6 (примеры)
Из-за того, что коэффициент k обладает подобными функциями при построении графиков, его назвали угловым коэффициентом прямой или, проще говоря, графика.
Чтобы учащиеся смогли усвоить зависимость расположения двух графиков от значения углового коэффициента, на данном слайде приведен пример, в котором участвуют две линейные функции с двумя угловыми коэффициентами. В первом случае один коэффициент k не равен другому коэффициенту k, что, естественно, приводит к построению различных графиков, а также разным углам по отношению к осям. Во втором же случае оба угловых коэффициента равны, что говорит о том, что линейные функции между собой равны. Это также касается и их коэффициентов b и b1.

слайды 7-8 (пример)
Исходя из этих примеров, школьники должны сделать очень важный вывод. В случае если угловые коэффициенты двух прямых различны по отношению друг к другу, то эти прямые должны пересечься между собой. Если же коэффициенты k, задающие углы своим прямым, одинаковы, то обе прямые будут обязательно параллельны, а значит и пересечение между ними невозможно.
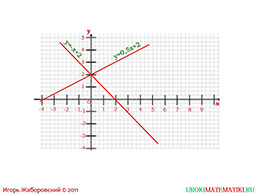
После того, как придет понимание этого утверждения, необходимо наглядно его закрепить в сознании учащихся. Первый пример как раз относится к первому случаю, то есть когда угловые коэффициенты различны между собой, а прямые имеют возможность пересекаться.
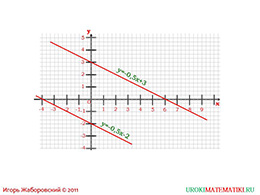

слайды 9-10 (примеры)
Во втором примере школьники увидят, что действительно при равных значениях коэффициентов k прямые окажутся параллельными, и не будут иметь общей точки пересечения.
После того, как теоритический материал будет донесен до учеников 7-го класса, презентацией предлагается решить в качестве примера одну задачу по определению координат общей точки пересечения двух разных линейных функций. Данный пример может быть закреплен еще несколькими примерами по усмотрению учителя.
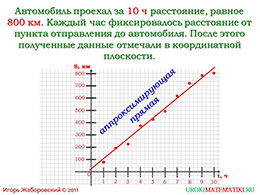
слайды 11 (пример)
После практического закрепления полученного материала учителем должно быть объяснено, что собой представляет такое явление, «аппроксимирующая прямая». Она строиться в том случае, когда вычисленные координаты принимают вид кривой, а не прямой, поэтому построить график обычным способом не представляется возможным. На слайде презентации приведен как раз пример построения аппроксимирующей прямой. На этом тема урока, а соответственно презентация, подошла к своему концу. Если у школьников возникли какие-либо вопросы, то они задают их учителю. При желании ученики 7-го класса могут повторить пройденный материал по этой теме самостоятельно с помощью этой же презентации.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 3871 |
| Номер материала | 212 |