
Урок "График функции"

Краткое описание документа:
Все множество чисел, как положительных, так и отрицательных, можно представить не только в виде числового линейного набора, но и при помощи Декартовой системы координат. Более того – многие частные множества или рабочие участки множеств проще представить именно в графическом виде.
Напомним, что Декартова система представлена двумя осями: абсцисс и ординат. Ось абсцисс проходит горизонтально, отображая первое множество всех действительных реальных чисел. Во многих случаях для графического представления неравенств, к примеру, достаточно одной оси абсцисс. Но так как функция представляет собой связанную пару множеств, то для её графика необходимо ввести ось второго множества – ординат. Вторая ось проходит перпендикулярно первой, образуя общую координатную сетку. Ноль является общим универсальным элементом, объединяя обе оси.
Ось абсцисс обозначают как х и связывают множество значений на ней со множеством аргументов функции. Ось ординат обозначается как у, и множество её значений связано со множеством значений самой функции. Можно ещё выразить эти же понятия так: на оси абсцисс лежит область определения функции, а на оси ординат – область значений функции.
После теоретической базы для графического построения математической зависимости можно построить график. Для этого, в общем случае, используют следующий алгоритм. Для любой функции у = f(х):
- Определяем область, в которой нужно отобразить функцию графически. Большинство функций имеют бесконечные (непрерывные) области значений и аргументов, поэтому необходимо выбрать интересующий участок в виде алгебраического интервала аргументов: например, все значения х от –а до +b;
- Создаем таблицу соответствий. Для этого выписываем все аргументы, входящие в интервал (как правило, используются все целые числа), и вычисляем по функции f значения переменной у для каждого х, записывая все данные в таблицу;
- На основании таблицы отмечаем точки на декартовой системе координат, используя ось абсцисс для аргументов и ось ординат для значений функции;
- Соединяем точки в общую графическую кривую – график готов.
Предположим, нам необходимо построить график функции:
у = х2
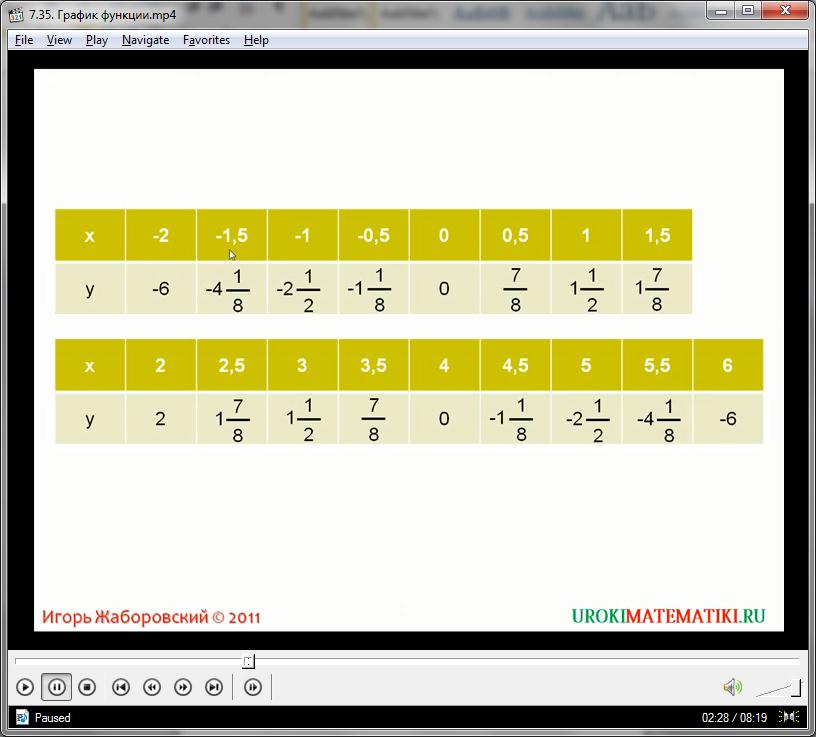
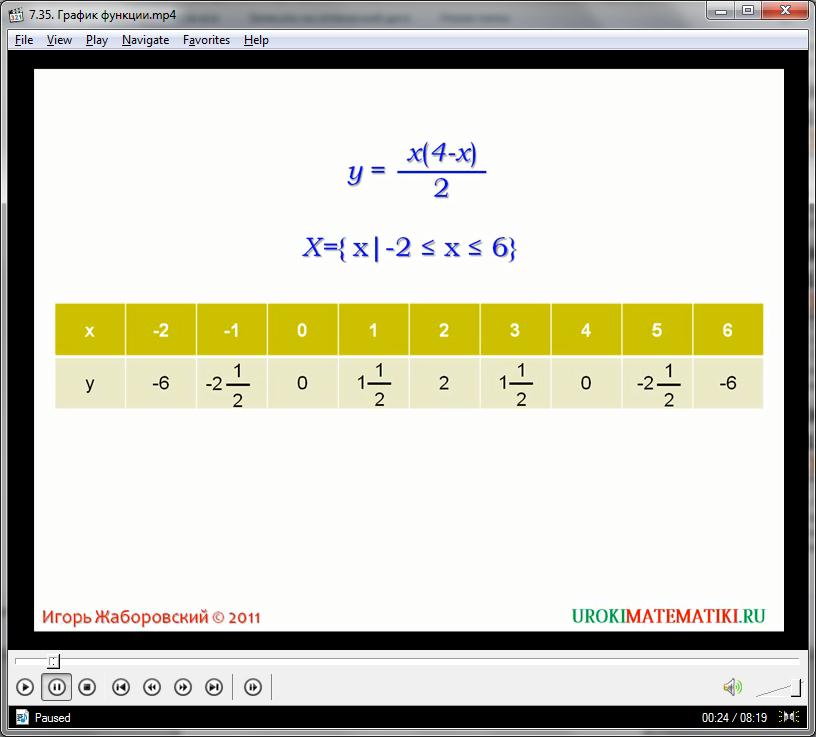
Определим график нашей функции на интервале от -2 до 2:
Х = -2 (больше или равно) х (больше или равно) 2
Создаем таблицу соответствий, рассчитывая значения у путем возведения в квадрат аргументов х, взятых в заданном интервале:
При х = -2 : у = (-2)2 = 4
При х = -1 : у = (-1)2 = 1
При х = 0 : у = (0)2 = 0
При х = 1 : у = (1)2 = 1
При х = 2 : у = (2)2 = 4
На основании таблицы строим график. Как можно наблюдать в нашем видео, график этой функции представляет собой параболу с вершиной в точке (0, 0).
Графики функций широко распространены – и в научно-технических отраслях, и в повседневной жизни. Это обусловлено тем, что математические зависимости – важнейший фундамент для множества различных формул, при помощи которых описываются тысячи процессов. Например, зависимость сокращения сердечной мышцы от времени передается специфической формулой и соответствующим графиком – кардиограммой. Колебания поверхности земли, зависимые от времени, передаются графически сейсмограммой.
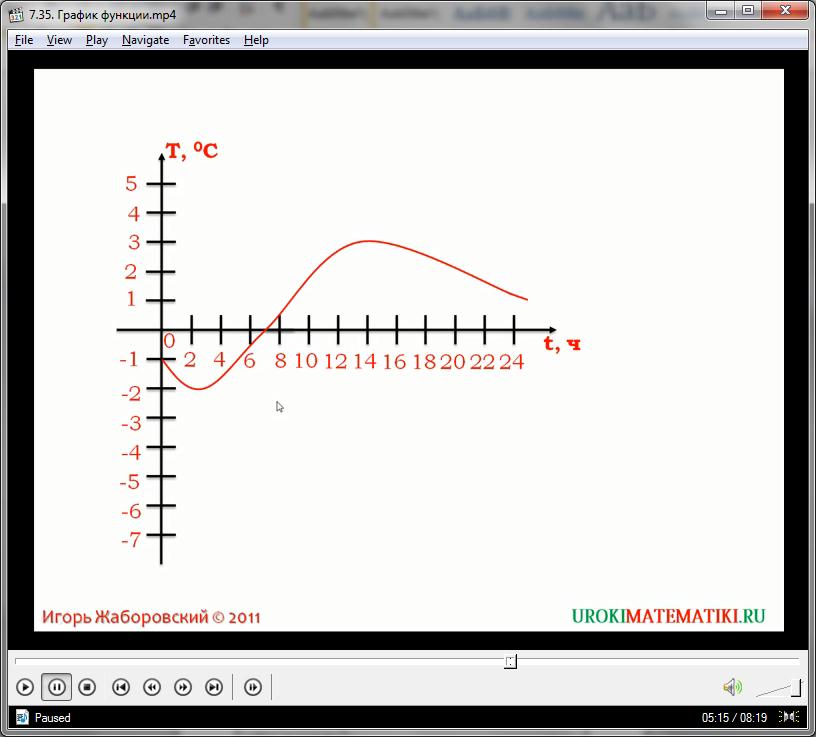
Многие графические представления функций служат для быстрого нахождения значения функции по заданному аргументу. В тривиальной практике довольно часто случается и обратное: по заданному значению ищется аргумент функции. Следует понимать, что любая функция – это равенство, и она действительна в любом направлении (в большинстве случаев).
Например, на видео представлен график зависимости температуры воздуха от времени суток. При этом значения времени отложены на оси абсцисс, формируя множество аргументов от 1 до 24 (график рассчитан на интервал в одни сутки). Множество значений температуры обозначены на оси у – причем как в положительной, так и в отрицательной части. Если нам нужно узнать по графику, какая температура была в 8 часов утра, то можно провести перпендикуляр от оси х, в точке (8, у), и посмотреть, где он пересекает график. Легко заметить, что точка А на графике имеет координаты (8, 1) и соответствует такому выражению: при аргументе, равном 8, функция приобретает значение, равное единице. Иначе говоря, в 8 часов утра температура воздуха была +1.
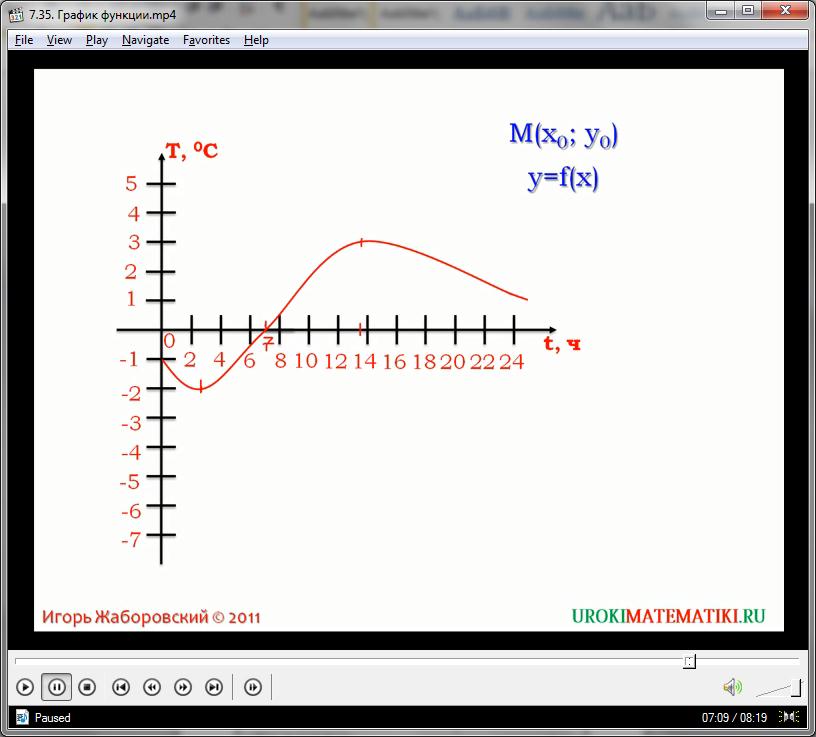
Многие функции, используемые на практике (например, те же сейсмограммы), являются довольно сложными в аналитическом линейном виде. И графическое представление, в таком случае, не только более наглядное, но и гораздо более практичное. С технической точки зрения, большинство практических зависимостей проще отобразить именно графиком, чем проводить сложные математические расчеты по выводу линейной формулы.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6212 |
| Номер материала | 462 |