
Презентация "Линейное уравнение с двумя переменными и его график

Краткое описание документа:
На данном уроке учащиеся узнают, что такое линейное уравнение с двумя переменными, а также научатся строить его график. Для начала проведите блиц-опрос о том, что такое уравнение, и чем оно отличается от неравенства? Далее попросите привести пример уравнения с одной и двумя переменными. В математике мы достаточно часто видим уравнения с двумя переменными, поэтому необходимо остановиться на теме подробнее.


слайды 1-2 (Тема презентации "Линейное уравнение с двумя переменными и его график", определение графика уравнения с двумя переменными)
Теперь смело переходите к теоретическому материалу данного урока: дайте определение графику уравнения с двумя переменными. Вот ученики понимают, что именно график помогает найти множество возможных значений для уравнения.

слайды 3-4 (примеры, определение линейного уравнения с двумя переменными)
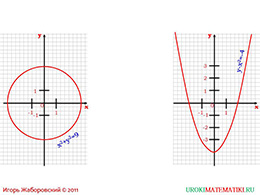
Дети уже должны знать, что такое система координат. Попросите учеников её нарисовать, изображая следующие графики: сумма «х» в квадрате и «у» в квадрате равняется девяти, а также разность «у» и «х» в квадрате равна минус четырём. Таким образом, вы напоминаете, что уравнение с двумя переменными может иметь как бесконечное множество вариантов (второй пример и график справа), или одно значение (первый пример и график слева).
Приведём несколько примеров линейных уравнений с двумя переменными, чтобы дать чёткое определение. Сделайте акцент на том, что «a», «b» и «c» - некоторые числа в данном случае, а «х» и «у» - переменные. Более того, «a» и «b» не могут быть равны нулю, потому что они составляют часть произведения с одной из переменной. Решением уравнения с двумя переменными будет та пара значений, которая делает уравнение верным равенством. Любая пара чисел на плоскости изображается какой-то точкой. У данных примеров много уравнений, то есть много пар.
слайды 5-6 (примеры)
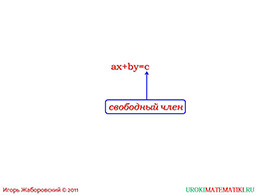
Повторим вновь, «a» и «b» не могут быть равны нулю, потому что они связанны с переменными. Однако есть третий член или «с», который является свободным и может собой представлять любое значение. Главное, опять же, чтобы поставленная пара значений делало уравнение верно числовым.
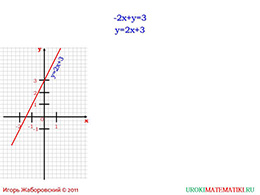
Изобразим наш пример на графике, где есть какие-то две точки на плоскости, через которые проходит прямая. Мы точно знаем, что это прямая, потому что такой формат уравнения говорит о том, что уравнение линейное.

слайды 7-8 (примеры)
Давайте наглядно к уравнению подставим ноль вместо «а» или «b». В таком случае мы видим, что «х» равняется двум, а «у» может быть любым числом. Делаем следующий вывод.
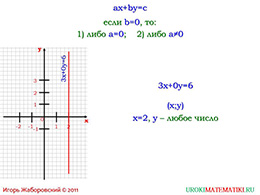
Графиком в данном случае является прямая, параллельная одной из осей. Мы также можем сделать вывод, что графиком является пустое множество, когда в линейном уравнении коэффициенты при заданных переменных представляют собой ноль. А что если не только коэффициенты, но и свободный член равен нулю? Тогда графиком нашего уравнения является плоскость. Необходимо рассмотреть ряд примеров.
слайды 9-10 (примеры)
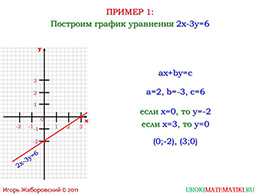
Для начала рассмотрим уравнение, где разность двух «х» и трех «у» равна шести. Мы видим, что перед переменными у нас стоит два и минус три, а свободный член равен шести. Представим, что «х» равен нулю и трём. Тогда мы смело находим значение «у» и получаем в итоге две точки, через которые можем провести прямую. Данная прямая будет графиком линейного уравнения.
Для того чтобы понять, как выглядит график линейной функции достаточно знать значение двух точек, так как прямая будет проходить именно через них.
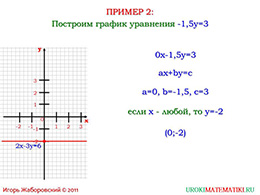
Во втором примере разделим изначальное уравнение на два, тогда получим, что один из коэффициентов при переменной равняется нулю, а графиком функции выступает прямая, при которой «х» имеет любое значение, а «у» равна минус двум.
слайд 11 (пример)
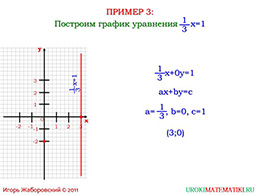
Рассмотрим последний пример: попросите учащихся разделить изначальное уравнение на коэффициент перед «у». Тогда мы получаем, что график уравнения будет параллелен оси ординат, и проходить через точку три на оси абсцисс.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 5560 |
| Номер материала | 216 |