
Презентация "Возведение одночлена в степень"

Краткое описание документа:
Урок «Возведение одночлена в степень» построен таким образом, чтобы ученики могли с легкостью усвоить новый материал и использовать полученные знания на практике. Здесь ученикам понадобятся уже освоенный ими материал – операции с дробями, умножение одночленов и их преобразование. Целью урока является систематизация знаний по теме «Умножение одночленов», а также по теме «Возведение одночлена в степень». Ученики должны применять навыки формирования общения, сравнения, закреплять первично полученные знания.


слайды 1-2 (Тема презентации "Возведение одночлена в степень", пример)
Для начала рассматривается одночлен, который записан в скобках под общим знаком степени. Используя преобразования и правило умножения одночлена на одночлен в конечном итоге получили одночлен стандартного вида, в котором каждая переменная возведена в степень. Отсюда получаем правило возведения одночлена в степень – для того, чтобы возвести одночлен в степень, необходимо каждый множитель одночлена возвести в степень. В качестве доказательства данного правила показан пример возведения многочлена ab в степень n, где n – натуральное число. Ученикам напоминается, что одночленами не являются выражения, которые являются суммой, разницей или частным переменных и чисел. Напоминается также о таких понятиях, как подобные одночлены – одночлены, имеющие одинаковые буквенные выражения, а привести подобные члены – значит сложить их числовые коэффициенты, а результат умножить на общий буквенный множитель.

слайды 3-4 (примеры)
Чтобы ученикам стало более понятно, как применять это правило на практике, рассматриваются ещё несколько примеров более сложных одночленов (с большим количеством множителей) и возведение их в степень.


слайды 5-6 (примеры)
После рассмотрения правила возведения одночлена в степень само собой возникает вопрос о том, как возводить в степень произведение одночленов. Все очень просто. Для этого необходимо воспользоваться правилом возведения произведения одночленов в степень, которое звучит следующим образом: для того чтобы возвести в степень произведение одночленов, необходимо каждый множитель возвести в степень, а полученные результаты перемножить между собой.


слайды 7-8 (примеры)
Ученикам показывается конкретный пример и представляется запись этого правила в общем виде.
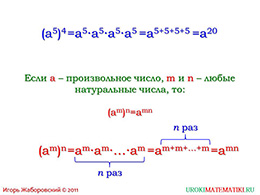
Далее, ученикам предлагается рассмотреть и изучить ещё одно правило, касающееся одночленов. Возникают ситуации, когда необходимо возвести в степень одночлен, который уже находится под степенью. В этой ситуации на помощь придет следующее правило: для возведения степени в степень одночлена, необходимо основание оставить таким же как оно и было, а степенные показатели перемножить.
Если возникает необходимость возвести в степень дробь, необходимо применить ещё одно правило, касающееся дробей: для возведения в степень дроби, необходимо отдельно возвести в степень числитель, отдельно – знаменатель, а ответ записать под общим знаком дроби.

слайд 9 (пример)
Для закрепления знаний на практике ученикам предлагается рассмотреть несколько примеров возведения одночлена в степень с их подробным объяснением. Так, на первом примере ученики могут рассмотреть, как возводить в шестую степень многочлен, содержащий числовой множитель и две буквенные переменные. Во втором примере можно увидеть, как возводили одночлен в третью степень.
В заключении урока ученикам показывается запись основных правил – возведение в степень произведения и возведения в степени в степень, в общем виде. Делаются выводы и подводятся итоги проведения урока и полученных новых знаний, учитель делает небольшой опрос и отвечает на вопросы, которые возникли у учеников.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 3835 |
| Номер материала | 224 |