
Урок "Определение степени с натуральным показателем"

Краткое описание документа:
Степень – одно из важнейших математических понятий. В элементарном отношении степень – это показатель перемножения числа на самого себя. Например, у нас есть число 5. Умножим его на свое же значение 3 раза:
5*5*5 = 125
Левую часть равенства можно записать короче, оставив пятерку на прежнем месте, а количество перемноженных элементов представить в верхнем индексе справа:
5*5*5 = (5)3
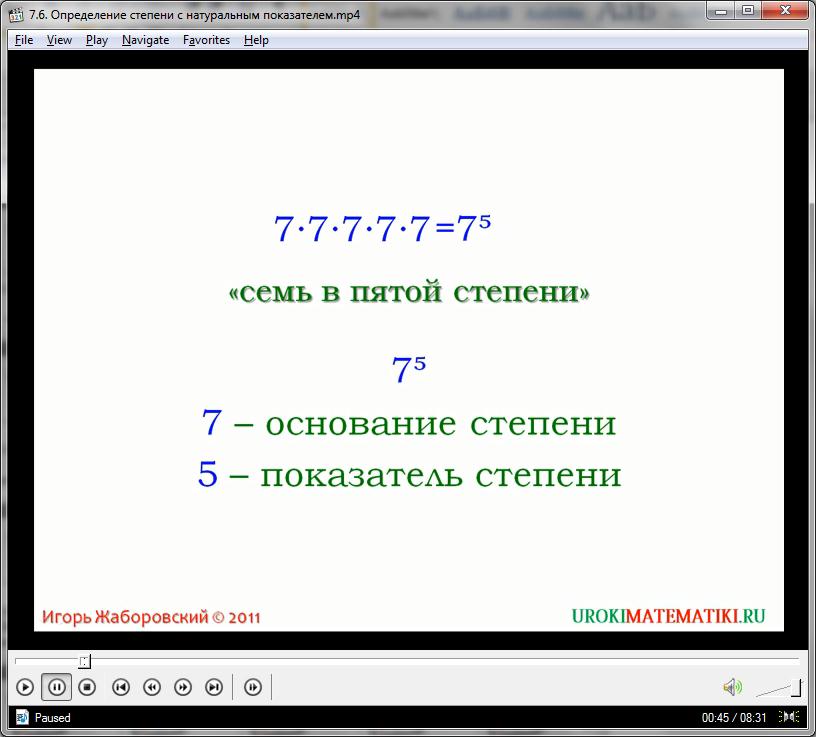
Таким образом, степень показывает нам, сколько чисел под степенью нужно перемножить, что бы получилось правильное выражение. Важно понимать, что значение степени характеризует именно количество элементов, участвующих в умножении, а не количество процессов произведения. Иными словами, (5)3 означает, что нужно взять три (по показателю степени) числа «5» и перемножить их друг на друга. Подстепенное выражение именуют основанием степени, а само число, которое указывает на количество множителей – показателем степени.
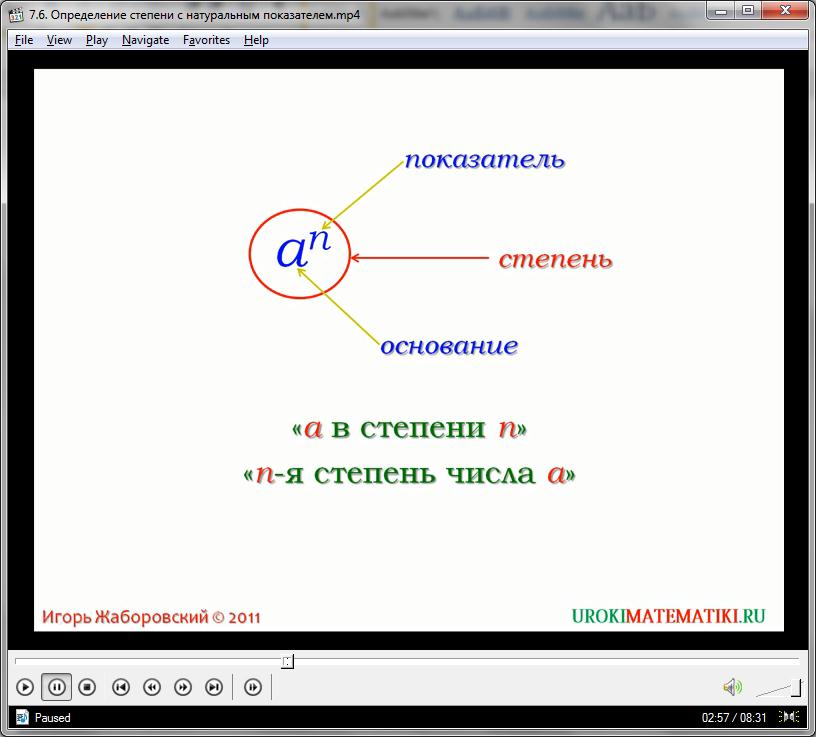
Возведением в степень некоего основания называют процесс перемножения этого основания на само себя в заданном показателем степени, количестве.
Показатель степени может быть любым натуральным числом. Если он равен единице, то считается, что для умножения основание взято лишь один раз, то есть любое основание в степени, равной единице, будет равно самому себе:
(а)1 = а* = а
Для некоторых степеней существуют специальные названия, происходящие из геометрических определений. Так, вторую степень называют квадратом, а третью – кубом числа.
Для практического примера, возведем число (-3) в квадрат и куб:
(-3)2 = (-3)*(-3) = 9
(-3)3 = (-3)*(-3)*(-3) = -27
Из базовых свойств умножения следуют некоторые правила степеней, например:
1. При умножении нуля на ноль получается всегда ноль вне зависимости от количества процессов умножения. Следовательно, ноль в любой степени будет равен нулю;
2. При умножении любых положительных чисел получаются только положительные числа, поэтому любая степень с положительным основанием дает положительное значение числа;
3. При умножении двух отрицательных чисел получается положительное, а при умножении положительного на отрицательное – отрицательное. Отсюда вытекает весьма важное свойство степеней, которое делит все степенные показатели на две большие группы – четные и нечетные. При четной степени, и при основании с любым знаком, всегда будет получаться положительное значение всего выражения. Нечетная степень с отрицательным основанием дает отрицательное выражение, с положительным – положительное. Иными словами, нечетная степень всегда сохраняет знак основания.
Четность степенного показателя имеет очень важное значение в линейной алгебре, так как играет большую роль для многих определений, с которыми мы познакомимся в дальнейших видеоуроках.
При решении различных упражнений, важно соблюдать порядок действий – например, произведение по рангу равно делению, но стоит выше вычитания и суммирования. Возведение в степень является ещё более приоритетным: нельзя проводить какие-либо действия с основанием, не выполнив степенного перемножения. Найдем значение выражения:
(-6)2 + 64/(-2)5
Сначала возводим в степень (-6) и (-2), памятуя о том, что четная степень (2) оставляет только положительные значения, а нечетная (-5) сохраняет знак основания:
(-6)2 = (-6)*(-6) = 36
(-2)5 = (-2)*(-2)*(-2)* (-2)* (-2) = -32
Подставляем готовые значения, решаем выражение:
(-6)2 + 64/(-2)5 = 36 + 64/(-32) = 34
На применении правил четности и нечетности степеней можно решать и более сложные примеры. Найдем все значения выражения:
5(-1)(n +1) + 2
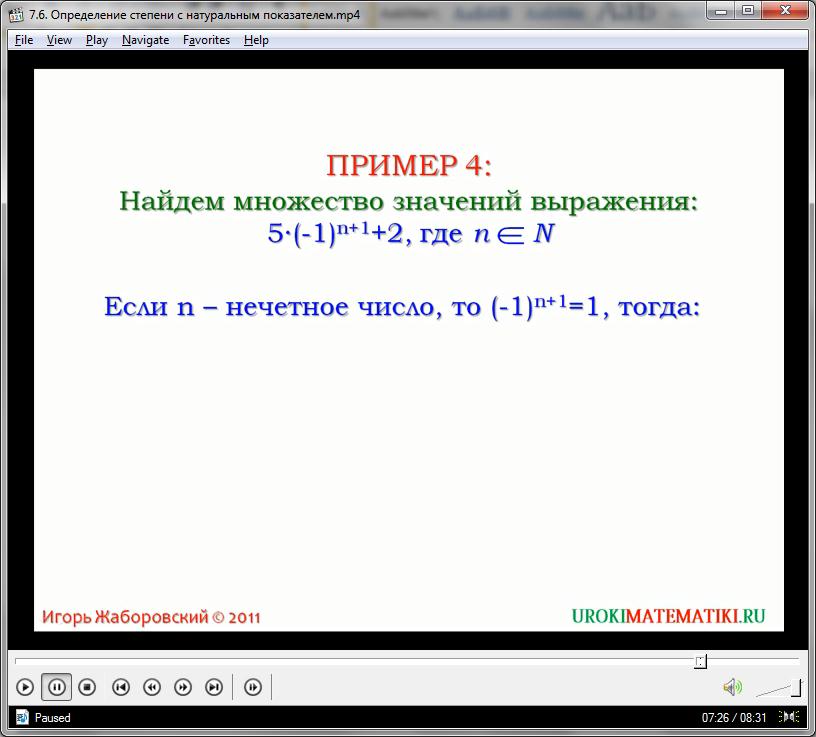
Теоретически, данное выражение может иметь два значения, одно из которых соответствует четной, а другое – нечетной степеням. Основание (-1) при возведении в любую натуральную степень может иметь вариации только по знаку, а не по основному значению. Причем знак итогового числа будет зависеть от четности степени.
Итак, пусть n – четное число, тогда (n + 1) – нечетное, (-1)(n + 1) равно, в таком случае, -1, а все выражение:
5(-1) + 2 = -3
Если же n нечетное, то (n + 1) будет четным, а (-1)(n + 1) положительным числом, то есть, будет равно единице. Тогда все выражение равно:
5(1) + 2 = 7
Значит, наше выражение может иметь только два значения – (-3), если n четная, и (7), если n нечетная.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5143 |
| Номер материала | 1102 |