
Презентация "Решение квадратных неравенств" Часть 1

Краткое описание документа:
Неравенства в курсе алгебры занимают важное место. Им отведена не малая часть в содержании всего курса алгебры. Благодаря умениям решать разного рода неравенства, во многих других науках можно иметь успехи. Чтобы материал, который преподается на уроке, лучше усваивался, рекомендуется использовать разную наглядность, в том числе и презентации.

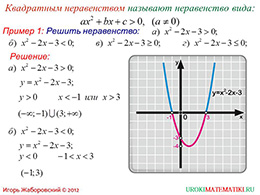
слайды 1-2 (Тема презентации "Решение квадратных неравенств. Часть 1", пример)
Данная презентация предназначена для урока объяснения нового материала, который входит в систему уроков по разделу «Неравенства». Прежде чем приступать к изучению данной темы «Решение квадратных неравенств», обучающиеся должны получить необходимый объем знаний про то, что такое неравенство, свойства числовых неравенств, как решаются линейные неравенства. Презентации по данным темам имеются на данном ресурсе.
В самом начале презентации автор предлагает обучающимся познакомиться с понятием квадратных неравенств. Он определяет их, как неравенство вида ax2+bx+c>0, где a>0. Для того, чтобы научиться решать такие неравенство достаточно знать, как они выглядят. Поэтому автор тут же предлагает изучение способов решения рассматривать сразу на примерах. И первый такой пример демонстрирует, что нужно рассмотреть функцию, которая находится в левой части неравенства. Следует построить ее график. Так как задание подразделяется на четыре подпункта, и отличаются все эти неравенства только знаком, то достаточно для всех этих случаев одного графика. По нему теперь следует определять решения.
Для первого случая нужно найти все значения функции, которые принимают только положительные значения. На графике этому будут соответствовать все точки графика, которые лежат строго выше оси абсцисс. Для того, чтобы определить решения второго случая, необходимо рассматривать все точки графика этой функции, которые лежат строго ниже оси абсцисс. Так как знак неравенства строго меньше нуля. Третий случай отличается от первого только тем, что функция может принимать еще и значение нуль, поэтому к решению первого случая добавляется еще и нуль.
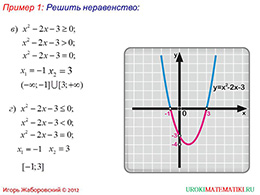
слайды 3-4 (примеры)
Аналогично и четвертый случай, который связан со вторым. Он имеет те же решения, включая нуль. На этом примере, как раз, автор показывает, как правильно записываются решения неравенства в разных случаях. то есть в каком случает скобка круглая, в каком квадратная.
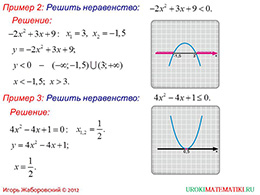
Далее второй пример, который показывает немного другой способ решения квадрантного неравенства. Здесь уже нужно построить график функции не в системе координат, а на прямой, где должны быть отмечены точки пересечения графика с осью абсцисс. А затем, глядя на знак неравенства, следует определять, какая часть графика требуется в качестве решений, которая лежит ниже или выше этой прямой. В данном случае берутся участки графика, которые лежат ниже прямой.
Поэтому интервал решений будет двойной. На этом же слайде имеется еще один пример, где показан случай, когда график не пересекает прямую, а только касается ее в одной точке. Но так как по условию знак стоит меньше или равно нуля, то должен выбираться участок, который расположен ниже прямой. Но таких участков нет, весь график лежит выше. Но так как в условии допускается равенство нулю, то единственным решением будет значение переменной, равное 0,5.

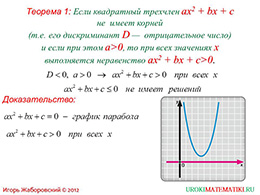
слайды 5-6 (алгоритм решения, теорема)
Далее автор приходит к алгоритму решения квадратных неравенств. Он состоит из трех пунктов. Согласно первому пункту, следует решить квадратное уравнение, приравняв квадратный трехчлен к нулю. Затем полученные корни отметить на прямой, которая является осью x, и от руки провести через эти точки параболу, учитывая направление ветвей. И затем по данной модели найти все решения неравенства.
И в завершении презентации автор предлагает рассмотреть теорему, которая связывает количество решений неравенства от знака дискриминанта трехчлена. Это значит, что при отрицательном дискриминанте при положительном первом коэффициенте неравенство ax2+bx+c, которое больше либо равно нулю, не имеет решений, а если больше нуля, то решения – все действительные значения переменной x.
Данная презентация может стать незаменимой деталью урока по теме «Решение квадратных неравенств». Но эта презентация является лишь первой частью. Поэтому следует продолжение данной темы. А найти презентацию, которая станет продолжением данной можно также у нас. По желанию учителя в презентацию можно добавить свои примеры.
| Автор | |
|---|---|
| Дата добавления | 31.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 5593 |
| Номер материала | 315 |