
Презентация "Взаимное расположение прямой и окружности"

Краткое описание документа:
Урок «Взаимное расположение прямой и окружности» окажется очень увлекательным, если его правильно подать. Благодаря структуре и подаче информации в презентации, эта тема воспримется очень легко и понятно. Пособие оформлено по всем стандартам, соответствует всем нормам, которые рекомендуются для подобных обучающих файлов.
Тема касается взаимному расположению геометрических объектов. Как известно, прямая может быть размещена на плоскости различными способами относительно некоторых других фигур. Рассмотрим, каким образом могут быть расположены прямая и некоторая произвольная окружность на плоскости.

слайды 1-2 (Тема презентации "Взаимное расположение прямой и окружности", пример)
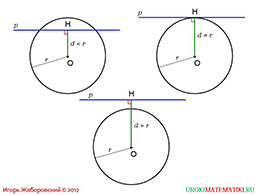
Прямая обозначается в презентации латинской прописной буквой p. Центр окружности – точкой О, радиус - r, а расстояние от центра окружности до прямой - d. Итак, на первом слайде мы видим три различных способов взаимного расположения прямой и окружности. В первом случае можно увидеть, что прямая пересекает окружность, но, при этом, не проходит через ее центр.
Для того, чтобы обозначить расстояние от точки О до прямой p необходимо опустить к прямой высоту, то есть отрезок, который составит с прямой 90 градусов. Обозначается на рисунке буквой d, прямой угол автором также отмечен. Мы видим, что данное расстояние меньше, чем радиус окружности. Дело в том, что прямая пересекает окружность в двух точках. Точка пересечения высоты, опущенной с центра окружности к прямой, обозначена буквой H.
слайды 3-4 (примеры)
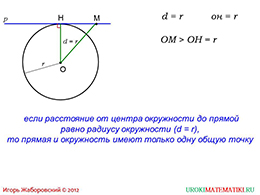
Рассмотрим второй случай. Здесь прямая p пересекает окружность, при этом «задевая» только одну точку. Опустив высоту от центра окружности к прямой, можно выяснить, что радиус и высота равны. Таким образом, можно сделать следующий вывод: если прямая пересекается с окружностью в одной точке, то расстояние от ее центра до прямой будет равен радиусу, и собственно говоря, являться им.
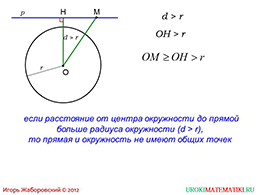
И, наконец, третий случай. Прямая не пересекается с окружностью ни в одной точке! Проведя длину, выяснится, что расстояние больше, чем радиус.
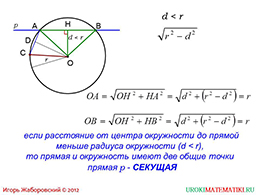
На следующем слайде даны выводы. Итак, когда расстояние между центром окружности и некоторой прямой оказывается меньше радиуса, то делаем вывод, что данная прямая имеет две общие точки с окружностью. Это можно доказать, проведя дополнительные построения. Автор получил треугольник, с проведенной высотой, ребрами которого являются радиусы. Алгебраическое доказательство приведено и при минимальных усилиях станет понятным для школьников.
слайд 5 (пример)
Следующий слайд рассматривает отдельно случай, когда прямая пересекает окружность только в одной точке. Было уже выяснено, что в этом случае расстояние и радиус окажутся равными. Алгебраические разъяснения также даются на этой странице.
На завершающем слайде подробнее рассматривается последний случай, когда прямая не пересекалась с окружностью ни в одной точке. Таким образом, зная лишь значение радиуса некоторой окружности и расстояние от ее центра до некоторой прямой, можно выяснить, пересекает ли прямая окружность, и, если да, то каким образом. Эти знания могут пригодиться при решении геометрических задач различного рода.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 5326 |
| Номер материала | 348 |