
Презентация "Объем конуса"

Краткое описание документа:
В пространственной геометрии существуют три фигуры в которых, при построении, используется окружность: цилиндр, шар и конус. Последняя из них сочетает в себе еще и такой элемент многоугольника, как угол. Эта презентация посвящена конусу, а также теореме, позволяющей рассчитать объем фигуры на основе имеющихся данных.
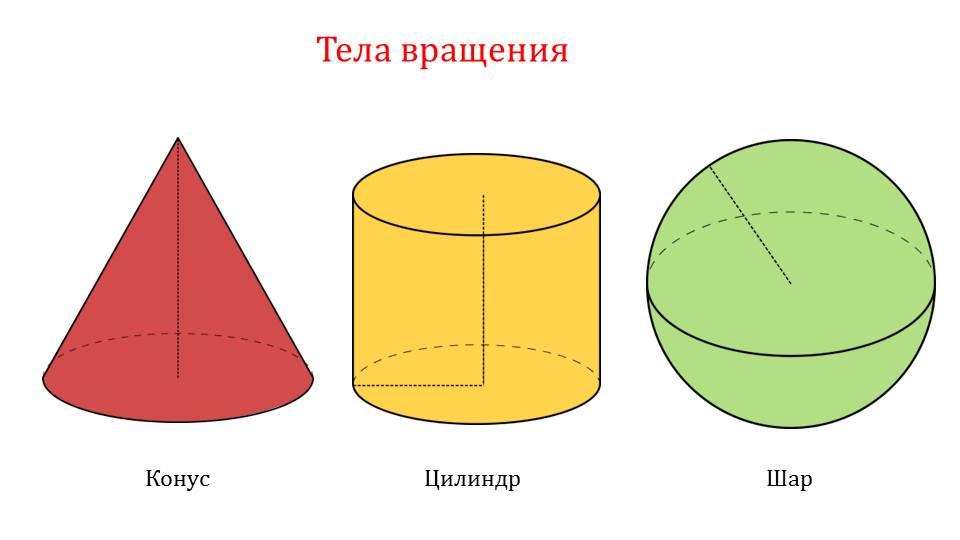
Учитывая специфику конуса, презентация построена не совсем обычно, так как ее первая часть заключается в ознакомлении с фигурой и повторением ранее изученного материала, необходимого для понимания, доказательства и практического применения теоремы «Объем конуса».
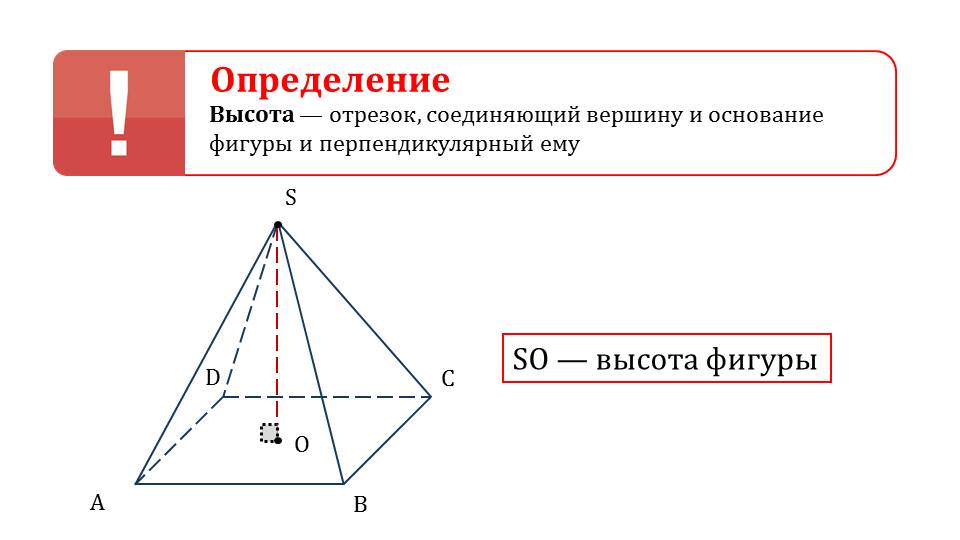
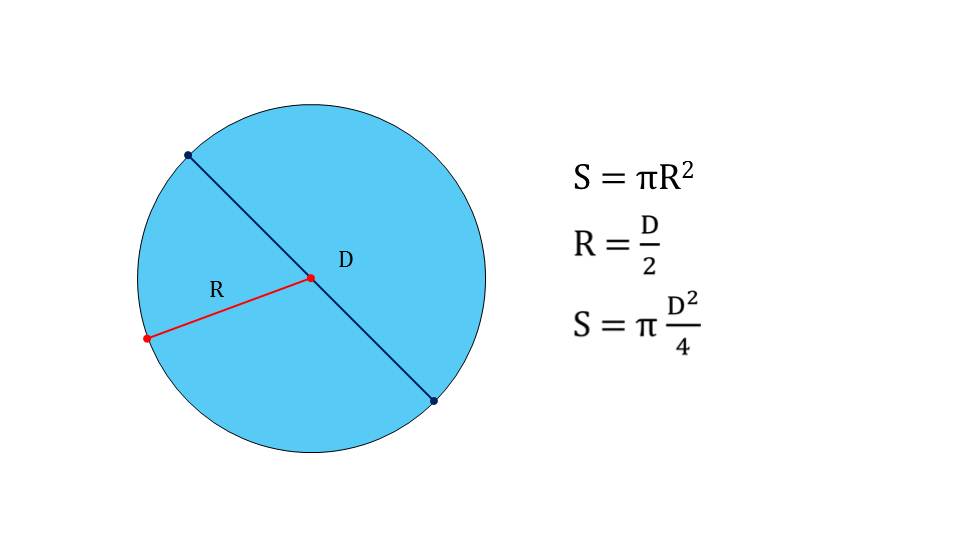
После презентации самой фигуры, а также ее фундаментальных отличий от цилиндра и шара, ученикам предлагается вспомнить понятие высоты в пространственной фигуре, в частности на примере пирамиды, а также восстановить свои познания из области планиметрии, которые касаются площади окружности, диаметра и радиуса.
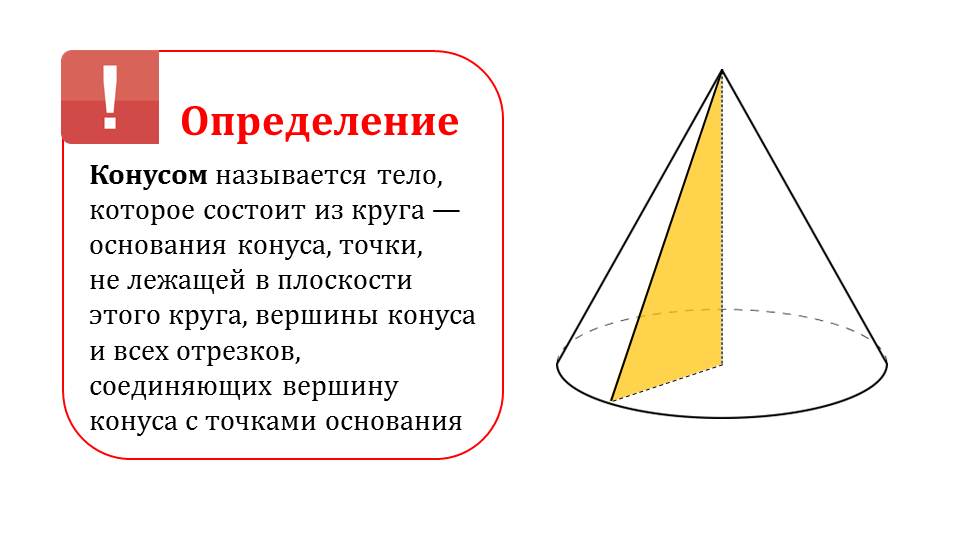
В следующей части урока даются теоретически знания: геометрическое определение конуса, а также теорема об объеме этой фигуры. Конус – фигура, состоящая из окружности и точки, распложенной в другой плоскости, но соединенной с основанием отрезками.
После изучения теоремы предлагается ознакомиться с ее доказательной базой, которая, в первую очередь, основывается на знаниях, повторенных в первой части презентации.
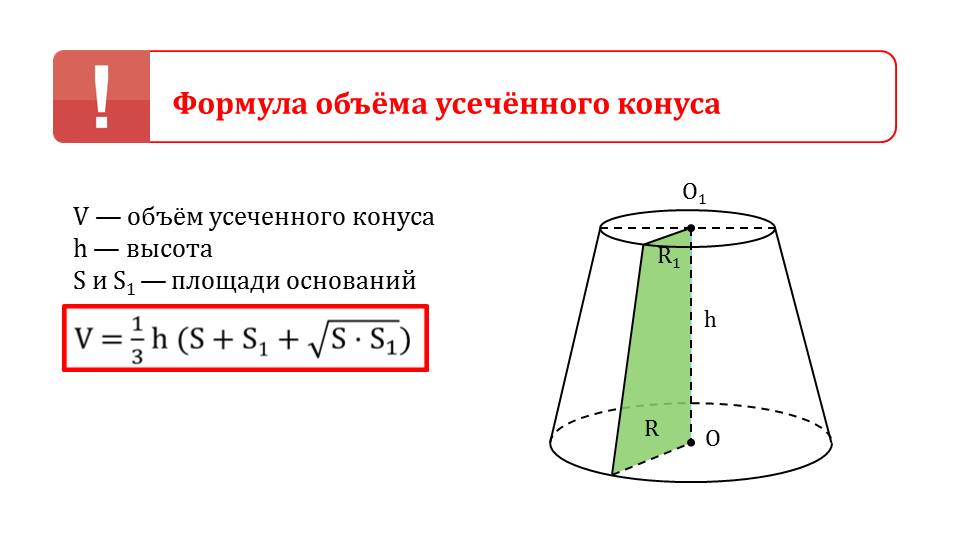
Геометрическая фигура конус может иметь еще один вид, о котором рассказывается в продолжении презентации. Усеченный конус состоит из двух окружностей, расположенных так, чтобы отрезки, соединяющие их в пространстве, в дальнейшем сходились в одной точке.
Для базового курса школьной программы требуется знать только формулу объема усеченной призмы, определение которой дается в следующей теореме.

Каждая теорема, формула и определение в презентации выделены более крупным шрифтом и обращают на себя внимание, благодаря красной рамке. Такой подход позволяет более эффективно воспринимать требуемый материал, позволяя ученику обучаться способности выявлять в тексте важную информацию.

Заключительная часть презентации отдана на решение и разбор двух тематических задач, позволяющих лучше понять теорию, чтобы применять ее в дальнейшем, на практике.
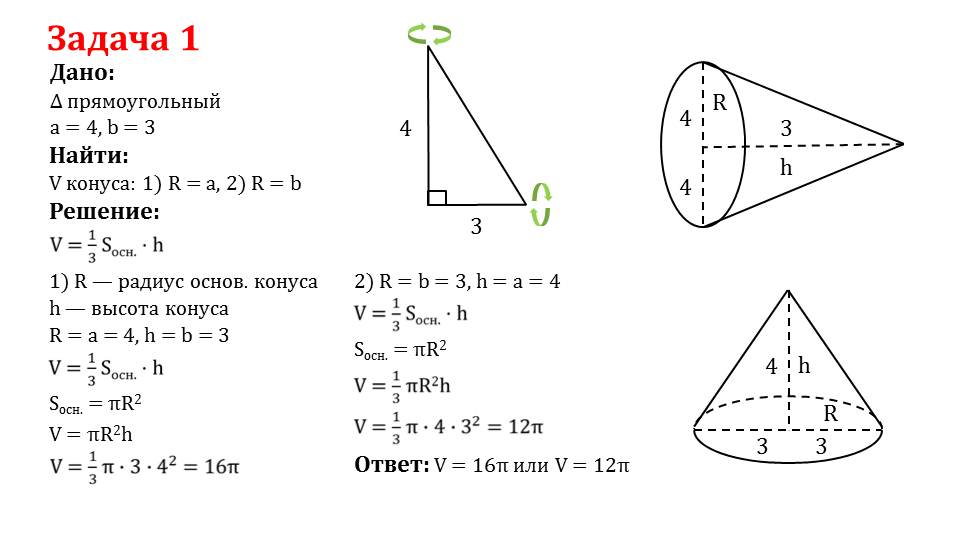
В первой задаче предлагается найти объем конуса, построенного на основе прямоугольного треугольника с известными, по условию значениями катетов. Само условие подразумевает применить метод дополнительного построения, для облегчения процесса решения.
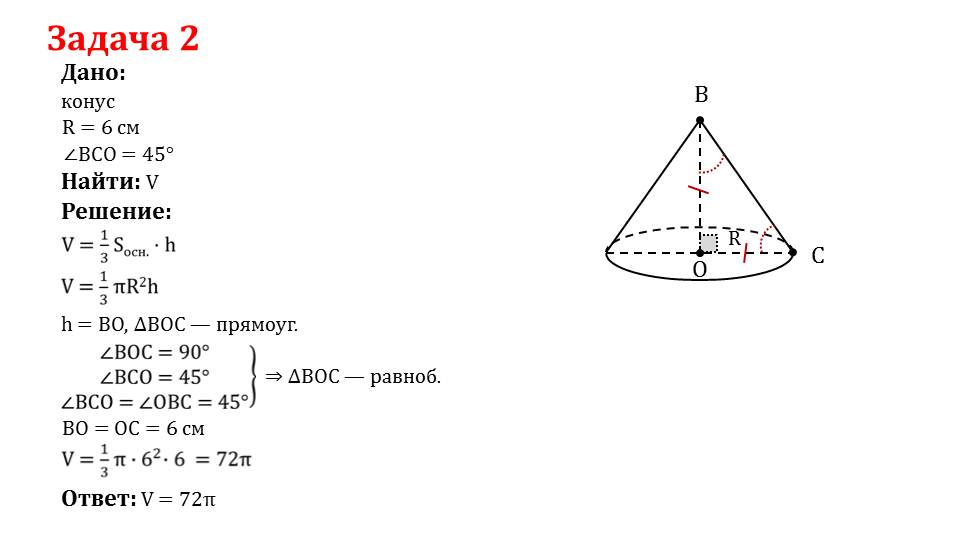
Вторая задача в своем решении требует дополнительного доказательства существования равнобедренного треугольника, построенного на основе высоты конуса, радиуса окружности и отрезка, соединяющего основание и вершину пространственной фигуры. Для этого потребуется вспомнить определение равнобедренного треугольника, которое тесно связано с понятием суммы всех углов этой фигуры. После предварительной работы, задача переходит в завершающую фазу, где необходимо найти объем конуса ,основываясь на полученных в процессе решения данных.
На самом деле, при всей своей уникальности, конус – одна из простейших пространственных геометрических фигур. Практические занятия, связанные с этой тематикой легки в понимании, особенно если использовать данную презентацию в качестве дополнительного материала при самостоятельной работе учеников в свободное время.
В отличие от изложения материала в школьном учебнике, презентация «Объем конуса» предлагает только необходимые сведения, расположенные в строго определенном порядке. Полное отсутствие ненужного материала, четкость определений и простота доказательств положительно влияют на запоминание и понимание материала учениками, что еще раз показывает высокую эффективность такого типа подачи информации.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 10225 |
| Номер материала | 984 |