
Презентация "Объем призмы"

Краткое описание документа:
Продолжим изучение объемов геометрических тел и рассмотрим в этой презентации тему вычисления объема призмы.
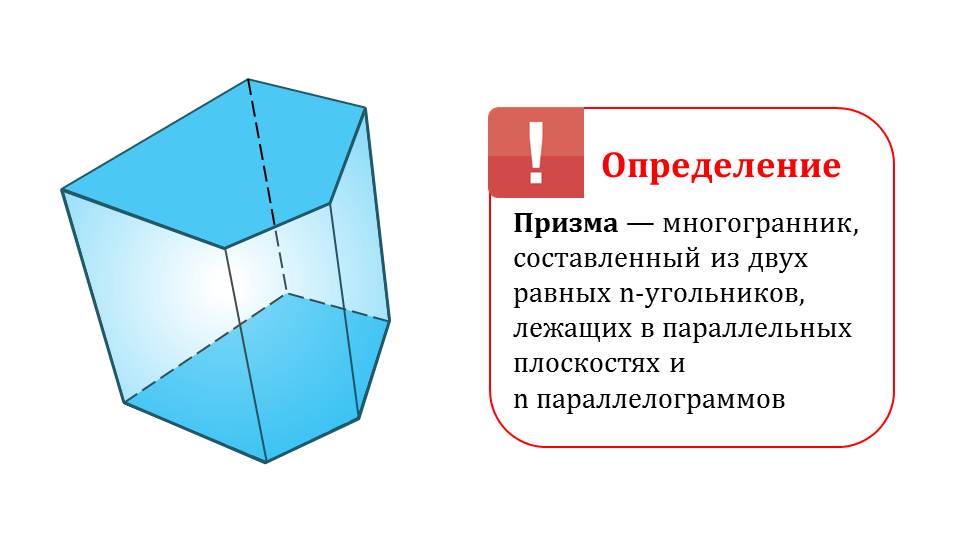
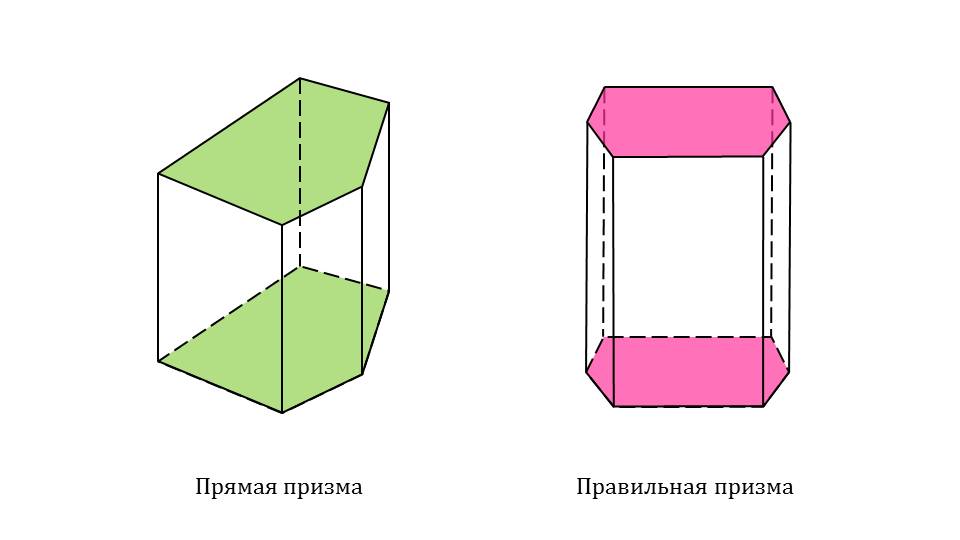
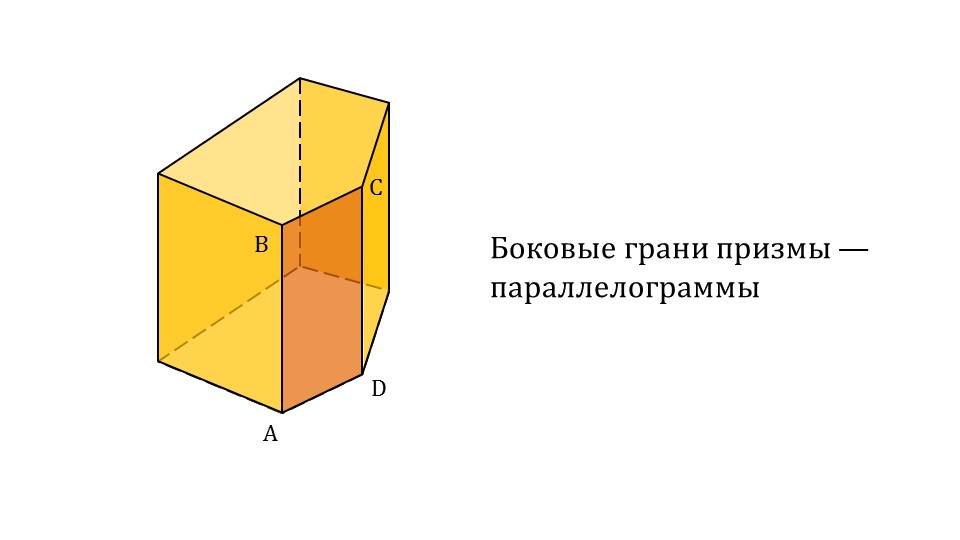
Для начала вспомним определение. Призма – это многогранник, который состоит из n-параллелограммов и двух равных n-угольников, находящихся в параллельных плоскостях. Изображение призмы представлено на рисунке. На следующем слайде показаны рисунки прямой и правильной призм. В прямой призме основания перпендикулярны боковым граням; в основании правильной призмы лежит правильный многоугольник. Боковые грани призмы являются параллелограммами (слайд 4).
Рассмотрим теорему: объем прямой призмы вычисляется умножением площади основания на ее высоту V = Sоснxh. Разберем доказательство теоремы.
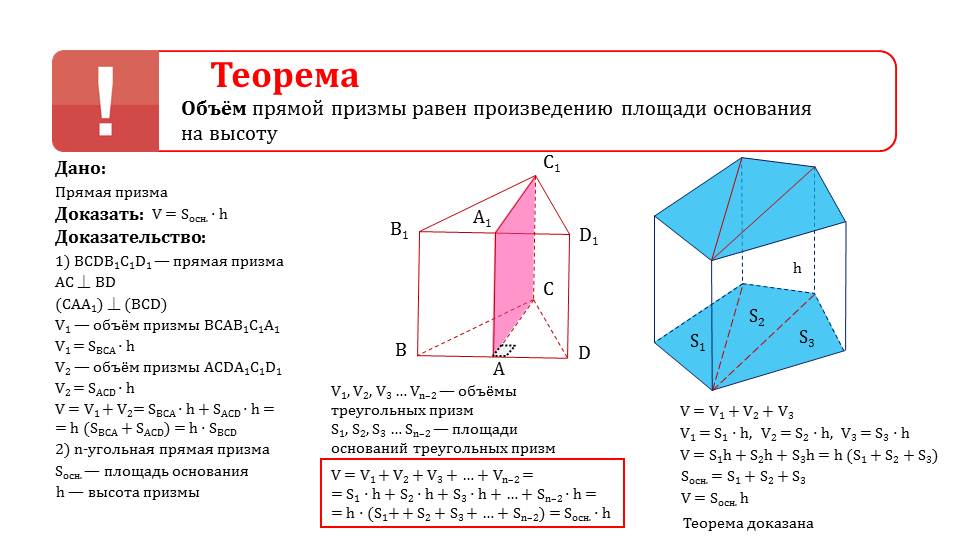
Дана прямая призма, обозначим ее как BCDB1C1D1. Проведем AC перпендикулярно BD, тогда плоскость CAA1 будет перпендикулярна плоскости BCD. Обозначим объем призмы BCAB1C1A1 как V1. Объем V1 = SBCAxh. А объем призмы ACDA1C1D1 обозначим как V2.Запишем, что V2 = SACDxh. Тогда объем исходной призмы будет равен V = V1 + V2 = SBCAxh + SACDxh = h (SBCA + SACD). Полученное выражение в скобках SBCA + SACD – это площадь основания исходной полной призмы. Запишем, что площадь основания Sосн = SBCA + SACD, тогда получим V = Sоснxh, что и требовалось доказать. В этом варианте доказательства мы рассмотрели прямую треугольную призму. При рассмотрении произвольной прямой призмы, в которой количество углов будет более трех, (например, пять) прибегнем к следующим действиям. Проведем через одно из боковых ребер диагональные плоскости (см. рисунок), исходная призма в таком случае разделится на три треугольные призмы. Объем исходной призмы будет равен сумме объемов этих треугольных призм V = V1 + V2 + V3. Объем первой треугольной призмы равен V1 = S1xh,объем второй V2 = S2xh, объем третьей V3 = S3xh.
Следовательно, V = S1xh + S2xh + S3xh= h (S1+ S2+ S3). Значение S1+ S2+ S3 это площадь основания исходной призмы. По-другому можно записать, что V = h (S1+ S2+ S3) = hxSосн.

Мы рассмотрели доказательство теоремы для прямой призмы, в основании которой лежит пятиугольник. Но теорема будет справедлива для любой прямой призмы. В таком случае обозначим объемы треугольных призм как V1, V2, V3 … Vn-2, а их площади оснований как S1, S2, S3 … Sn-2. Тогда будет справедливо выражение V = h (S1 + S2 + S3 + … + Sn-2).
Перейдем к решению задач. Задача 1. Даны четыре правильных n-угольных призмы, где в каждой призме известна длина ребра а. Основаниями призм являются многоугольники с количеством улов:
а) n = 3
б) n = 4
в) n = 6
г) n = 8
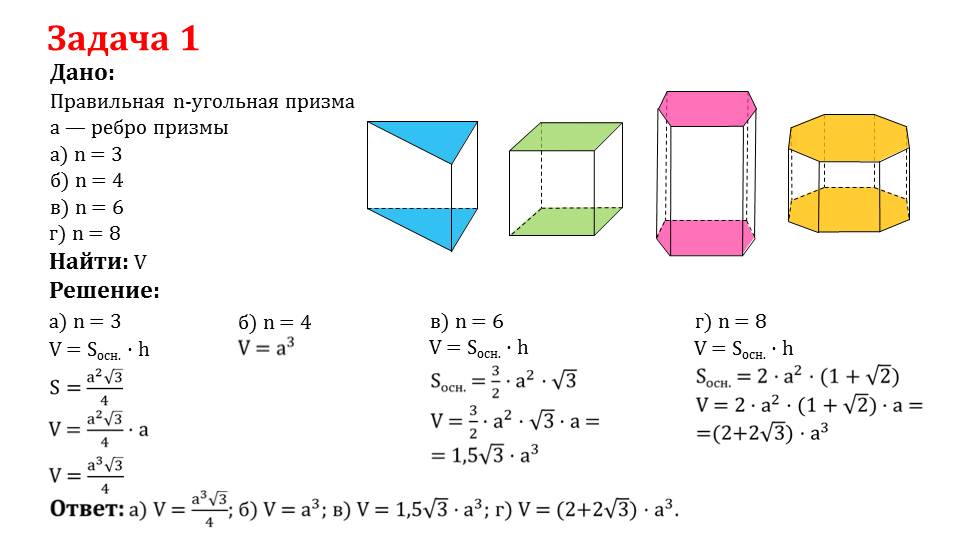
Нужно найти объем каждой призмы.Т.к. во всех вариантах длина ребра нам известна, то для решения применим формулу V = Sоснxh. В варианте а, в и г для вычисления площади основания Sосн применим уже известные нам формулы нахождения площади многогранников. В варианте б призма является кубом, поэтому его объем можно найти по формуле V = a3.
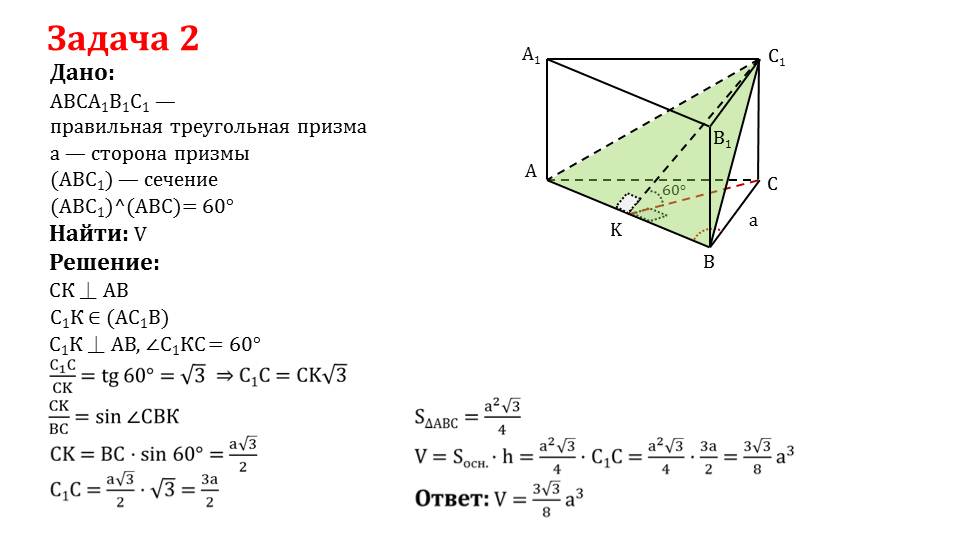
Задача 2. Дана ABCA1B1C1 – правильная треугольная призма, а – сторона призмы, ABC1 – сечение, угол между плоскостями ABC1 и ABC равен 60 градусов. Необходимо найти объем призмы. Для решения проведем CKперпендикулярно AB. Отрезок С1Kбудет принадлежать плоскости ABC1,
CKперпендикулярен AB, следовательно, мы можем найти значение угла C1KC. Далее найдем значение CK с помощью функции синуса. Тогда в треугольнике мы сможем вычислить сторону C1С. Таким образом, мы получили все данные для нахождения площади основания треугольника ABC. Зная площадь основания и высоту C1С, вычислим объем призмы.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 9722 |
| Номер материала | 979 |