
Презентация "Объем шара"

Краткое описание документа:
Презентации – довольно новый метод обучения, постепенно входящий в современный образовательный процесс. В отличие от обычного материала, изложенного в стандартном школьном учебнике, такой вид подачи информации более качественно справляется с возложенными на него обязанностями, так как очень часто включает в себя не только новые формулы, теоремы и теорию, но и предлагает по мере просмотра вспомнить уже пройденные разделы образовательного курса.
Презентация «Объем шара» наглядно демонстрирует уникальную геометрическую фигуру, в которой, при построении не используются прямые линии и углы, а также проводит знакомство учеников с теоремой и ее доказательством.
Теорема об объеме шара требует дополнительного построения на рисунке геометрической фигуры. В шаре необходимо прочертить окружность и радиус.

Сама доказательная база теоремы, взятая в красную рамку в презентации, для упрощения изучения разбита на четыре пункта. Первые два предлагают ученикам выполнить дополнительные построения, позволяющие в плотную подойти к логическому обоснованию формулы. Третья и четвертая часть доказательства теоремы – чистая математика ,где сначала аргументируется зависимость площади сечения от значения «х» (условно – высота образованного построениями усеченного конуса), а затем происходит окончательный расчет формулы объема шара.
Вторая половина презентации полностью посвящена разбору тематических задач, которые можно решать, используя приведенную и доказанную выше теорему. Знание и умение применять формулы объемов различных геометрических фигур очень важно, так как очень часто они используются в условиях реальной жизни, в строительной и пищевой сфере деятельности человека, а также на повседневном бытовом уровне. Понимание принципа расчета объемов различных фигур поможет избежать в жизни различных неприятных ситуаций, например, при отпуске продукции в обычном магазине. Именно поэтому умение оперировать и использовать известные данные очень важно в современном мире.

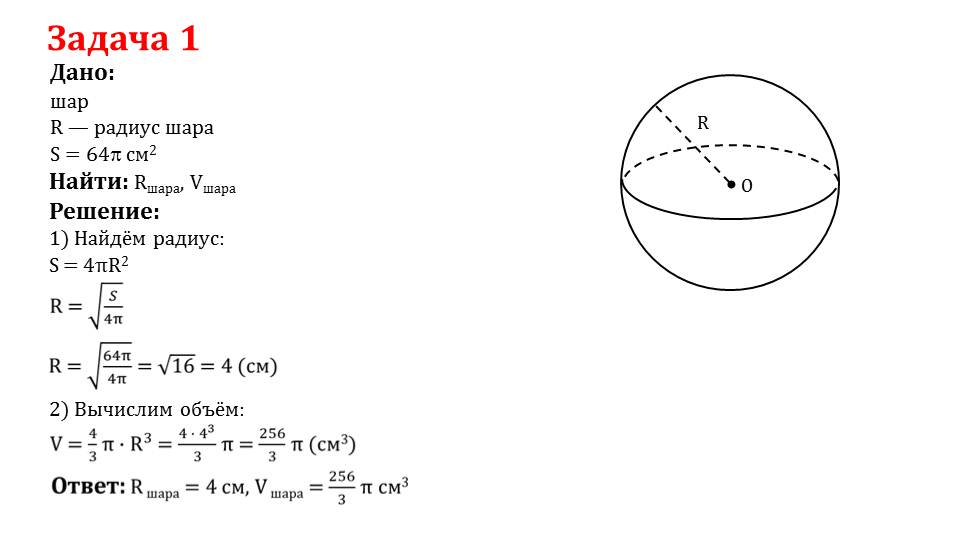
Первая задача довольно проста и требует нахождения объема и радиуса шара, зная площадь окружности, вписанной в данную геометрическую фигуру. Для решения поставленной задачи потребуется вспомнить формулу площади окружности, радиус которой равен радиусу шара. Найдя радиус, ученику, применив основную теорему из этой презентации, не составит труда подсчитать объем шара.
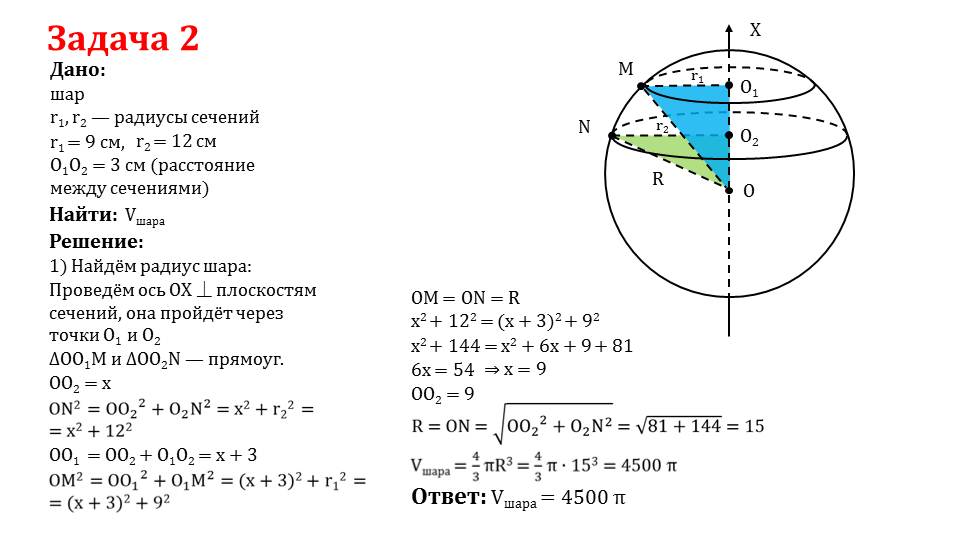
Вторая, предлагаемая к изучению, задача немного сложнее, требует дополнительного построения и полного понимания доказательства теоремы «Объем шара». Для решения задачи необходимо понять то, что полученные на рисунке треугольники – прямоугольные, гипотенузы которых равны между собой. Следующий шаг – применение теоремы Пифагора и решение нескольких чисто математических уравнений, позволяющих вычислить радиус шара. Заключение – применение формулы, которая была изучена в первой части презентации, и получение окончательного результата.
Наибольшей эффективности материал достигает тогда, когда информацию, предлагаемую в нем, легко усвоить среднестатистическому ученику.
Презентация «Объем шара» полностью выполнена с учетом этого фактора, основывается на общеобразовательном курсе средней школы, снабжена всеми необходимыми чертежами, а также доступным для понимания доказательством предложенной к изучению теоремы.
Самостоятельное ознакомление с презентацией не должно вызвать сложностей у учеников, хорошо знающий школьный курс геометрии. Применение этого материала во время проведения уроков в школе, гарантированно повысит интерес к уроку и значительно качественнее подготовит школьников к дальнейшей учебе.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 5488 |
| Номер материала | 985 |