
Презентация "Сфера. Площадь сферы"

Краткое описание документа:
Для того чтобы процесс обучения был более эффективным, нужно учитывать некоторые особенности восприятия информации человеком. Материал, представленный в виде мультимедийной презентации, значительно упрощает процесс восприятия информации. Это особенно актуально для молодых педагогов. При просмотре презентации задействуется зрительная память, благодаря чему материал усваивается быстрее. Презентации могут быть использованы учителями в качестве опорной информации для составления конспекта. Грамотно составленный и структурированный материал презентации позволяет постепенно и более эффективно овладевать информацией, затрачивая на это меньше времени и усилий.
В курсе изучения стереометрии, ученики 10 класса столкнутся с такой темой, как «Сфера. Площадь сферы». При ее изучении необходимо знать о том, что собой представляет это тело, какие основные характеристики он имеет.

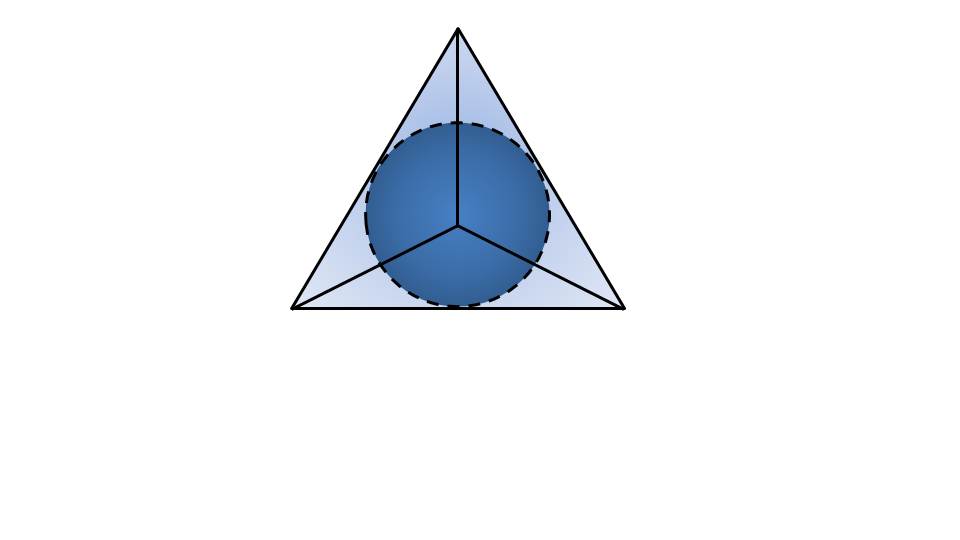
С этой информацией можно ознакомиться в предыдущих презентациях. Ученики должны уже уметь решать некоторые несложные и средней сложности задачи, знать, что такое радиус и другие параметры сферы.
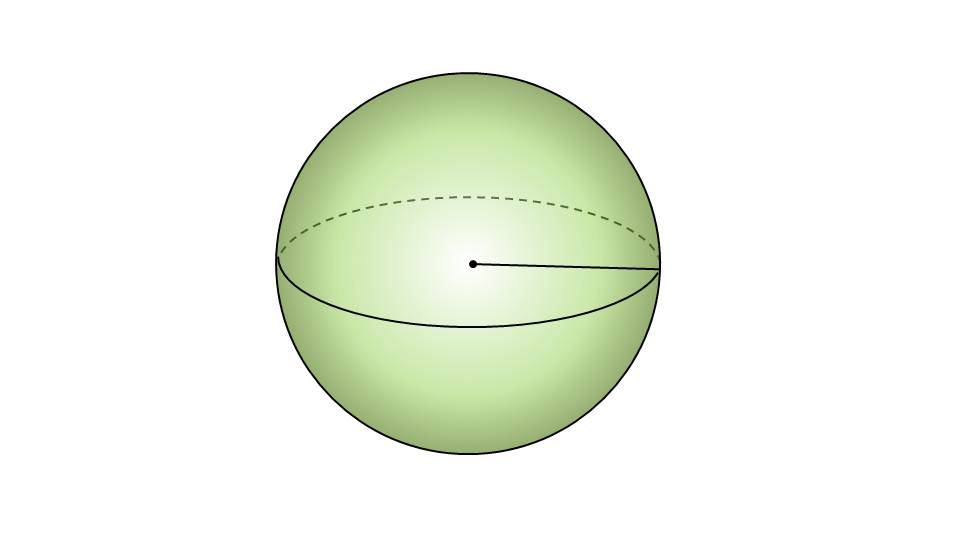
На первом слайде презентации демонстрируется сфера. Мы видим, что обозначен ее радиус.
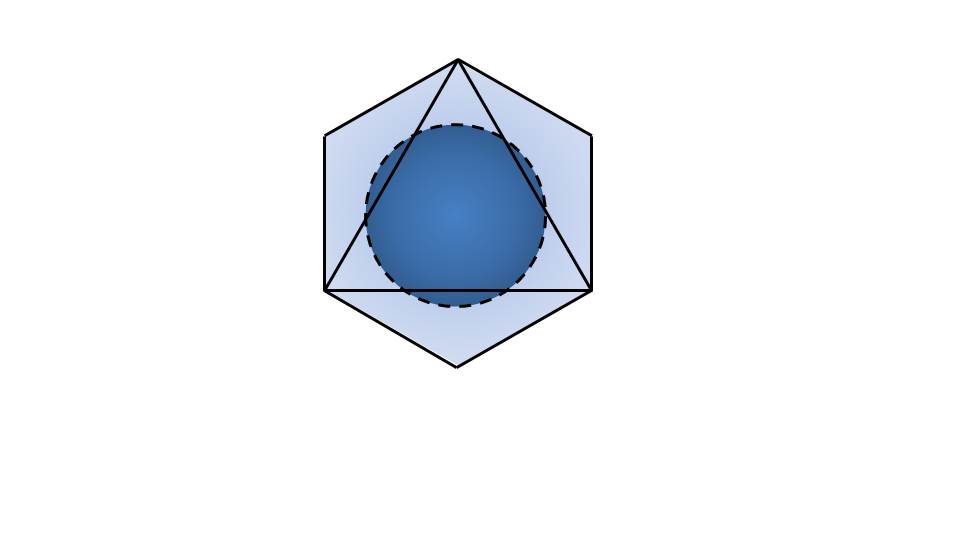
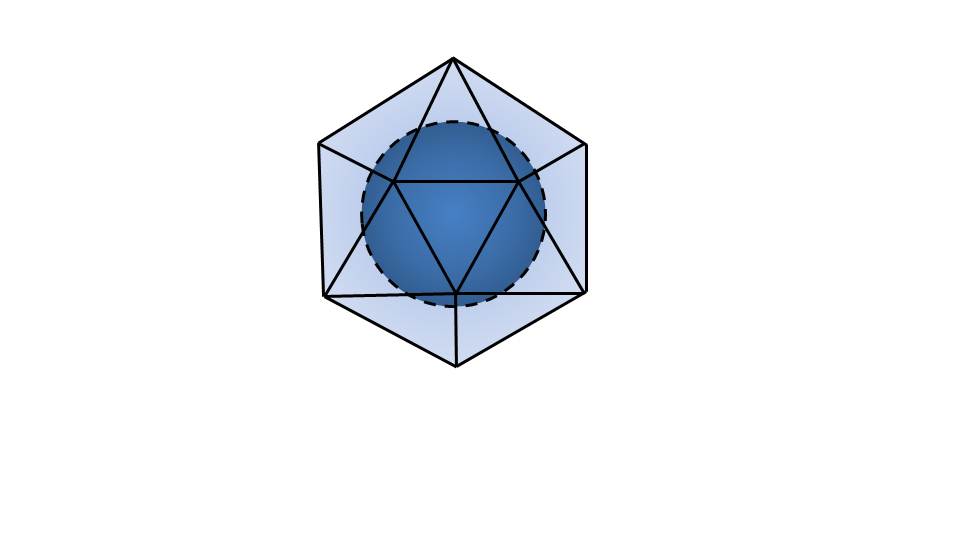
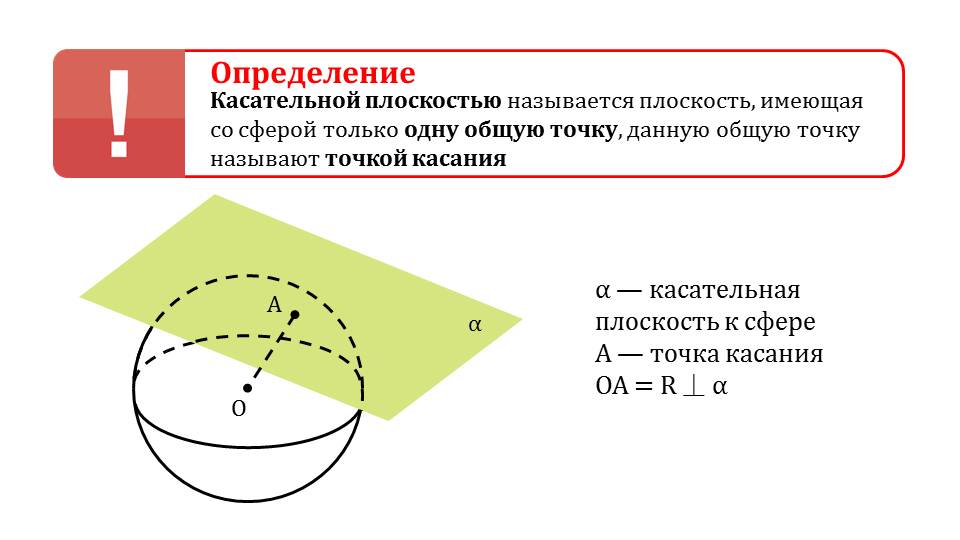
Далее напоминается, что же является касательной плоскостью к ней. На иллюстрации обозначены все параметры. Показывается, то плоскость альфа является перпендикулярной к радиусу.
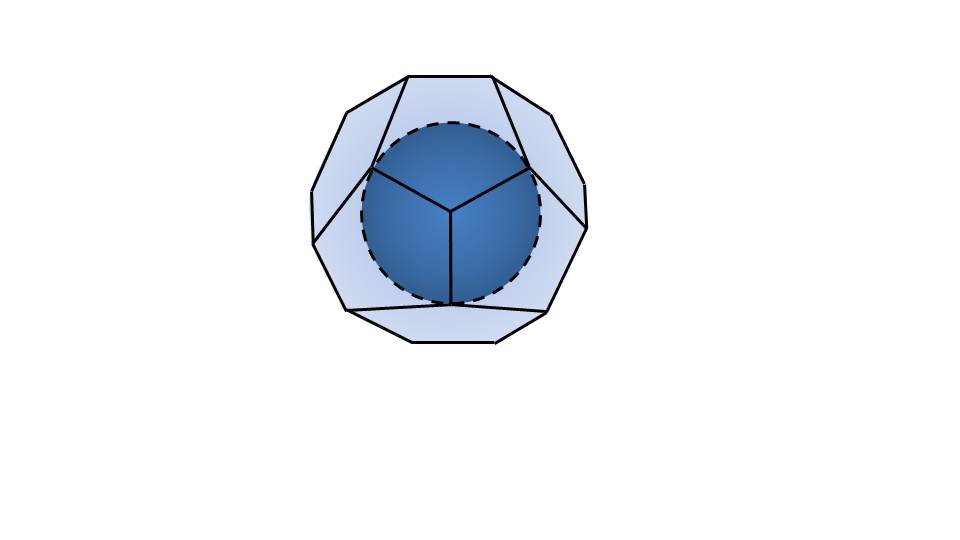
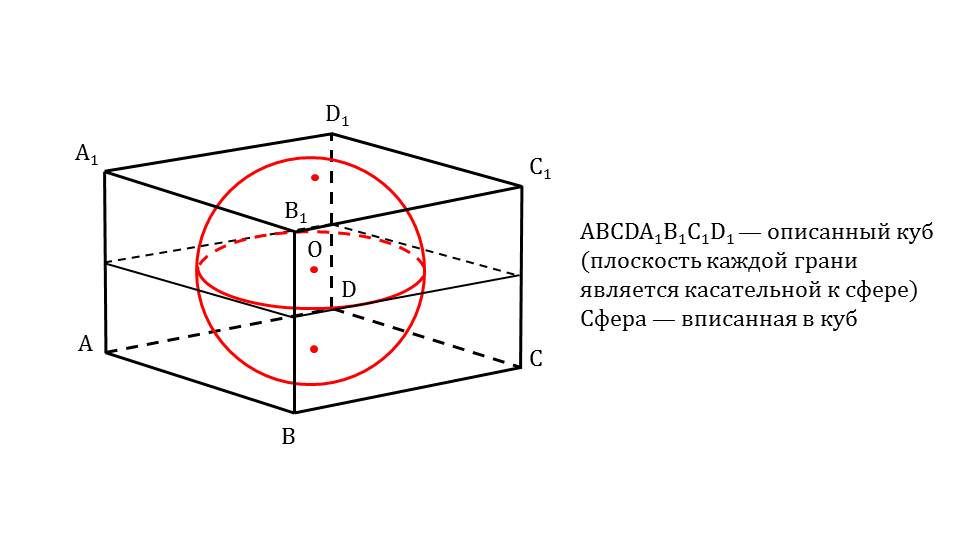
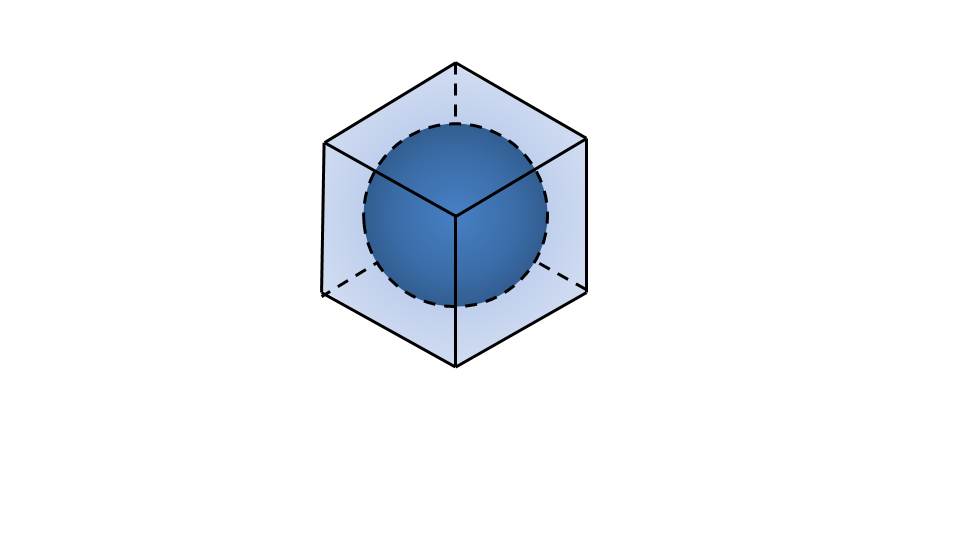
В следующем слайде рассматривается сфера, которая описана параллелепипедом. В этом случае, каждая грань будет являться касательной к сфере. В таком случае можно говорить, что сфера вписана в параллелепипед.
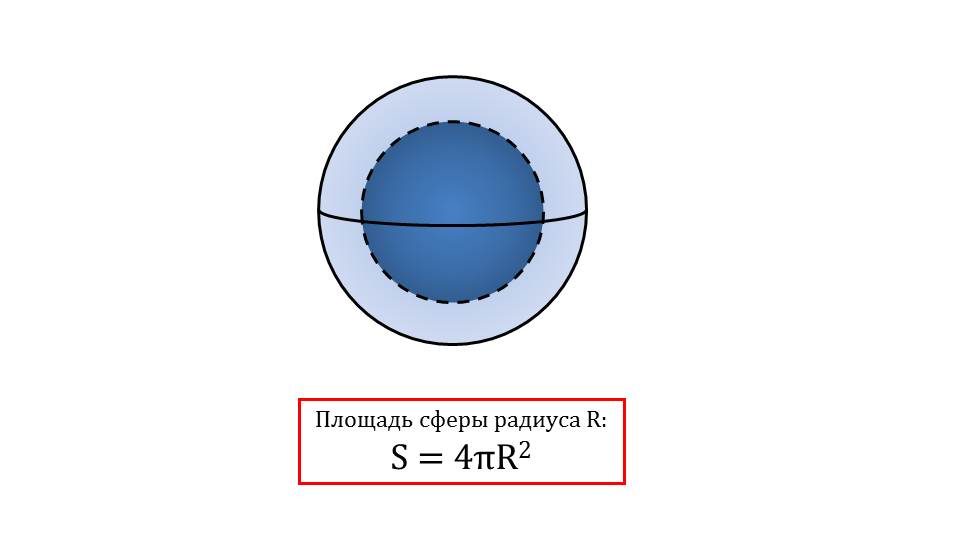
Далее приводится поэтапное объяснение получения формулы площади поверхности сферы.
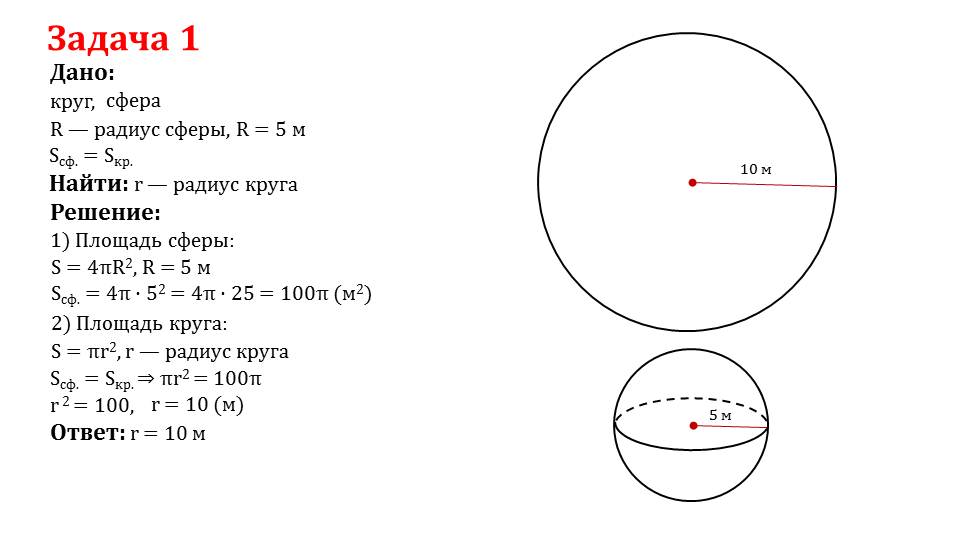
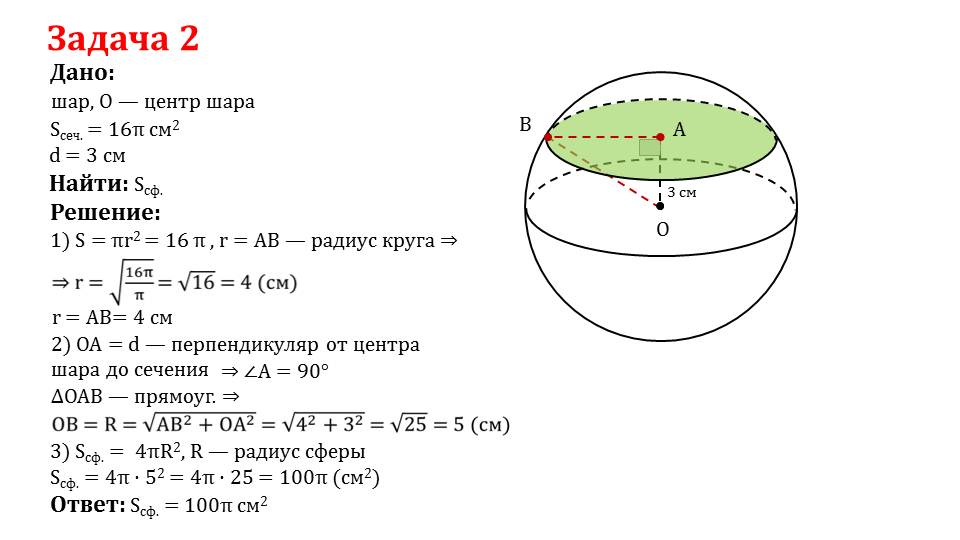
В заключительной части презентации приведены подробные решение некоторых задач. На основе их можно справиться с аналогичными задачами, которые могут быть заданы в качестве домашнего задания.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 6733 |
| Номер материала | 976 |